Тепловой баланс ректификационной колонны

Уравнение теплового баланса запишем согласно уравнению 5.32:

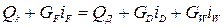
где Q_k – расход теплоты, получаемой кипящей жидкостью от конденсирующегося греющего пара в кубе-испарителе, Вт; Q_Д – расход теплоты, отводимый охлаждающей водой от конденсирующихся в дефлегматоре паров, Вт; G_F, G_D, G_W – массовые расходы питания, дистиллята, кубового остатка, кг/с; i_F, i_D, i_W – соответствующие удельные энтальпии, Дж/кг.

Рассчитаем расход теплоты в кубе – испарителе ректификационной колонны непрерывного действия по уравнению 5.34:

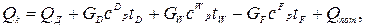
где с^D_р, c^W_р, c^F_р – средние удельные теплоемкости, Дж/(кг*К); t_D, t_W, t_F – соответствующие температуры, ^оС.

Для расчета расхода теплоты в кубе – испарителе, рассчитаем расход теплоты, отводимый охлаждающей воде в дефлегматоре по уравнению 5.35:

,

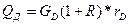где R – число флегмы; r_D – удельная теплота конденсации паров в дефлегматоре, Дж/кг.

Дальнейший расчет проведем, пренебрегая тепловыми потерями.

Приход тепла с сырьем при t_F = 81,8^oC рассчитываем по уравнению (5.51):

,

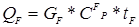где 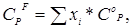x_i – массовая доля i – ого компонента в исходной смеси; С^о_Р – удельная теплоемкость i – компонента, Дж/(кг*К). Так как доля отгона равна нулю, то сырье поступает в колонну в кипящем состоянии.

Экспериментальные сведения о теплоемкости для многих веществ являются ограниченными. Поэтому прогнозирование теплоемкости оказывается неизбежным в большинстве практических расчетов. Поскольку речь идет о свойстве веществ в реальном состоянии, методы прогнозирования основаны на принципе соответственных состояний [22]. При массовых расчетах широко используется подход, основанный на разложении Питцера, которое для теплоемкости принимает вид:

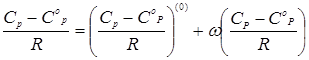, (5.64)

где ω – ацентрический фактор, 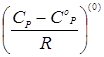- поправка к теплоемкости на давление, характеризующая поведение простого вещества, 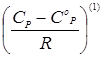- функция отклонения в поведении рассматриваемого вещества от поведения простого вещества, С^о_Р – идеально-газовая теплоемкость вещества при рассматриваемой температуре, С_Р – искомая теплоемкость, R – газовая постоянная, равная 8,31 Дж/(моль*К), или 1,987 кал/(моль*К).

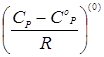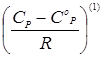Значения и представлены в таблицах Ли-Кеслера [22] как функции приведенной температуры и давления. Таблицы Ли-Кеслера составлены на основе уравнения состояния Бенедикта-Уэбба-Рубина с соблюдением общепринятых принципов, т.е. между любыми соседними значениями в столбцах или строках таблицы корректной является линейная интерполяция. В таблицах область, лежащая выше линии бинодали (в таблицах это жирная ломаная линия), принадлежит жидкому состоянию вещества, ниже – газообразному состоянию.

При прогнозировании теплоемкости ненасыщенных жидкостей хорошо зарекомендовали себя уравнения, предложенные Роулинсоном и Бонди (5.65), а также Штерлингом и Брауном (5.66):

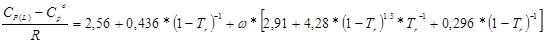(5.65)

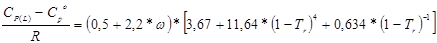, (5.66)

где С_P(L) – теплоемкость ненасыщенной жидкости при избранной температуре, С^о_Р – теплоемкость вещества в идеально-газовом состоянии при той же температуре, ω – ацентрический фактор, Т_r – приведенная температура, R – газовая постоянная, равная 8,31 Дж/(моль*К), или 1,987 кал/(моль*К).

Для теплоемкости насыщенной жидкости предложена корреляция Яна и Стила (5.67):

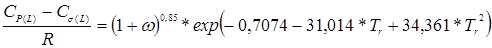, (5.67)

которая справедлива в интервале 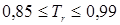. При температурах ниже T_r = 0,8 можно принять, что теплоемкость насыщенной жидкости (С_s(L)) примерно равна теплоемкости ненасыщенной жидкости С_P(L).

Приведем пример расчета теплоемкости бутана в зоне питания при температуре 81,8^оС и давлении в зоне питания - 2,75атм.

Так для бутана:

1. Идеально-газовая теплоемкость бутана С^о_Р при температуре 354,8 К из справочной литературы [10] равна 113,1 Дж/(моль*К).

2. Ацентрический фактор для бутана равен 0,19 [8].

3. Рассчитываем приведенные температуру и давление, зная критические температуру и давление для бутана: Т_с=425,2 К и Р_с =37,5 атм [8].

,

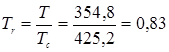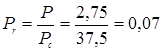
При температурах ниже T_r = 0,8 можно принять, что теплоемкость насыщенной жидкости (С_s(L)) примерно равна теплоемкости ненасыщенной жидкости С_P(L). Так как в нашем случае Т_r>0.8, то теплоемкость ненасыщенной жидкости найдем по уравнению Штерлинга – Брауна.

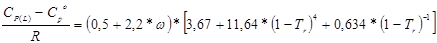
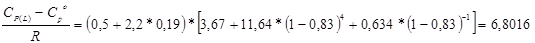
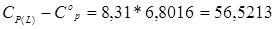
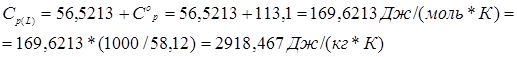
Так как для остальных компонентов в смеси приведенные температуры меньше 0,8, то для них расчет теплоемкости будем вести для состояния насыщенной жидкости. Результаты расчета приведены в таблице 5.15.

Таблица 5.15