Основные зависимости и расчетные формулы

1. Для расчета концентраций компонентов в ректификационных колоннах используют уравнение Дальтона и закон Рауля.

Концентрации компонента в газовой фазе может быть выражена через его парциальное давление. На основании уравнений Клайперона и Дальтона мольная (объемная) доля у любого компонента смеси идеальных газов равняется:

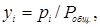(5.1)

где р_i – парциальное давление компонента газовой смеси; 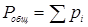- общее давление смеси газов или паров, равное сумме парциальных давлений всей компонентов.

Закон Рауля:

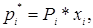(5.2)

где р_i^* - парциальное давление компонента в парогазовой смеси над жидкостью в условиях равновесия; Р_i – давление насыщенного пара чистого компонента – однозначная функция температуры; Р = f(t); x – мольная доля компонента в жидкости.

При подстановке в уравнение (5.2) значения 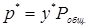из уравнения (5.1) получаем условие равновесия системы жидкость-газ:

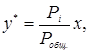(5.3)

где у^* - мольная доля компонента в парогазовой фазе, равновесной с жидкостью.

2. Уравнения материального баланса ректификационной колонны непрерывного действия:

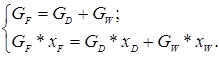
(5.4)

где G_F, G_D, G_W –массовые или мольные расходы питания, дистиллята и кубового остатка; x_F, x_D, x_w – содержание низкокипящего компонента (НКК) в питании, дистилляте и кубовом остатке, массовые или мольные доли.

Обычно в задании известно количество сырья, поступающего в питание колонны и содержание легколетучего компонента в питании, дистилляте и кубовом остатке (x_F, x_D, x_w). Решая систему уравнений (5.4), находим количество дистиллята и кубового остатка.

3. Температуры в кипятильнике и в верхней части колонны находим по следующим уравнениям:

для кипятильника (уравнение изотермы жидкой фазы)

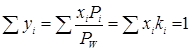(5.5)

для верхней части колонны (уравнение изотермы газовой фазы)

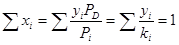, (5.6)

где Р_i – давление паров чистых компонентов при рабочей температуре; k_i – константа фазового равновесия i-ого компонента.

Константа равновесия индивидуального компонента определяется по уравнению: 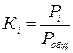, при Р_общ ≤ 5 ат. Если Р_общ >5 ат, то К = f(f_ж;f_п), где f - фугитивность

Расчет температуры в зоне питания зависит от доли отгона, которая находится из следующего уравнения:

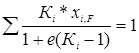, (5.7)

где К_i – константа фазового равновесия, е – доля отгона, x_i,F – мольная доля компонентов в питании.

Это уравнение используется при малых долях отгона е.

При больших долях отгона большую точность дает следующее уравнение:

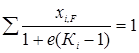(5.8)

Из уравнений (5.7) и (5.8) методом последовательных приближений, задаваясь долей отгона, можно найти температуру, с которой смесь входит в зону питания. Или, задаваясь температурой, определить долю отгона и соответственно составы паровой и жидкой фазы.

Давление паров чистых компонентов и К находят из справочной литературы [8] или по уравнению Антуана:

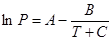, (5.9)

где Т – заданная температура, К; А, В, С – коэффициенты для индивидуального компонента [8,приложение А].

4. Для дальнейшего расчета необходимо знать физико-химические свойства веществ для найденных условиях (t и Р)_F,D,W. Это такие свойства как теплоемкость пара и жидкости (С_Р), теплота испарения жидкости и теплота испарения паров (r), плотность пара и жидкости (ρ), динамический коэффициент вязкости (μ). Для нахождения этих свойств можно воспользоваться справочными данными или найти их методами прогнозирования [8,9,10].

5. Минимальное число флегмы R_мин в ректификационной колонне непрерывного действия для идеальной смеси определяют по уравнению:

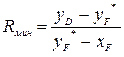, (5.10)

где у_D — мольная доля низкокипящего компонента в дистилляте; x_F — то же в исходной жидкости (питании) колонны; y^*_F — то же в паре, равновесном с жидкостью питания.

Рабочее (действительное) число флегмы:

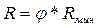(5.11)

Здесь φ > 1 – коэффициент избытка флегмы.

При расчетах ректификационных колонн рабочее число флегмы часто определяют по формуле [11]:

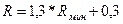(5.12)

6. Методы определения числа теоретических тарелок

Эти методы применимы для расчета как тарельчатых, так и насадочных колонн; различие появляется лишь при определении фактического числа тарелок или высоты насадки.