Данные для проверки температуры остаточного газа
| Компоненты | 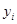
| К при 13,5 ат и -500С | 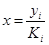
|
| Метан | 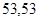
| 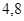
| 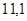
|
| Этилен | 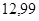
| 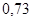
| 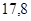
|
| Этан | 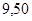
| 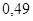
| 19,4 |
| Пропилен | 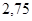
| 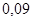
| 30,5 |
| ИТОГО | 78,8 | 78,8 |
Равенство 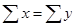 доказывает, что температура остаточного газа – 500С.
доказывает, что температура остаточного газа – 500С.
Определим температуру конденсата (табл.3.7)
Таблица 3.7
Определение температуры конденсата
| Компоненты | 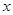
| К при 13,5ат и -150С | 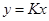
|
| Метан | 1,47 | 8,05 | 11,8 |
| Этилен | 2,01 | 1,7 | 3,4 |
| Этан | 2,5 | 1,2 | 3,0 |
| Пропилен | 8,25 | 0,33 | 2,7 |
| Углеводороды С4 | 7,00 | 0,064 | 0,4 |
| ИТОГО | 21,23 | 21,23 |
В результате расчета найдена температура конденсата tk = -15оС, определены составы конденсата и остаточного газа.
Контрольные задачи
Задача 3.1. Определить температуру кипения смеси приведенного состава (%, моль.) при соответствующем давлении:
| Вариант | |||||
| Давление, атм | |||||
| Состав, % моль. | |||||
| Бензол | |||||
| Циклогексан | |||||
| Гексан |
Задача 3.2. Определить температуру конденсации смеси паров следующего состава при давлении, приведенном в таблице.
| Вариант | |||||
| Давление, атм | |||||
| Состав, % моль. | |||||
| Бензол | |||||
| Циклогексан | |||||
| Гексан |
Задача 3.3. В прямоточный конденсатор поступает 100 кмоль/ч паров приведенного состава (%, об.).
Определить начальную температуру конденсации смеси при соответствующем давлении.
Определить количество и составы конденсата и остаточного газа при температуре на ΔТ градусов ниже начальной температуры конденсации смеси.
| Вариант | |||||
| Давление, атм | |||||
| Температура конденсации ΔТ | |||||
| Состав, % об. | |||||
| Водород | |||||
| Пропан | |||||
| Бутан |
Задача 3.4. Газ приведенного состава (%, об) подвергается конденсации в противоточном конденсаторе.
Определить начальную температуру конденсации смеси при соответствующем давлении.
Определить количество и составы конденсата и остаточного газа, если на конденсацию поступает 80 кмоль/ч паров, конечная температура остаточного газа T.
| Вариант | |||||
| Давление, атм | |||||
| Температура остаточного газа, Т | |||||
| Состав, % об. | |||||
| Водород | |||||
| Пропан | |||||
| Бутан |
4. Расчет реакторов
Основные зависимости и расчетные формулы
Основными задачами расчета реакторов для систем газ – твердый катализатор являются: определение объема катализатора, необходимого для достижения заданной степени превращения, определения высоты слоя катализатора, числа реакторов, диаметра труб или эквивалентного диаметра межтрубного пространства.
Для достижения определенной степени превращения, реагирующие вещества должны находиться в реакторе определенный промежуток времени, который обусловлен скоростью химической реакции, которая для каталитических реакций находится в сложной зависимости от кинетических и диффузионных факторов.
Кроме того, реакции протекают с определенными тепловыми эффектами, а в реакторе необходимо поддерживать температуру, близкую к оптимальной. Поэтому конструкция реактора должна обеспечивать надежный теплообмен.
Из сказанного следует, что для обоснованного вычисления основных размеров реактора необходимо совместное решение уравнений кинетики, диффузии, теплопередачи и гидродинамики.
Подобные расчеты достаточно сложны и требуют большого экспериментального материала не всегда доступного в настоящее время. Поэтому сохраняют свое значение и более простые, приближенные методы, позволяющие в ряде случаев оценить размеры реакторов:
- расчеты на основе определения высоты реакционной зоны;
- расчеты на основе вычисления времени контакта.
Расчет реакторов упрощенным методом
В.Б. Фальковского [3]
В.Б. Фальковский рассмотрел вопросы расчета реакторов, работающих в различных условиях теплообмена.
Адиабатические реакторы для процессов, протекающих в кинетической области
В интервале изменения температур в зоне реакции Δt=±25о с достаточной для технических расчетов точностью можно допустить существование линейной зависимости между константой скорости реакции k и температурой t
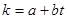 (4.1)
(4.1)
где а и b – постоянные.
Зависимость температуры реакционного газа t от степени превращения x выражается следующим уравнением (полученным из теплового баланса):
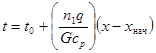 (4.2)
(4.2)
где t0 – начальная температура газовой смеси; n1 – начальное число молей реагирующего вещества (определяющего компонента), подаваемого в единицу времени в реактор; q – средний тепловой эффект реакции (со знаком минус при эндотермической реакции); G – массовая скорость газовой смеси; cp – средняя теплоемкость смеси реагентов; x – конечная степень превращения; xнач – начальная степень превращения.
Производя подстановку выражения для t из (4.2) в (4.1), а затем полученного преобразованного (4.1) в дифференциальные кинетические уравнения реакции, после интегрирования при xнач=0 получаются уравнения зависимости степени превращения x от высоты слоя катализатора Н (таб. 4.1).
Подобным же путем могут быть получены уравнения для случаев, когда xнач≠0. Эти зависимости необходимы при расчете многоступенчатых реакторов.
Реакторы с теплообменной поверхностью, имеющей постоянную температуру по высоте катализаторного слоя (охлаждаемые кипящей жидкостью или нагреваемые конденсирующимся паром)
При постоянной температуре поверхности теплообмена по всей высоте слоя катализатора, тепловой баланс можно выразить для элементарного участка приближенным уравнением:
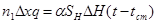 (4.3)
(4.3)
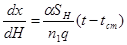 (4.4)
(4.4)
где 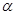 - коэффициент теплоотдачи от реагирующего газа к стенке;
- коэффициент теплоотдачи от реагирующего газа к стенке;
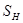 - удельная поверхность теплообмена на единицу высоты;
- удельная поверхность теплообмена на единицу высоты;
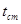 - температура стенки, практически равная температуре кипящего или конденсирующегося теплоносителя.
- температура стенки, практически равная температуре кипящего или конденсирующегося теплоносителя.
Уравнения (4.3) и (4.4) справедливы тогда, когда тепло, используемое на изменение температуры реакционного газа, незначительно по сравнению с теплом, которое передается через стенку, и температурный градиент в поперечном сечении контактного слоя невелик.
Решая (4.4) с основными дифференциальными кинетическими уравнениями необратимых реакций, В.Б. Фальковский получил зависимости температуры реакционного газа от степени превращения. После подстановки этих зависимостей в (4.1) и интегрирования были получены зависимости степени превращения от высоты контактного слоя (таб. 4.2).
Реакторы, охлаждаемые или нагреваемые внешним движущимся теплоносителем
Зависимость между температурой прямоточнодвижущегося внешнего теплоносителя и степенью превращения, если тепло, идущее на нагрев самого реакционного газа незначительно, описывается уравнением, аналогичным (4.4):
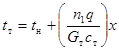 (4.5)
(4.5)
где tн, tт – температура теплоносителя в начале контактной зоны и на участке со степенью превращения x соответственно; Gт – массовая скорость теплоносителя; ст – его теплоемкость.
Уравнение теплопередачи для элементарного участка:
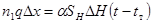 (4.6)
(4.6)
или
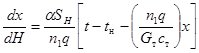 (4.7)
(4.7)
Решая уравнение (4.7) с основными дифференциальными кинетическими уравнениями реакций, можно установить зависимости температуры реакционного газа от степени превращения для соответствующих реакций. После подстановки последних в линейное уравнение константы скорости реакций и интегрирования получаются, как и в ранее описанных случаях, уравнения, связывающие степень превращения и высоту контактного слоя (табл. 4.3).
Рассмотренные выше закономерности и уравнения действительны только в тех случаях, когда питание реактора температуру, отвечающую расчетной температуре реакций. На практике это условие часто не соблюдается, и реагирующий газ поступает в аппарат с перегревом или недогревом. В этих случаях необходимо комбинировать различные варианты расчета. Так, если исходные реагенты имеют температуру ниже реакционной (при экзотермической реакции), то начальная зона реактора – до того момента, когда температура достигнет заданной, должна быть рассчитана (приближенно), как в случае адиабатических реакторов.
Пример 4.1. Рассчитать трубчатый контактный аппарат для экзотермической реакции, тепло которой отводится кипящей водой.
Исходная смесь подается в количестве G = 1030 кг/ч, в том числе 5 кмоль/ч основного реагента. Необходимо достигнуть степени превращения 0,84. Температура исходной смеси t0=135оС, температура t в зоне реакции не должна превышать 155оС.
Тепловой эффект реакции q=44600 ккал/кмоль.
Физические свойства реакционной смеси в условиях процесса: средняя теплоемкость cp=2,28 ккал/кг·град; динамическая вязкость μ=0,01 сп; средний размер зерен катализатора dз=7 мм.
Реакция протекает по кинетическому уравнению первого порядка без существенного изменения объема реакционной смеси (β=0). Константа скорости реакции k при 135оС равна 3,82 кмоль/м3·ч, а при 150 оС – 7,65 кмоль/ м3·ч.
Решение. Определим ориентировочно объем катализатора Vр, считая, что процесс проходит при постоянной температуре 150оС. Согласно кинетическому уравнению реакции первого порядка (таб. 4.1):
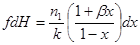
при β=0 после интегрирования
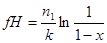
или
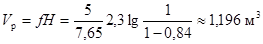
Полученное ориентировочное значение объема катализатора позволяет выбрать размеры трубчатки.
Принимаем аппарат с числом трубок n=211, внутренний диаметр которых равен 33 мм. Катализатор загружается в трубки. Высота заполнения
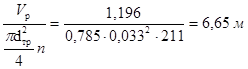
Для определения температурных перепадов в контактной зоне, находим значения коэффициентов линейного уравнения константы скорости реакции 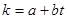 из двух уравнений
из двух уравнений
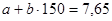
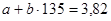
откуда a=-30,65; b=0,255.
При максимально допустимом повышении температуры реагентов со 135 до 155оС в начальной зоне, рассматриваемой приближенно как «адиабатическая», степень превращения составит при xнач=0 по (4.2):
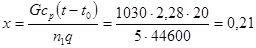
Максимальной температуры реакционная смесь достигнет в момент, когда тепло, выделяемое реакцией, сможет полностью отводиться через теплообменную поверхность, благодаря созданию достаточного температурного напора. В этом случае зависимость температуры реагентов от степени превращения при β=0 выражается уравнением (табл. 4.2):
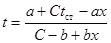
Подставляя в этом уравнении значения x=0,21 и t=155оС, находим искомую температуру стенки:
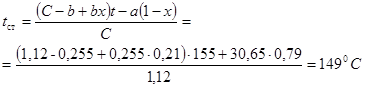
Этой температуре соответствует давление насыщенного пара 4,8 ат.
Значение коэффициента С в этом уравнении найдено по формуле (табл. 4.2)
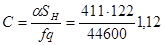
при этом
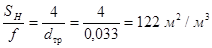
Коэффициент теплоотдачи от контактируемой смеси к стенке найден по известной формуле Кольборна:
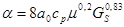
где cp – теплоемкость смеси, ккал/кг·град; μ – вязкость газа, сп; GS – удельная массовая скорость газа (на полное сечение трубы) кг/м·сек.
Коэффициент а0 зависит от отношения размеров зерна катализатора dз и диаметра трубы dтр:
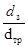
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 |
| а0 |
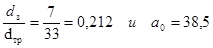
Следовательно
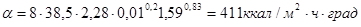
где
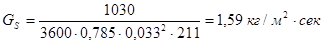
( 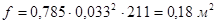 - площадь сечения труб).
- площадь сечения труб).
Высота «адиабатической» зоны находится по уравнению (таб. 4.1) при β=0
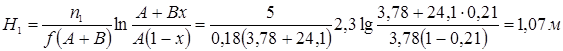
где 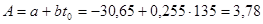 ;
;
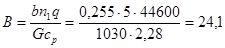
Высота зоны реакции для достижения степени превращения от 0,21 до 0,84 определяется из уравнения (таб. 4.2)
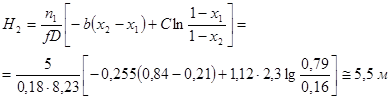
где 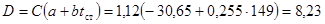
Общая высота контактного слоя составит: 1,07+5,5=6,57 м. Принимаем 7 м. Температура реакционной смеси на выходе из катализаторного слоя равна:
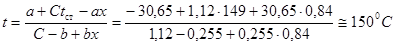
Расчет реакторов на основе вычисления
времени контакта
Для обратимой реакции общего вида
a1A1 + a2A2 + … Û a1/A1/ + a2/A2/ + …
объем реактора может быть найден из уравнения
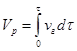 (4.8)
(4.8)
гдеVp – объем реактора (реакционной зоны);
vг – объемная скорость газа, проходящего через аппарат;
t - время контакта.
Для решения уравнения (4.8) необходимо знать вид функции
vг= f (x) и t = f / (x, t), где x – степень превращения, а t – температура реакции. Если реакция идет без изменения объема или при незначительном его изменении, что встречается довольно часто, уравнение (4.8) можно записать в виде
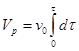 (4.9)
(4.9)
где v0 – начальная объемная скорость газа. В этом случае задача сводится к определению dt, то есть вида функции t = f / (x, t).
Существуют два метода расчета: графический Г.К. Борескова и аналитический М.Ф. Нагиева.
Расчет объема реакционной зоны графическим методом
Г.К. Борескова
Объемная скорость газа, проходящего через катализатор при степени превращения х, равна
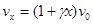 (4.10)
(4.10)
где 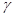 - относительное увеличение объема реакционной смеси при полном превращении
- относительное увеличение объема реакционной смеси при полном превращении
Таблица 4.1
Кинетические уравнения основных типов необратимых каталитических реакций для адиабатических условий при Δt=±25о
| Тип реакции | Кинетическое уравнение в дифференциальном виде (для изотермических условий) | Зависимость степени превращения от высоты контактного слоя |
| Реакция нулевого порядка | 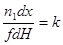
| 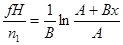 , где , где 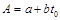 ; ; 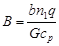
|
| Реакция первого порядка (слабая адсорбция реагента) | 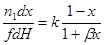
| 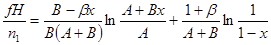
|
| Реакция с торможением продуктами реакции (реагент адсорбирует слабо, а продукт сильно) | 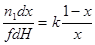
| 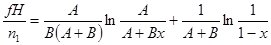
|
| Бимолекулярная реакция | 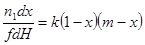
| 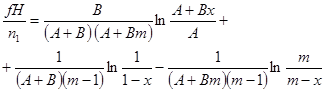
|
Примечание. f – сечение контактного слоя; β – разность стехиометрических коэффициентов конечных и начальных продуктов реакции; m – относительное количество молей второго компонента по отношению к первому, принятому за единицу
Таблица 4.2
Кинетические уравнения основных типов необратимых гетерогенных реакций в случае теплообменной поверхности, имеющей постоянную температуру по высоте катализаторного слоя
| Тип реакции | Зависимость температуры* реакционного газа от степени превращения для интервала Δt=±25о | Зависимость степени превращения от длины катализаторного слоя |
| Реакция нулевого порядка | 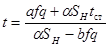
| 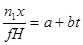
|
| Реакция первого порядка | 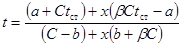 где
где 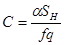
| при β=0 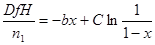 где
где 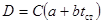
|
| Реакция с торможением продуктами реакции | 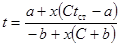
| 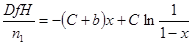
|
| Бимолекулярная реакция | 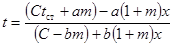
| 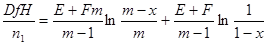 где
где 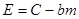 , ,
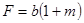
|
* При эндотермических реакциях тепловой эффект q берется со знаком минус.
| Тип реакции | Зависимость температуры реакционного газа от степени превращения | Зависимость степени превращения от длины контактного слоя |
| Реакция нулевого порядка | 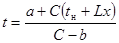 где
где 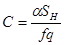 ; ; 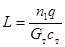
| 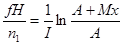 где где 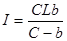 , , 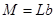
|
| Реакция первого порядка без изменения объема | 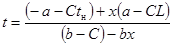
| 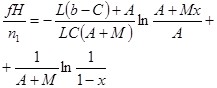
|
| Реакция с торможением продуктами реакции | 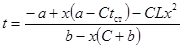
| 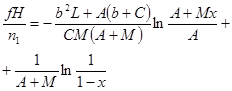
|
| Бимолекулярная реакция с избытком второго реагента | 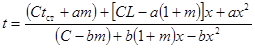
| 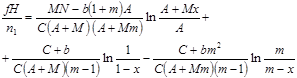 где
где 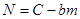
|
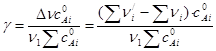 (4.11)
(4.11)
где 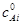 - начальная концентрация вещества Аi.
- начальная концентрация вещества Аi.
Тогда
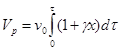 (4.12)
(4.12)
Если объем реакционных газов постоянен, то объем реактора находится из уравнения (4.9). Так как скорость реакции может быть представлена как функция степени превращения и температуры:
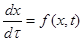 (4.13)
(4.13)
откуда
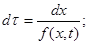
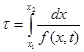 (4.14)
(4.14)
Для решения (4.14) должна быть дополнительно задана зависимость температуры от степени превращения 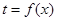 .
.
Эта зависимость определяется условиями теплообмена в процессе контактирования. Если эти условия известны, то уравнение (4.14) дает однозначное решение. Определение 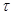 по уравнению (4.14) производится методом графического интегрирования с помощью диаграммы
по уравнению (4.14) производится методом графического интегрирования с помощью диаграммы 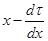 .
.
Как известно тепловой процесс можно рассматривать как изотермический, адиабатический или процесс с теплообменом с внешней средой.
Изотермический процесс
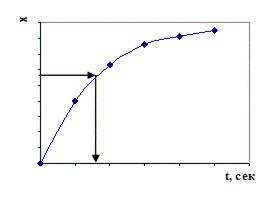
В этом случае величина 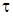 , согласно уравнению (4.14) , равна площади, ограниченной соответственно изотермой, осью абсцисс и ординатами x1 и x2 (рис. 4.1).
, согласно уравнению (4.14) , равна площади, ограниченной соответственно изотермой, осью абсцисс и ординатами x1 и x2 (рис. 4.1).
Если экспериментальные данные представлены в виде кривых t–x, то в построении диаграммы 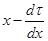 нет необходимости, так как значения
нет необходимости, так как значения 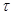 могут быть найдены непосредственно по заданным кривым (рис 4.2).
могут быть найдены непосредственно по заданным кривым (рис 4.2).

| 
|
| Рис. 4.1. | Рис.4.2. |
Адиабатический процесс
При адиабатическом ведении процесса (отсутствие теплообмена с окружающей средой), в случае экзотермической реакции температура реакционного газа непрерывно повышается с увеличением степени превращения, а в случае эндотермической реакции - понижается.
Изменение температуры со степенью превращения определяется уравнением теплового баланса
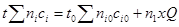 (4.15)
(4.15)
где 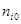 и
и 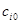 - число молей и молярная теплоемкость компонентов реакционной смеси до начала реакции;
- число молей и молярная теплоемкость компонентов реакционной смеси до начала реакции;
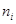 и
и 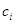 - число молей и молярная теплоемкость компонентов реакционной смеси, при степени превращения x;
- число молей и молярная теплоемкость компонентов реакционной смеси, при степени превращения x;
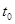 - начальная температура реакционной смеси, 0С;
- начальная температура реакционной смеси, 0С;
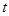 - температура реакционной смеси при конверсии
- температура реакционной смеси при конверсии 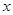 , 0С;
, 0С;
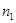 - число молей компонентов А1 в исходной смеси;
- число молей компонентов А1 в исходной смеси;
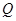 - теплота реакции на один моль компонента А1 (для экзотермической реакции положительная, а для эндотермической – отрицательная величина).
- теплота реакции на один моль компонента А1 (для экзотермической реакции положительная, а для эндотермической – отрицательная величина).
Если изменения теплоемкостей с температурой и степенью превращения, а также теплоты реакции с температурой невелики, то изменение температуры определяется линейным соотношением:
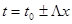 (4.16)
(4.16)
где 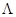 - коэффициент, зависящий от начального состава газовой смеси и равный изменению температуры при полном превращении. Таким образом, изменение температуры в зависимости от степени превращения изображается на графике
- коэффициент, зависящий от начального состава газовой смеси и равный изменению температуры при полном превращении. Таким образом, изменение температуры в зависимости от степени превращения изображается на графике 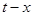 прямой, пересекающей ось ординат в точке t0. Тангенс угла наклона прямой равен
прямой, пересекающей ось ординат в точке t0. Тангенс угла наклона прямой равен 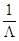 .
.
Если теплоемкость газа резко меняется с изменением температуры и степени превращения, то линия, изображающая процесс на диаграмме 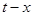 , будет искривлена и ее построение следует производить, пользуясь уравнением (4.15).
, будет искривлена и ее построение следует производить, пользуясь уравнением (4.15).
Для перенесения построенной на диаграмме 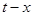 линии на диаграмму
линии на диаграмму 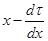 определяют значения степеней превращения при температурах изотерм диаграммы
определяют значения степеней превращения при температурах изотерм диаграммы 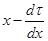 . Откладывают найденные значения на оси абсцисс диаграммы
. Откладывают найденные значения на оси абсцисс диаграммы 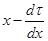 , восстанавливают перпендикуляры до пересечения с соответствующими изотермами и, соединяя полученные точки между собой, получают кривую, отображающую данный рабочий процесс. Искомое время контакта равно площади, ограниченной такой кривой, осью абсцисс и ординат x1 – x2.
, восстанавливают перпендикуляры до пересечения с соответствующими изотермами и, соединяя полученные точки между собой, получают кривую, отображающую данный рабочий процесс. Искомое время контакта равно площади, ограниченной такой кривой, осью абсцисс и ординат x1 – x2.
Пример 4.2. Рассчитать объем адиабатического реактора для дегидрирования изопропилбензола в a-метилстирол, если известны следующие данные: подача реакционной смеси при соотношении изопропилбензола к водяному пару 1:3 (массовое соотношение) равно 8 м3/с; степень превращения составляет 0,45; начальная температура дегидрирования равна 580 0С. Экспериментальные данные изображены на рисунках 4.3-4.4.
Решение. На рисунке 4.3 приведены изотермы для реакции дегидрирования изопропилбензола. На рисунке 4.4 представлена зависимость t от x для данного процесса.
|
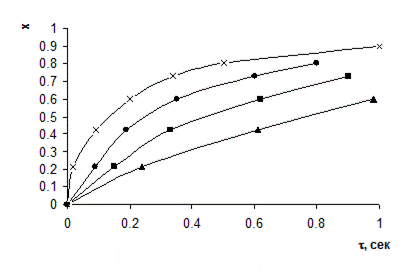
| Рис.4.3. Зависимость степени превращения x изопро- пилбензола от времени контакта t при различных темпе- ратурах t: x – 600 0C; · - 560 0C; ■ - 540 0C; ▲ - 520 0C |
Так как реакция сопровождается незначительным изменением объема, при расчетах пользуются диаграммой x-dt/dx. С помощью диаграммы x-t наносим на диаграмму x-dt/dx изотермы, соответствующие температурам 560, 540, 520 0С, находя dt/dx по тангенсу угла наклона касательных к изотермам в координатах x-t.
Построение на диаграмме x-dt/dx адиабаты, отвечающей заданной температуре начала реакции (580 0С), производим с помощью изотерм, нанесенных на эту диаграмму, и адиабаты, соответствующей начальной температуре 580 0С на диаграмме t-x.
По рисунку 4.4 находим, что температуре 560 0С соответствует степень превращения 0,19; 540 0С – степень превращения 0,38; 520 0С – степень превращения 0,56.
|
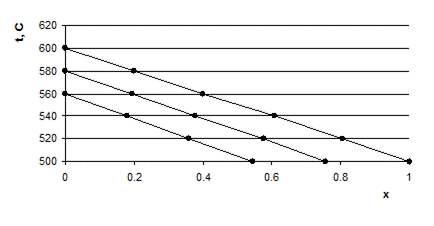
| Рис. 4.4. Зависимость температуры t от степени превращения x при адиабатическом дегидрировании изопропилбензола |
Затем на изотерме 560 0С (рис. 4.5) наносим точку, соответствующую x = 0,19; на изотерме 540 0С – точку, соответствующую x = 0,38; на изотерме 520 0С –точку, где x = 0,56.

Рис. 4.5. Диаграмма 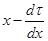 для процесса дегидрирования
для процесса дегидрирования
изопропилбензола.
________ изотермы при · - 560 0C; ■ - 540 0C; ▲ - 520 0C;
- - - - - адиабата
Соединив кривой эти точки, получаем адиабату, отвечающую начальной температуре реакции 580 0С. Находим время контакта как величину площади, ограниченной построенной адиабатой, осью абсцисс и ординатами, соответствующими значениям x, равным 0 и 0,45. Время контакта находится, как площадь криволинейной трапеции и равно 0,26 сек.
Отсюда объем реактора (рабочей части, заполненной катализатором)равен:
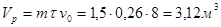 ,
,
где m =1,5 – принятый коэффициент запаса.
При теплообмене с теплоносителем, имеющим постоянную температуру
Чаще всего процесс контактирования проводят с отводом тепла (экзотермические реакции) или подводом тепла (эндотермические реакции), стремясь при этом приблизиться к оптимальному температурному режиму.
Для определения времени контакта также строят линию, отображающую данный процесс на диаграмме 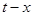 и затем переносят ее на диаграмму
и затем переносят ее на диаграмму 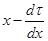 , как описано выше для адиабатического процесса. Необходимое время контакта также равно площади на диаграмме
, как описано выше для адиабатического процесса. Необходимое время контакта также равно площади на диаграмме 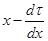 , ограниченной кривой, изображающей данный процесс, осью абсцисс и ординатами x1 и x2.
, ограниченной кривой, изображающей данный процесс, осью абсцисс и ординатами x1 и x2.
Если реакция сопровождается значительным изменением объема, то объем катализатора, необходимый для изменения степени превращения от x1 до x2, находится интегрированием
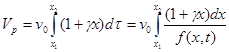 (4.17)
(4.17)
Расчет ведется совершенно так же, как и в случае постоянства объема. Только вместо диаграммы 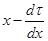 необходимо пользоваться аналогичной, специально построенной диаграммой
необходимо пользоваться аналогичной, специально построенной диаграммой 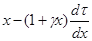 .
.
Дальнейшим развитием графоаналитического метода расчета реакторов Г.К.Борескова является метод, предложенный В.Б.Фальковским – для контактных аппаратов с внутренней теплообменной поверхностью, охлаждаемой или нагреваемой кипящим, конденсирующимся или движущимся по прямотоку или противотоку жидким или газообразным теплоносителем в случае сложных параллельных и последовательных обратимых и необратимых реакций.
При теплообмене с внешней средой, имеющей постоянную температуру, тепловой баланс можно выразить приближенным уравнением (4.3) или (4.4), справедливым, если тепло, используемое на изменение температуры реакционного газа, незначительно по сравнению с теплом, передаваемым через стенку, а температурный градиент в поперечном сечении контактного слоя невелик.
Умножая правую и левую часть уравнения (4.4) на 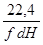
где f- площадь сечения слоя катализатора;
dH – высота элементарного участка катализаторного слоя, преобразуем его к виду
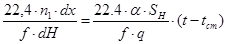 (4.18)
(4.18)
или
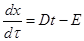 (4.19)
(4.19)
где 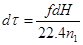 ;
; 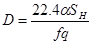
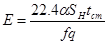
Уравнение (4.19) характеризуется прямой в координатах 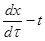 , причем отрезок на оси ординат равен свободному члену уравнения Е, а коэффициент D - тангенсу угла наклона этой прямой. При эндотермических реакциях, когда знак теплового эффекта реакции отрицателен, значение отрезка отсекаемого прямой на оси ординат является положительным, а угловой коэффициент D – отрицательным.
, причем отрезок на оси ординат равен свободному члену уравнения Е, а коэффициент D - тангенсу угла наклона этой прямой. При эндотермических реакциях, когда знак теплового эффекта реакции отрицателен, значение отрезка отсекаемого прямой на оси ординат является положительным, а угловой коэффициент D – отрицательным.
Точка пересечения прямой с кривыми равных степеней превращения дают искомую зависимость t = f(x) для данного случая теплообмена и позволяют построить график вспомогательной зависимости – обратной скорости реакции 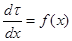 , известным графическим интегрированием которой находится время контакта, а следовательно и объем катализатора.
, известным графическим интегрированием которой находится время контакта, а следовательно и объем катализатора.
При теплообмене с прямоточнодвижущимся
теплоносителем, изменяющим свою температуру
В случае теплообмена реагирующего газа с прямоточнодвижущимся и изменяющим свою температуру теплоносителем, уравнение теплового баланса (4.20),(4.21)
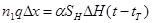 (4.20)
(4.20)
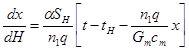
 (4.21)
(4.21)
преобразуется к виду
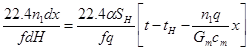 (4.22)
(4.22)
или 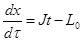
где 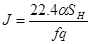
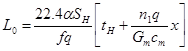 (4.23)
(4.23)
При противотоке реагентов и внешнего теплоносителя значение коэффициента L0 равно:
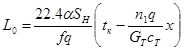 (4.24)
(4.24)
где 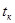 - конечная температура теплоносителя (0С), с которой он покидает реактор.
- конечная температура теплоносителя (0С), с которой он покидает реактор.
Расчет времени контакта и количества катализатора, производят аналогично ранее рассмотренному случаю.
Расчет реакторов вышеописанными способами с применением программных продуктов Microsoft Excel, MathCAD
Пример 4.3. Определить объем катализатора для дегидратации 2,18 кмоль/ч этанола на окиси алюминия до степени превращения 0,80 в трубчатом контактном аппарате с постоянной температурой стенки 420 0С и эффективностью теплообмена 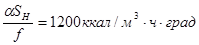 . Тепловой эффект реакции равен
. Тепловой эффект реакции равен
–9900 ккал/кмоль. Известны для данной реакции (на основании экспериментальных данных) изотермы (таб. 4.4) зависимости степени превращения от времени контакта при 250, 320, 415 0С.
Таблица 4.4
Зависимость конверсии от времени контакта при разных температурах проведения процесса
| Время, t×103сек | Конверсия, x | ||
| 250 0С | 320 0С | 415 0С | |
| 0.000 | 0.000 | 0.000 | |
| 0.595 | 0.459 | 0.358 | |
| 0.742 | 0.622 | 0.523 | |
| 0.808 | 0.705 | 0.618 | |
| 0.846 | 0.755 | 0.679 | |
| 0.870 | 0.789 | 0.721 | |
| 0.887 | 0.814 | 0.753 | |
| 0.900 | 0.832 | 0.777 | |
| 0.910 | 0.846 | 0.796 | |
| 0.917 | 0.857 | 0.812 |
Решение. 1. Рассчитаем коэффициенты линейного уравнения (4.19):
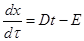 ,
,
где 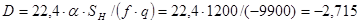
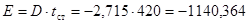
2. Строим в координатах dx/dτ - t рабочую линию.
Для этого составляем таблицу 4.5, в первой графе которой записываем любые значения температуры, а во второй находим значения скорости процесса, подставляя данные значения температур в уравнение (4.19), используя полученные коэффициенты D, E.
По значениям таблицы 4.5 строим рабочую линию (рис. 4.6).
Таблиц 4.5.
Координаты рабочей
линии адиабаты

| 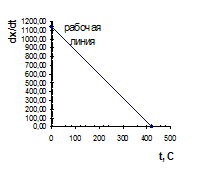 Рис. 4.6.
Рис. 4.6.
|
3. Рассчитываем скорость реакции в зависимости от времени при равных степенях превращения.
3.1. Строим графики зависимости конверсии от времени (рис. 4.7.) в координатах x-τ по данным таблицы 4.4.
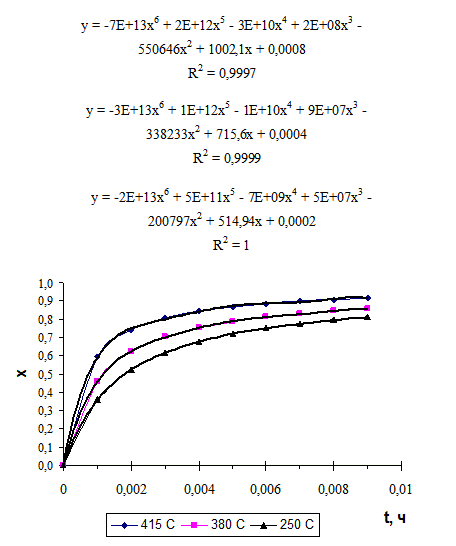
|
| Рис. 4.7. Изотермы дегидратации этанола на окиси алюминия |
3.2 Строим линию тренда для каждого графика и выводим на дисплей уравнения линии тренда и величину достоверности апроксимации.
Для упрощения дальнейших расчетов удобно использовать линию тренда с полиноминальной аппроксимацией 5 или 6 степени.
Полученные уравнения линии тренда описывают зависимость конверсии от времени при соответствующих температурах.
3.3 Для построения кривых равных степеней превращения в координатах dx/dτ - τ, рассчитываем значение времени при равных значениях конверсии.
Для этого составим таблицу 4.6. В первой строке соответствующего столбца значения конверсии пишем уравнение линии тренда описывающее процесс при данной температуре, подставляя вместо x значение τ из соседнего столбца. Первично присвоив τ любое числовое значение. Затем с помощью встроенной функции "ПОДБОР ПАРАМЕТРА" находим значения текущего времени для каждого значения равновесной конверсии при соответствующих температурах. Полученные значения времени необходимы для расчета значения скоростей реакции при равных степенях превращения.
| Таблица 4.6 Зависимость времени реакции при одинаковых значениях конверсии | |||||
| Конверсия при 415 0С | Время контакта τ,ч при 415 0С | Конверсия при 320 0С | Время контакта τ, ч при 320 0С | Конверсия при 250 0С | Время контакта τ,ч при 2500 С |
| 0,0 | 0,00000 | 0,0 | 0,00000 | 0,0 | 0,00000 |
| 0,10 | 0,00010 | 0,1 | 0,00015 | 0,1 | 0,00021 |
| 0,20 | 0,00022 | 0,2 | 0,00032 | 0,2 | 0,00046 |
| 0,30 | 0,00036 | 0,3 | 0,00054 | 0,3 |
Дата добавления: 2020-10-25; просмотров: 930;











