Расчет числа теоретических тарелок аналитическими методами

Аналитические методы определения числа теоретических тарелок. Здесь рассматривается метод Смокера для смесей, относительную летучесть которых можно считать постоянной, и метод Льюиса.

Метод Смокера [6]позволяет определить число теоретических тарелок отдельно для укрепляющей и исчерпывающей частей. Этот метод рекомендуется для тех случаев, когда линия равновесия близка к диагонали, что затрудняет применение графического метода. Для укрепляющей части число теоретических тарелок N_ук выражается уравнением:

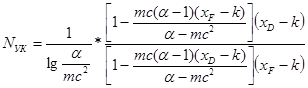, (5.21)

где a - относительная летучесть компонентов для укрепляющей части колонны; 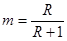- наклон рабочей линии укрепляющей части колонны; k - корень уравнения второй степени (0<k<1).

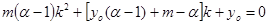(5.22)

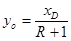- ордината точки пересечения рабочей линии укрепляющей части с осью ординат; с – параметр, определяемый по уравнению:

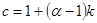(5.23)

Число теоретических тарелок для исчерпывающей части также определяют по уравнению (5.21), но вместо x_D и x_F берут x_F и x_W соответственно, используют относительную летучесть, угловой коэффициент m и начальную ординату у_о для исчерпывающей части колонны, а за k принимают отрицательный корень уравнения (5.22).

Дифференциальный метод Льюиса[6]рекомендуется в основном для насадочных колонн, так как в его основе лежит допущение о непрерывном изменении концентраций фаз. Число теоретических тарелок определяется следующими уравнениями:

для укрепляющей части колонны

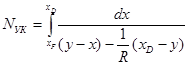(5.24)

для исчерпывающей части колонны

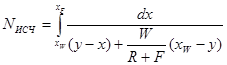(5.25)

Применять метод Льюиса для тарельчатых колонн и смесей с высокой относительной летучестью компонентов не рекомендуется.

Расчет многокомпонентных смесей методом «от тарелки к тарелке»заключается в определении числа теоретических тарелок путем последовательного определения равновесной и рабочей концентрации. Это наиболее точный метод расчета по сравнению с другими приведенными методами.

Если относительные летучести компонентов разделяемой смеси сильно отличаются друг от друга, желательно провести расчет для укрепляющей части, начиная его как с первой тарелки, так и с тарелки, на которую поступает исходная смесь, то есть во встречных направлениях. Общая последовательность расчета: 1-начинаем с кипятильника и продолжаем до тех пор, пока на какой-то тарелке полученный состав не будет соответствовать исходной смеси; затем продолжаем расчет, 2-начиная от верха колонны, до тех пор, пока на какой-то n-ой тарелке не будет находиться только оба ключевых компонента и следы других компонентов; после этого продолжаем расчет, 3-начиная от тарелки питания, пока не получим состав жидкости, идентичный составу на n-ой тарелке. На этом расчет заканчивается.

Для исчерпывающей части колонны:

равновесная концентрация

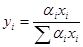(5.26)

рабочая концентрация

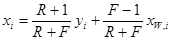(5.27)

Для укрепляющей части колонны:

равновесная концентрация

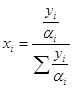(5.28)

рабочая концентрация

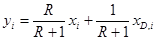(5.29)

Все изложенные выше методы применимы также для многокомпонентных смесей, если расчет вести по ключевым компонентам, т.е. смесь следует рассматривать как псевдобинарную.

7. Определение действительного числа тарелок.

Если известно число теоретических тарелок N_Т, то число действительных тарелок N_Д определяют из соотношения:

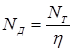(5.30)

где η – общий коэффициент полезного действия тарелок, или эффективность колонны.

Средний к.п.д. тарелки, выраженный в процентах, ориентировочно определяют по уравнению (5.31) (уравнение является весьма приближенным, так как не отражает влияния гидродинамических условий на эффективность тарелок).

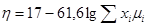(5.31)

где x_i – мольная доля i-го компонента в исходной смеси; μ_i – вязкость i-го компонента в жидкой фазе при средней температуре в колонне, спз.

8. Тепловой расчет колонны

Схема, иллюстрирующая тепловой расчет ректификационной колонны, представлена на рис. 5.5 [12]:

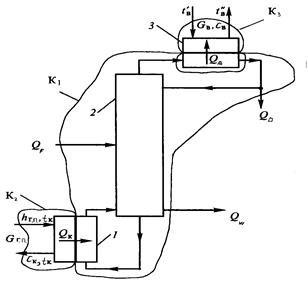
Рис.5.5. К тепловому расчету ректификационной колонны:

1-кипятильник, 2-колонны, 3- конденсатор

Согласно рисунку, уравнение теплового баланса можно записать в следующем виде (контур К₁):

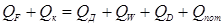, (5.32)

где Q_F – количество тепла, приходящее в колонну с сырьем, Вт, Q_к – количество недостающего тепла, приходящего в колонну из кипятильника, Вт; Q_Д – количество тепла, отводимого в дефлегматоре, Вт; Q_w – количество уходящего из колонны тепла с кубовым остатком, Вт; Q_D – количество уходящего тепла с дистиллятом, Вт; Q_пот – тепловые потери колонны в окружающую среду, Вт.

Расход теплоты в кубе – испарителе ректификационной колонны непрерывного действия определяют из уравнения теплового баланса колонны с дефлегматором – конденсатором:

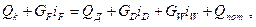(5.33)

где G_F, G_D, G_W – массовые расходы питания, дистиллята, кубового остатка, кг/с; i_F, i_D, i_W – соответствующие удельные энтальпии, Дж/кг.

Из уравнения (5.33) получаем:

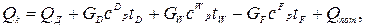(5.34)

где с^D_р, c^W_р, c^F_р – средние удельные теплоемкости, Дж/(кг*К); t_D, t_W, t_F – соответствующие температуры, К.

Расход теплоты, отдаваемой охлаждающей воде в дефлегматоре, рассчитывают в зависимости от условий процесса:

1. Если пары из верха колонны только конденсируются и покидают дефлегматор с той же температурой, то тепло рассчитывается по следующему уравнению:

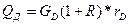(5.35)

где R – флегмовое число; r_D – удельная теплота конденсации паров в дефлегматоре, Дж/кг.

2. Если пары сконденсировавшись, выходят из конденсатора с более низкой температурой, то для расчета тепла, применяем уравнение (5.36):

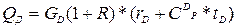, (5.36)

где С^D_Р – теплоемкость дистиллята с температурой выхода, Дж/(моль*К); t_D – соответствующая температура дистиллята, К.

Определив теплоты, подводимые и отводимые потоками (Q_к и Q_Д) находят расходы теплоносителей: G_к и G_Д. Расход греющего пара, подаваемого в кипятильник можно найти, составив тепловой баланс для контура К₂ (рис.5.5). Обозначим: h_г.п. – энтальпия греющего пара, t_к – его температура, К; С^к_р – теплоемкость конденсата. Тогда получим следующее уравнение:

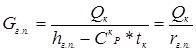, (5.37)

где r_г.п. – теплота конденсации греющего пара, Дж/кг.

Поверхность кипятильника F находим из основного уравнения теплопередачи:

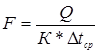, (5.38)

где К – коэффициент теплопередачи, Вт/(м²*К), Dt_ср – средний температурный напор, К.

Поток охлаждающей воды G_в с начальной температурой t^¢_в и конечной t^¢¢_в и теплоемкостью С^в_Р определяем из теплового баланса для контура К₃ (рис.5.5):

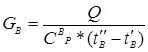(5.39)

Поверхность дефлегматора рассчитывается по уравнению (5.38).

9. Расчет основных размеров колонны

9.1 Объемный расход пара в колонне.Если производительность колонны по дистилляту равна D^¢ кг/кмоль, то объемный расход пара V_об (м³/сек) составляет:

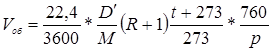(5.40)

где t – средняя температура в колонне, ^оС; R – флегмовое число; р – среднее давление в колонне, мм рт. ст.; М – средняя масса 1 кмоль дистиллята, кг/кмоль.

9.2 Определение диаметра тарельчатой ректификационной колонны производится по уравнению (5.41):

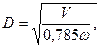(5.41)

где V – расход пара для наиболее нагруженного сечения, м³/с; 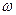– скорость пара, отнесенная к полному поперечному сечению колонны, м/с.

9.3 Рекомендуемую скорость пара в колонне рассчитывают по формуле:

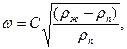(5.42)

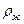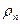где С – коэффициент, зависящий от конструкции тарелок, расстояния между тарелками, рабочего давления в колонне и нагрузки колонны по жидкости; и - плотности жидкости и пара, кг/м³.

Когда » ,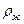

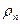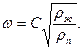(5.43)

На рис. 5.6 по данным, приведенным в [11], представлены в зависимости от расстояния между тарелками h значения коэффициента С для ректификационных колонн, работающих при атмосферном давлении и средних нагрузках по жидкости.

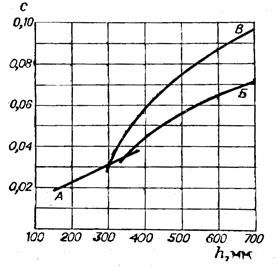
Рис. 5.6. Значение коэффициента С: А, Б – колпачковые тарелки с круглыми колпачками; В – ситчатые тарелки

После определения по уравнению (5.41) диаметра колонны его уточняют в соответствии с имеющимися нормалями.

На основании уравнений Клапейрона, плотность ρ любого газа при температуре Т и давлении плотность может быть рассчитана по формуле:

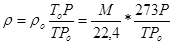, (5.44)

где ρ_о = М/22,4 кг/м³ – плотность газа при нормальных условиях (т. е. при Т_о=273,15 К и Р_о=760 мм рт. ст.=1,013*10⁵ Па) M – молекулярная масса газа, кг/кмоль; Т – температура, К.

Для определения плотности жидкости пользуются справочной литературой или рассчитывают методами прогнозирования [8].

Высоту тарельчатой ректификационной колонны (расстояния Н_Т) между верхней и нижней тарелками определяем по формуле (5.45) или из литературного источника [13]:

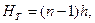(5.45)

где n – число тарелок в колонне; h – расстояние между тарелками.

Фиктивную скорость пара в точке захлебывания ω_з (если 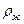» 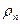) находят по уравнению (5.46), но с другим значением А. Для ректификационных колонн А = -0,125.

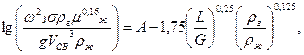(5.46)

где σ – удельная поверхность насадки, м²/м³;g – ускорение свободного падения, м/с²; V_СВ – свободный объем насадки, м³/м³; ρ_г и ρ_ж – плотности газа и жидкости, кг/м³; μ - динамический коэффициент вязкости жидкости, Па*с; L и G – массовые расходы жидкости и газа, кг/с; А = 0,022 для насадки из колец или спиралей [14], для ректификации А = -0,125.

Значения μ для жидкостей при различных температурах можно определить по номограмме, приведенной в литературе [5, стр. 556].

При отсутствии экспериментальных данных динамический коэффициент вязкости многих органических жидкостей (при 20 ^оС) приближенно может быть вычислен по следующей эмпирической формуле:

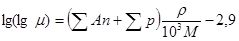, (5.47)

где μ – динамический коэффициент вязкости жидкости при атмосферном давлении и 20 ^оС, мП; ρ – плотность жидкости, кг/м³; М – молекулярная масса, кг/кмоль; А – число одноименных атомов в молекуле органического соединения; n – численное значение атомной константы; р – поправка на группировку атомов и характер связи между ними.

Атомные константы n и численные значения поправок р приведены в [5, табл. X].

Для определения μ по уравнению (5.47) удобна номограмма [5, стр. 553], на которой величина lg (lg μ) обозначена через у. Если у – величина положительная, следует пользоваться правой шкалой, при отрицательном значении у – левой. Каждому значению у соответствует значение μ – динамический коэффициент вязкости жидкости при 20 ^оС.

Для определения динамического коэффициента вязкости газов при различных температурах можно использовать номограмму, приведенную в следующем литературном источнике[5, рис. VI].

Динамический коэффициент вязкости газовых смесей может быть вычислен по приближенной формуле:

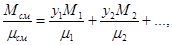(5.48)

где М_см, М₁, М₂,…, - молекулярные массы смеси газов и отдельных компонентов; μ_см, μ₁, μ₂, - соответствующие динамические коэффициенты вязкости; у₁, у₂, - объемные доли компонентов в смеси.

Изменение динамического коэффициента вязкости газов с температурой выражается формулой:

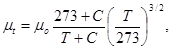(5.49)

где μ_о – динамический коэффициент вязкости при 0 ^оС; Т – температура, К; С – постоянная Сатерленда [5, табл. V].

Для смеси нормальных (неассоциированных) жидкостей значение μ_см может быть вычислено по уравнению:

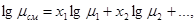(5.50)

где μ₁, μ₂…-динамические коэффициенты вязкости отдельных компонентов; х₁, х₂,…-мольные доли компонентов в смеси.

10. Гидравлический расчет тарелок сводится к расчету общего гидравлического сопротивления Dр, расчету минимальной скорости паров в отверстиях тарелки и расчету переливных устройств. Расчет для разных типов тарелок рассмотрен в следующей литературе [1, 2, 4, 5, 15, 16, 17].

11. Элементы механического расчета.

При выполнении механического расчета необходимо выполнить следующие пункты:

1. Вычислить толщину обечайки и крышек аппарата, исходя из условий прочности.

2. Провести механический расчет тарелок и их опорных устройств (балок).

3. Рассчитать опоры аппарата.

4. Рассчитать фланцевые соединения.

Подробный расчет разобран в следующих литературных источниках [18, 19].

Аналитический метод

Графический метод

Расчет к.п.д. тарелки и реального числа тарелок

Расчет числа теоретических тарелок

Рис. 5.7. Схема расчета ректификационных колонн

Примеры