Основные уравнения проектного теплового расчета
В первичные исходные данные для расчета теплообменного аппарата входят расходы теплоносителей, их начальные и конечные температуры. Недостающие величины определят из теплового баланса c учетом реальной температурной схемы процесса.
5.1.1 Уравнение теплового баланса.
В общем случае уравнение теплового баланса теплообменного аппарата имеет вид
| Q1=Q2+∆Q, | (5.1) |
где Q1 – количество теплоты, отдаваемое горячим теплоносителем в единицу времени, Вт;
Q2 – количество теплоты, воспринимаемое холодным теплоносителем в единицу времени, Вт;
∆Q – тепловые потери в окружающую среду, Вт.
Тепловые потери ∆Q зависят от режима работы теплообменного аппарата, его конструкции и качества тепловой изоляции. Величину тепловых потерь рассчитывают индивидуально для каждого теплообменника. При выполнении данного проекта принимаем потери равные 5 %.
Тогда уравнение теплового баланса принимает вид
| Q1∙0,95=Q2=Q, | (5.2) |
где Q – тепловая мощность теплообменного аппарата, Вт.
Тепловую мощность теплообменного аппарата для горячего теплоносителя рассчитывают по формуле
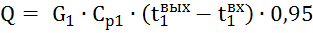 , ,
| (5.3) |
где G1- расход горячего теплоносителя, Дж/кг;
Ср1 – удельная теплоемкость горячего теплоносителя, Дж/(кг∙К);
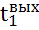 - температура выхода горячего теплоносителя, °C;
- температура выхода горячего теплоносителя, °C;
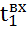 - температура входа горячего теплоносителя, °C.
- температура входа горячего теплоносителя, °C.
Тепловую мощность теплообменного аппарата для холодного теплоносителя рассчитывают по формуле
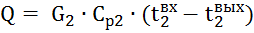 . .
| (5.4) |
Неизвестную температуру, с учетом (5.4), определяют по формуле
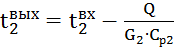 , ,
| (5.5) |
где 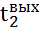 – температура выхода холодного теплоносителя, °C;
– температура выхода холодного теплоносителя, °C;
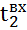 - температура входа холодного теплоносителя, °C;
- температура входа холодного теплоносителя, °C;
G2- расход холодного теплоносителя, Дж/кг;
Ср2 – удельная теплоемкость горячего теплоносителя, Дж/(кг∙К).
Если все температуры заданы, то находится расход одного из потоков.
Физико-химические свойства теплоносителей, необходимые для расчетов, такие как удельная теплоемкость, плотность, динамическая и кинематическая вязкость, удельная теплопроводность определяются с помощью специального программного обеспечения или по справочникам. При необходимости можно воспользоваться приложениями 2.А, 2.Б, 2.В, 2.Г, 2.Д, соответственно. При определении физико-химических свойств необходимо учитывать среднюю разность температур сырья в трубном и межтрубном пространстве
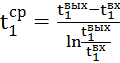 ; ;
| (5.6) |
Полученные результаты отображают на расчетной температурной схеме. Типовые температурные схемы теплообменных процессов отображены на рисунке 5.1.
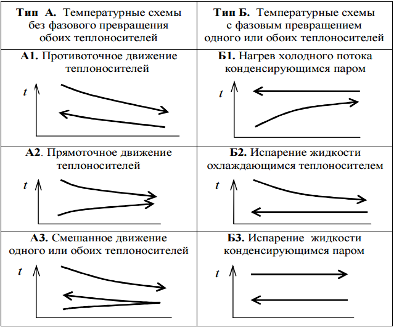
Рисунок 5.1 – Температурные схемы теплообменных процессов (на оси х откладывается температура, на оси y длинна) [6]
5.1.2 Уравнение теплопередачи.
Общая кинетическая зависимость для процессов теплопередачи, выражающая связь между тепловым потоком Q, поверхностью теплообмена F и температурным напором, представляет собой основное уравнение теплопередачи
Q = 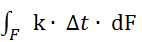 , ,
| (5.7) |
где k – коэффициент теплопередачи, Вт/(м2⋅К);
∆t - температурный напор, °C.
Коэффициент теплопередачи k и температурный напор ∆t в общем случае изменяются по поверхности теплообмена F. Для определения среднего коэффициента теплопередачи и усредненного по всей поверхности температурного напора ∆tср необходимо знать закон изменения k и ∆t по поверхности. В большинстве случаев коэффициент теплопередачи изменяется незначительно и его можно принять постоянным, изменение же ∆t будет зависеть от схемы включения теплообменника. Если считать величину k постоянной, а значение ∆t известным, то уравнение (5.7) примет вид
| Q = k∙F ∙∆tср, | (5.8) |
где ∆tср – средняя разница температур, °C.
Коэффициент теплопередачи k характеризует перенос тепла за счет теплопроводности и конвекции, он зависит от совокупности условий течения и теплообмена обеих сред в каналах теплообменного аппарата, от геометрической конфигурации поверхностей теплообмена, теплофизических свойств теплоносителей и материалов разделяющей их поверхности. В связи с этим, первоначально используем ориентировочный коэффициент теплопередачи из приложения 2 Е.
Средняя разность температур при прямотоке или противотоке теплоносителей равна
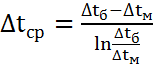 , ,
| (5.9) |
где Δtб и Δtм – разности температур (большая и меньшая) теплоносителей на концах теплообменника.
Если 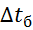 /
/ 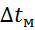 ≤2, то с достаточной точностью можно принимать
≤2, то с достаточной точностью можно принимать
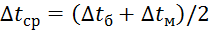 , ,
| (5.10) |
Расчет среднего температурного напора для многоходовых схем движения теплоносителей выполняют в два приема: определяют величину 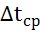 согласно (5.9) или (5.10), а затем вычисляют вспомогательные параметры:
согласно (5.9) или (5.10), а затем вычисляют вспомогательные параметры:
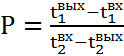 , ,
| (5.11) |
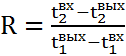 , ,
| (5.12) |
Тогда для многоходового теплообменного аппарата средняя разница температур будет вычисляться по формуле
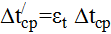 , ,
| (5.13) |
где 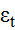 - поправочный коэффициент, вычисляемый с помощью рисунка 5.2.
- поправочный коэффициент, вычисляемый с помощью рисунка 5.2.
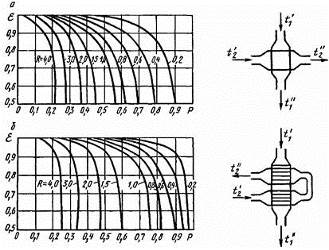
a – для теплообменников с перекрестно-смешанным током теплоносителей;
б – для теплообменников со смешанным током теплоносителей
Рисунок 5.2 – Поправочные коэффициенты 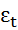 к расчету
к расчету 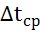 [6]
[6]
Таким образом, выбрав геометрию поверхностей теплообмена и принципиальную схему теплообменного аппарата в целом, после соответствующих расчетов k и ∆tср можно определить согласно (5.8) площадь теплопередающей поверхности, необходимой для обеспечения заданной тепловой мощности аппарата
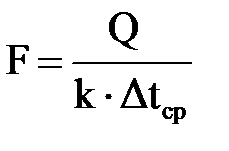
| (5.14) |
Дата добавления: 2020-10-25; просмотров: 649;











