Взаимное положение прямых
Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: а) быть параллельными; б) пересекаться; в) скрещиваться, т.е. не пересекаться, но и не быть параллельными. Рассмотрим на рис. 1.12 как при этом располагаются их проекции. Поскольку профильные проекции прямых можно построить по двум имеющимся, то на рис. 1.12 ограничимся двухкартинным комплексным чертежом.
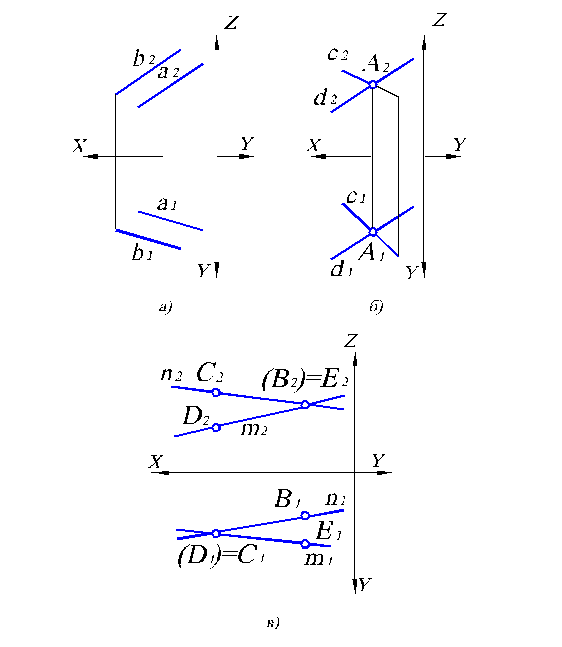
Рис. 1.12. Двухкартинный комплексный чертеж прямых, занимающих по отношению друг к другу следующее положение: а) а êêb; б) с Ç d; в) n ¸ m
В соответствии с одним из свойств ортогонального проецирования, если прямые параллельны, то их одноименные проекции параллельны (рис. 1.12, а). Если прямые пересекаются, то их проекции пересекаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А – точка пересечения прямых с и d). Если прямые скрещиваются, то их проекции пересекаются, но точки пересечения проекций не лежат на одной линии проекционной связи (на рис. 1.12, в см. точки С1 и В2) не лежат на одной линии проекционной связи. Тогда, следуя по вертикальной линии связи от точки С1, получим на каждой из прямых n2 и m2 соответственно две проекции: точки С2 и другой точки D2, а следовательно, на пересечении n1 и m1 лежат две точки С1 и D1, слившиеся в одну.
Точки, лежащие на одном проецирующем луче, называются конкурирующими. Такие точки могут быть только на скрещивающихся прямых, что очевидно из их пространственного положения. Точки, горизонтальные проекции которых совпадают, называются горизонтально–конкурирующими (на рис. 1.12, в см. точки C и D), а если совпадают фронтальные проекции, то точки называются фронтально-конкурирующими (на рис. 1.12, в точки В и Е).
При этом конкурирующие точки расположены на разном расстоянии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П2, будет закрыта от наблюдателя точкой, расположенной дальше от П2, а следовательно, ближе к наблюдателю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е – видимая, а точка В – невидимая. Аналогично С – видимая , а D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круглые скобки.
Дата добавления: 2016-07-27; просмотров: 2024;











