Плоскости частного и общего положения
Плоскостью частного положения называется плоскость, занимающая частное положение в пространстве, т.е. параллельная или перпендикулярная одной из плоскостей проекций.
Плоскости уровня
Плоскостью уровня называется плоскость, параллельная одной из плоскостей проекций, а следовательно, перпендикулярная двум другим. Тогда проекциями плоскости уровня будут прямые, параллельные соответствующим осям (рис. 2.2), вне зависимости от того, чем задана плоскость. От способа задания плоскости зависит лишь ее проекция на ту плоскость проекций, которой заданная плоскость параллельна.
Плоскость, параллельная П1, называется горизонтальной плоскостью уровня ( Г ). На рис. 2.2, а она задана тремя точками .
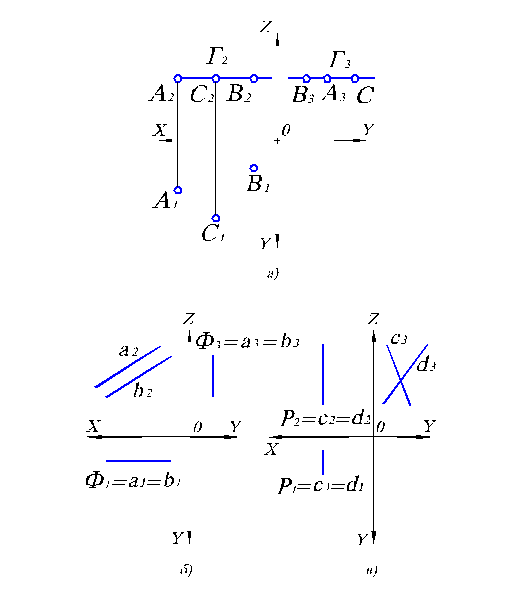
Рис. 2.2. Плоскости уровня на комплексном чертеже.
Плоскость, параллельная П2, называется фронтальной плоскостью уровня ( Ф ). Зададим ее параллельными прямыми (рис. 2.2, б). Причем, очевидно, расстояние от Ф1 до ОХ равно расстоянию от Ф3 до ОZ.
Плоскость, параллельная П3, называется профильной плоскостью уровня ( Р ). Считаем ее заданной пересекающимися прямыми (рис. 2.2, в).
Проецирующие плоскости
Проецирующей называется плоскость, перпендикулярная одной из плоскостей проекций. Исходя из определения, такая плоскость вырождается в прямую при проецировании на ту плоскость проекций, к которой она перпендикулярна.
Горизонтально-проецирующей называется плоскость, перпендикулярная П1, фронтально-проецирующей – перпендикулярная П2, и профильно-проецирующей – плоскость, перпендикулярная П3. На чертеже, первая из них задана плоской фигурой (рис. 2.3, а), вторая – точкой и прямой (рис. 2.3, б), третья - двумя параллельными прямыми (рис. 2.3, в).
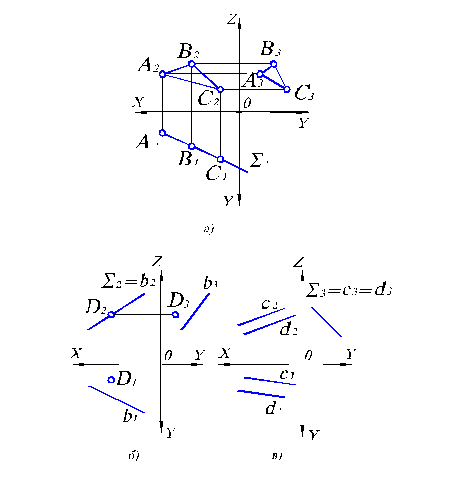
Рис. 2.3. Проецирующие плоскости на комплексном чертеже.
Плоскость общего положения
Плоскостью общего положения называется плоскость, не перпендикулярная и не параллельная ни одной из плоскостей проекций, а значит, расположенная под произвольным углом к каждой из них.
У такой плоскости все проекции будут невырожденные. Например, если плоскость общего положения задана плоской фигурой (треугольником), то все три проекции ее будут треугольниками (рис. 2.4).
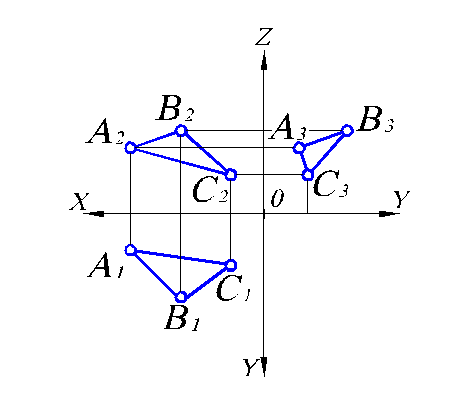

Дата добавления: 2016-07-27; просмотров: 2416;











