Определение реакций в кинематических парах механизма

Для определения реакций в кинематических парах надо предварительно разложить механизм на структурные группы. Каждая структурная группа вычерчивается отдельно в масштабе μ_l и к ее звеньям прикладываются соответствующие силы. Силовой расчет механизма начинают с определения давлений в кинематических парах структурной группы, наиболее удаленной от входного звена.

Определение реакций в кинематических парах рассмотрим на следующих примерах.

Кривошипно-шатунный механизм одноступенчатого компрессора (рис.6.2, а). В рассматриваемом примере имеется одна структурная группа, состоящая из звеньев 2–3 (рис.6.2, в).

Воздействие входного звена 1 и стойки 0 на звенья отсоединенной группы 2–3 заменяем силами реакций (см.рис.6.2, в). Одну из составляющих реакций вращательных кинематических пар удобно разложить по направлению звеньев, а вторую – перпендикулярно. Например, R₁₂ представим как сумму векторов двух составляющих

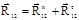. (6.7)

Первая цифра индекса показывает номер действующего звена, а вторая – номер звена, на которое производится действие. Например, R₁₂ – давление первого звена на второе, R₀₃ – действие стойки 0 на ползун 3.

В соответствии с принципом Даламбера условие равновесия структурной группы 2–3 имеет вид

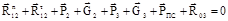. (6.8)

Это уравнение имеет три неизвестных: 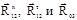. Реакцию следует определить из уравнения моментов сил, действующих на звено 2, составленного относительно шарнира С.

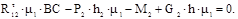(6.9)

Обратите внимание, если при решении уравнения (6.9) реакция 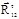будет иметь положительное значение, то её направление будет совпадать с направлением, указанным на чертеже (рис.6.2, в). Если реакция 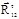будет иметь отрицательное значение, то на расчетной схеме направления вектора 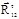следует изменить на противоположное.

Рис. 6.2. Силовой расчет кривошипно-шатунного механизма:

а – кинематическая схема механизма; б – план ускорений;

в – расчетная схема группы; г– план сил группы Ассура;

д – расчетная схема входного звена; е – план сил входного звена;

ж – рычаг Жуковского.

Величину векторов 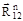и 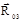определяем построением плана сил в масштабе μ_Р по уравнению (6.8) (рис. 6.2, г). Построение плана сил следует начинать с реакции 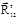и последовательно прикладывать все вектора сил, действующие на звено 2. К последнему вектору силы Р₂, действующему на звено 2, прикладываются вектора сил, действующие на звено 3. Через конец вектора последней силы Р_пс проводится линия действия реакции 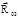, а через начало реакции 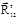– линия действия реакции 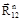. Линии действия реакци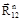и и 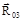проводятся до их взаимного пересечения. 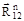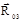Векторы сил и направляются так, чтобы многоугольник сил был замкнутым. При таком построении легко определить давление в промежуточном шарнире кинематической паре С по уравнению

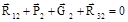. (6.10)

Модуль реакций R₁₂, R₀₃ и R₃₂ определяется из плана сил (рис. 6.2,г) по формулам

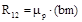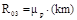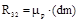; ; . (6.11)

Определив реакцию R₁₂, переходим к силовому расчету входного звена. Прикладывая к шарниру В (рис.6.2, д) реакцию 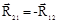, определяем уравновешивающую силу из уравнения моментов относительно шарнира А

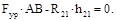(6.12)

Реакцию R₀₁ определяем из построения плана сил (рис.6.2, е) по уравнению

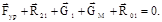(6.13)

Из плана сил находим .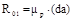

Точность определения уравновешивающей силы проверяем по теореме Н.Е. Жуковского о «жестком рычаге». Для этого вычерчиваем план скоростей механизма в исследуемом положении, повернутый на 90° (рис.6.2, ж), и в точках, одноименных точкам плана механизма, прикладываем соответствующие силы. Момент М₂ представляем в виде пары сил, приложенных в точках В и С перпендикулярно звену ВС так, что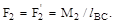

Направление векторов сил, приложенных к плану, должно совпадать с направлением этих векторов, приложенных к звеньям механизма.

Условие равновесия плана скоростей как рычага с точкой опоры в полюсе для нашего случая имеет вид

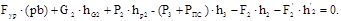(6.14)

Отсюда определяем F_ур. Значение F_ур, полученное по теореме Н.Е. Жуковского, сравниваем со значением этой силы, полученной в результате силового расчета.

Определение реакций в кинематических парах группы Ассура II класса 1-го вида (ВВВ). Рассмотрим данный вопрос на примере соломонабивателя зерноуборочного комбайна (рис.6.3).

Рис. 6.3. Силовой расчет группы типа ВВВ:

а – схема группы; б – план ускорений; в – план сил группы .

Пусть даны силы тяжести G₂ и G₃ звеньев 2 и 3; сила полезного сопротивления Р_пс; моменты инерции 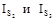относительно осей, проходящих через центры масс звеньев 2 и 3. Определим реакции в кинематических парах А, В, О₃ .

Вычисляем силы инерции (главные векторы Р_и и главные моменты сил инерции М_и) по формулам

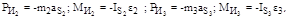(6.15)

где 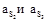– линейные ускорения центров масс звеньев 2 и 3, принимаем с планов ускорений (рис. 6.3, б);

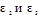– угловые ускорения звеньев 2 и 3.

Вычисленные силы инерции 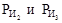прикладываем в точках S₂ и S₃ (рис.6.3, а) противоположно векторам 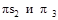(рис.6.3, б). Моменты от пар сил инерции М₂ и М₃ направляем противоположно угловым ускорениям .

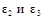Реакции во внешних парах А и О₃ разложим на две составляющие, направленные по осям звеньев 2 и 3 и перпендикулярно к этим осям, и

обозначим их соответственно через 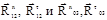. Тангенциальные составляющие находим из уравнений моментов всех сил относительно точки В для каждого звена в отдельности. Для звена 2 имеем:

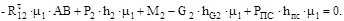(6.16)

Из этого уравнения находим 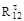. Аналогично составляем уравнение моментов для звена 3:

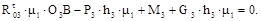(6.17)

Отсюда находим 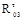. Все плечи в уравнения моментов подставляем в миллиметрах, взяв их непосредственно с чертежа.

Нормальные составляющие 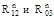определяем, решая графически векторное уравнение равновесия структурной группы (звенья 2,3),

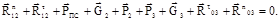(6.18)

В этом уравнении все силы, кроме 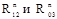, известны и по величине и по направлению. Реакции 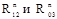известны только по направлению.

Уравнение (6.18) решаем графически, строя план сил в некотором масштабе 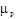(рис.6.3, в). Для этого последовательно откладываем все известные силы, перенося их из плана группы на план сил параллельно самим себе. Затем из начала вектора 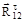и конца вектора 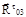проводим прямые, параллельные соответственно звеньям 2 и 3. Точка пересечения этих прямых определит длины векторов .

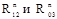Для определения реакций в шарнире В решаем графически векторное уравнение сил, приложенных к одному из звеньев, например, к звену 2. Отбрасываем звено 3 и его действие заменяем реакцией 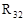, которую определяем из графического решения уравнения.

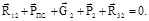(6.19)

Определение реакций в кинематических парах групп Ассура II класса 4-го вида. Этот вопрос рассмотрим на примере механизма строгального станка (рис.6.4). Данный механизм состоит из двух групп Ассура II класса 4-го вида (звенья 4–5) и 3-го вида (звенья 2–3).

Рассмотрим особенности силового расчета группы Ассура, состоящей из звеньев (4–5) (рис.6.4, г). Это группа образована двумя ползунами, соединенными между собой поступательной кинематической парой. На данную структурную группу действуют следующие силы: тяжести звена 5G₅, полезного сопротивления Р_ПС и инерции звена 5Р₅. Масса звена 4 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G₄ = 0 и Р₄ = 0.

Исполнительное звено (ползун 5) образуют со стойкой поступательную пару в точке Е^’ и дублирующую в точке Е^”.Реакции этих пар приводятся к равнодействующей R₀₅, приложенной в точке Е^”. В точке С свободной (внешней) парой является вращательная, соединяющая ползун 4 с кулисой 3. В общем случае реакция R₃₄ этой пары не известна по величине и направлению.

Направление реакции R₃₄ установим, рассмотрев равновесие звена 4 (рис.6.4, е). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R₃₄ и R₅₄. Значит, эти силы равны и противоположно направлены. R₅₄ – это сила действия направляющей звена 5 на звено 4. Известно, что без учета сил трения направление реакции R₅₄ перпендикулярно к направляющим ползуна 4, следовательно и реакция R₃₄ во вращательной кинематической паре будет иметь такое же направление.

Уравнение равновесия структурной группы 4–5 имеет вид

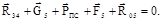(6.20)

В данном векторном уравнении неизвестными являются только две силы R₀₅ и R₃₄, поэтому его решение выполним графически методом построения плана сил (рис.6.4, д).

Определение реакций в кинематических парах групп Ассура II класса 3-го вида (рис.6.4, ж).Эта группа находится в равновесии под действием внешних сил: R₄₃ = –R₃₄, величина и направление которой

Рис. 6.4. Силовой расчет кривошипно-кулисного механизма:

а – кинематическая схема механизма; б – план скоростей;

в – план ускорений; г – расчетная схема группы 4–5;

д – план сил группы 4–5; е – расчетная схема ползуна 4;

ж – расчетная схема группы 2–3; з – план сил группы 2–3.

определены из предыдущих расчетов; силы тяжести G₃ звена 3; силы инерции и момента сил инерции звена 3, определение которых выполняются по зависимостям (6.21). Масса звена 2 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G₂ = 0, Р₂ = 0. Реакции, подлежащие определению: R₁₂, приложенная в центре шарнира А, и R₀₃, приложенная в центре шарнира О₃.

Вычисляем силы инерции, действующие на звено 3,

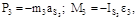(6.21)

где 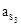– ускорение центра масс звена 3, берем с плана ускорений (рис.6.5, б), 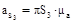(м/с²);

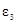– угловое ускорение звена 3.

Прикладываем вектор силы Р₃ в точку S₃ (рис.6.4,ж) противоположно вектору πS₃, а момент М₃ – к звену 3 противоположно вектору e₃ .

Составим уравнение равновесия всех сил, действующих на звенья 2,3,

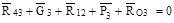. (6.22)

Это векторное уравнение можно решить графически, если предварительно найти модуль силы R₁₂. Направление реакции R₁₂ находим, рассмотрев равновесие звена 2 (рис.6.4 ). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R₁₂ и R₃₂ . Значит, эти силы равны и противоположно направлены. R₃₂ – это сила действия направляющей ВО₃ на звено 2. Известно, что без учета сил трения реакция R₃₂ направлена перпендикулярно к направлению ВО₃.

Зная направление R₁₂, найдем её модуль из уравнения моментов всех сил относительно точки О₃

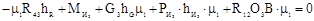, (6.23)

откуда находим R₁₂.

Уравнение (6.22) решаем графически методом построения плана сил. Реакция R₀₃ замыкает силовой многоугольник, построенный по уравнению (6.22).

Указания к силовому расчету механизмов с разветвленными кинематическими цепями (рис.6.5). Механизмы целого ряда двигателей и рабочих машин представляют собой не простые, а разветвленные кинематические цепи. Например, кривошипно-ползунные механизмы двухцилиндровых двигателей внутреннего сгорания. При силовом расчете этих механизмов нужно рассмотреть вначале группу Ассура, состоящую из звеньев 4–5, а затем – из звеньев 2–3 аналогично примеру (рис.6.2, а). В результате этих расчетов определяем реакции в кинематических парах А (2–1) и А (4–1) шатун – кривошип, т.е. R₂₁ и R₄₁. После этого производим силовой расчет ведущего звена.

Запишем уравнение сил, действующих на звено 1 (рис.6.5,б) механизма V-образного двигателя,

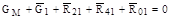, (6.24)

где G₁+G_М – вес кривошипа (коленчатого вала) с маховиком, P_и1= 0 так как а_s1 = 0.

Рис. 6.5. Расчетные схемы: а – простого кривошипа;

б, г – планы сил; в – разветвленного.

Векторное уравнение решаем построением плана сил (рис. 6.5,б), из которого находим величину и направление R₀₁ в кинематической паре О₁. Величину уравновешивающего момента М_ур, приложенного к звену 1, определяем из уравнения моментов сил, составленного относительно точки О₁.

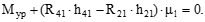(6.25)

Уравнение сил, действующих на звено 1 (рис. 6.5,в), механизма двухцилиндрового двигателя с вертикальным расположением цилиндров, имеет вид

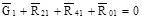. (6.26)

Из плана сил, построенного по уравнению (6.22) (рис. 6.5,г) определяем реакцию R₀₁ в паре кривошип 1 – стойка О. Величину уравновешивающего момента, приложенного к звену 1, определяем из уравнения моментов сил, составленного относительно точки О₁,

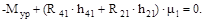(6.27)

Уравновешивающий момент может быть заменен уравновешивающей силой, приложенной в точке А кривошипа, при условии, что Р_ур = = М_ур /l_АВ .