Использование понятия полезности при определении размеров риска.

На принятие решения оказывают большое влияние субъективные качества лица, принимающего решение (ЛПР), такие как:

· финансовое состояние ЛПР;

· отношение ЛПР к риску вообще;

· настроение или состояние здоровья ЛПР;

· множество других, даже непосредственно не относящихся к бизнесу причин.

Теория полезности позволяет ЛПР влиять на денежный результат исходов согласно своим оценкам их полезности. Каждый может приспосабливать процесс принятия решения к своим запросам.

Пример 2.7.7. Для примера рассмотрим два варианта инвестиций 1000 руб.

По первому варианту без риска можно получить 10% прибыли на вложенный капитал, по второму варианту можно, либо потерять весь капитал с вероятностью 0.6, либо его удвоить с вероятностью 0.4.

В первом случае гарантированный выигрыш составит 100 руб., во втором случае средний выигрыш равен 0×0.6+1000×0.4=400 руб.

Относительно получаемого среднего выигрыша вторая альтернатива явно предпочтительна, и если игрок безразличен к риску, он ее и выберет. Если он к риску не безразличен, а подавляющее число людей именно таковыми и являются, то выбор будет зависеть главным образом от финансового состояния игрока. Игроки, имеющие скромный денежный доход, предпочтут не рисковать, и выберут гарантированный доход в 100 руб. Для игрока, обладающего достаточно крупным капиталом, проигрыш 1000 руб. невелик, и он предпочтет рискнуть. Рисковать будут также игроки, патологически склонные к финансовым авантюрам.

Таким образом, каждый игрок по-разному оценивает полезностьтого или иного исхода. Американскими учеными Дж. Нейманом и О. Моргенштерном была предложена методика численного определения функции полезности, и было показано, что игрок при принятии решения (выбор альтернативы) будет стремиться к максимизации ожидаемой полезности, которая вычисляется как математическое ожидание полезностей всех исходов, составляющих данную альтернативу.

Процедура построения индивидуальной функции полезности U(x) состоит из двух этапов.

Этап 1. Присваиваются произвольные значения полезностей выигрышам для худшего (х_min) и лучшего (x_max) исходов (например, U(x_min)=0 и U(x_max)=100). Тогда полезности промежуточных выигрышей будут находиться в интервале от 0 до 100.

Этап 2. Игроку предлагается на выбор: получить некоторую гарантированную сумму v, находящуюся между х_min и x_max, либо принять участие в игре, в которой с вероятностью р выигрывается сумма x_max и с вероятностью (1 – р) сумма х_min. При этом вероятность р меняется до тех пор, пока игрок станет безразличным в отношении к выбору между получением гарантированной суммы v и игрой. Пусть указанное значение вероятности равно р₀. Тогда

U(v)= р₀U(x_max)+ (1 – р₀)U(x_min).

Таким образом, строится функция полезности для любого v.

В общем случае график функции полезности может быть трех типов (рис. 2.7.1).

U U U

а б в

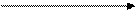
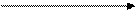
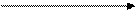
Рис. 2.7.1. Типы функций полезности Неймана – Моргенштерна для игрока, не склонного к риску (а), безразличного к риску (б), склонного к риску (в).

В рассмотренном выше примере x_min= –1000, а x_max =1000. Пусть U(x_min)=0 и U(x_max)=100. Необходимо оценить полезность гарантированного выигрыша v=100. Если игрок (средне обеспеченный) согласен принять участие в игре (выиграть 1000 с вероятностью р или проиграть 1000 с вероятностью (1 – р)) вместо гарантированного выигрыша в 100 руб. при условии, что р не менее 0.8, значит р₀=0.8 и U(100)=0.8×100+0.2×0 =80.

Ожидаемая полезность первой альтернативы будет равна 80, а ожидаемая полезность второй альтернативы 0.6×0+0.4×100=40, то есть для данного игрока предпочтительнее первая (безрисковая) альтернатива. В данном случае это решение прямо противоположно выбору, сделанному на основе критерия ожидаемого дохода, из-за учета риска, связанного с возможным исходом инвестиций по второму варианту.

Биматричные игры

В случае, когда интересы игроков различны, получаются две платежные матрицы: одна – матрица выплат игроку А, другая – матрица выплат игроку В. такие игры называются биматричными.

В общем случае биматричная игра – это игра с ненулевой суммой.