Основные типы экономических моделей
Математические модели, используемые в экономике, по ряду признаков, относящихся к особенностям моделируемого объекта, цели моделирования и используемого инструментария можно разделить на следующие классы:
Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финансовые показатели: ВВП, потребление, инвестиции, занятость, процентную ставку, количество денег и другие.
Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде. Вследствие разнообразия типов экономических элементов и форм их взаимодействия на рынке, микроэкономическое моделирование занимает основную часть экономико-математической теории. Наиболее серьезные теоретические результаты в микроэкономическом моделировании в последние годы получены в исследовании стратегического поведения фирм в условиях олигополии с использованием аппарата теории игр.
Теоретические модели позволяют изучать общие свойства экономики и ее характерных элементов дедукцией выводов из формальных предпосылок.
Прикладные модели дают возможность оценить параметры функционирования конкретного экономического объекта и сформулировать рекомендации для принятия практических решений. К прикладным относятся, прежде всего, эконометрические модели, оперирующие числовыми значениями экономических переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений.
Равновесные модели описывают такие состояния экономики, когда результирующая всех сил, стремящихся вывести ее из данного состояния, равна нулю, когда ни один из экономических субъектов не заинтересован в изменении состоянии объекта с помощью средств, которыми он располагает.
Равновесные модели занимают особое место в рыночной экономике. В нерыночной экономике неравновесие по одним параметрам (например, дефицит) компенсируется другими факторами (черный рынок, очереди и т.п.). Равновесные модели дескриптивны, описательны.
Статические модели описывают состояние экономического объекта в конкретный момент или период времени. В статических моделях обычно зафиксированы значения ряда величин, являющихся переменными в динамике, – например, капитальных ресурсов, цен и т.п.
Динамические модели включают взаимосвязи переменных во времени. Динамическая модель не сводится к простой сумме ряда статических, а описывает силы и взаимодействия в экономике, определяющие ход процессов в ней. Динамические модели обычно используют аппарат дифференциальных и разностных уравнений, вариационного исчисления.
Детерминированные модели предполагают жесткие функциональные связи между переменными модели.
Стохастические модели допускают наличие случайных воздействий на исследуемые показатели и используют инструментарий теории вероятностей и математической статистики для их описания.
Практический блок
Пример 1
Рассмотрим проблему математического моделирования на примере задачи оптимизации параметров реорганизационной политики.
Для большинства неплатежеспособных предприятий неудовлетворительная структура баланса отождествляется с отставанием фактического уровня текущей ликвидности от его норматива (Ктл<2) даже при достаточном уровне обеспеченности собственными средствами (Косс ³0,1).
Реорганизационные политики – процедуры реструктуризации балансов – позволяют перевести их в удовлетворительную структуру за счет реализации специально подобранного комплекса организационно-технических мероприятий. Но однозначно выбрать для практической реализации из возможных вариантов реорганизационных политик один, наиболее рациональный затруднительно, так как, если по прогнозируемым показателям платежеспособности, структуры баланса они равнозначны, то по прогнозным финансовым результатам могут быть противоречивыми.
Оценить предпочтительность каждого из этих вариантов оказывается возможным, если сформулировать задачу оптимизации реорганизационных политик с помощью математической модели, которая будет определяться текущим уровнем финансовой состоятельности, прежде всего, сложившимся уровнем платежеспособности.
Задача оптимизации основных параметров текущей деятельности может быть представлена следующей общей постановкой:
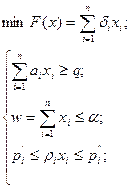
где F(x) – целевая функция задачи;
хi – независимые искомые переменные по направлениям реорганизационной политики (вектор управления структурой имущества: искомая величина продаж одного вида средств, приобретения другого, погашения долгов);
di – экспертная оценка приоритетности i-го направления реорганизации;
w – константа обеспечения текущей ликвидности (w=2КЗ – ОА; КЗ – краткосрочная задолженность, ОА – оборотные активы);
аi – коэффициенты при неизвестных переменных в ограничении на обеспеченность собственными оборотными средствами;
q – минимально-допустимый уровень обеспеченности собственными оборотными средствами (q = ВА + 0,1ОА – КР; ВА – внеоборотные активы, КР – капитал и резервы);
а – верхний предел допустимых продаж и приобретений активов;
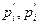 – соответственно нижняя и верхняя границы возможного изменения i-го вида активов;
– соответственно нижняя и верхняя границы возможного изменения i-го вида активов;
ri – удельный вес i-го вида активов предприятия в общей стоимости его имущества.
В частности, применительно к типичной неудовлетворительной структуре баланса Ктл < 2, Косс ³ 0,1, характерной для большинства неплатежеспособных предприятий, ищем такие х1 – объем продаж части активов, х2 – размер погашения кредиторской задолженности, чтобы выполнилось условие Ктл = 2 при сохранении Косс ³ 0,1. Тогда модель приобретает вид:
Ктл = (ОА + х1 – х2)/(КЗ – х2) = 2, откуда х1 + х2 = 2КЗ – ОА;
Косс = (КР – ВА + х1)/(ОА + х1 – х2) ³ 0,1, откуда
0,9 х1 + 0,1 х2 ³ ВА +0,1ОА – КР;
х2 – х1 £ a×ОА;
х1 £ b×ВА;
х2 £ g×КЗ,
где a, b, g – предельно допустимые для сохранения статуса деятельности предприятия размеры уменьшения соответственно оборотных активов (например, до 20%), внеоборотных активов (10%), краткосрочной задолженности (50%).
Целевая функция
min(d1х1 + d2х2),
где d1, d2 – экспертные оценки значимости продажи имущества и погашения наиболее срочных обязательств.
Приведенная выше задача может быть решена методами линейного программирования, которые будут рассмотрены в теме 2.2. Однако встречаются математические модели, которые решить аналитически невозможно. Для их решения существуют специальные методы численного решения. Особенностью таких методов является наличие погрешности в результатах. Погрешность в результатах определяется неточностью модели, т.е. ошибочностью или недостаточностью положений, лежащих в основе построенной модели, и погрешностью математических методов, с помощью которых проводился анализ изучаемой модели.
Представленные ниже в темах 2.2 – 2.9 модели и методы в основном ориентированны на те задачи, которые попадают в сферу исследования операций в управленческой и экономической деятельности и могут быть полностью или частично использованы при их математическом моделировании.
Пример 2. Из четырёх видов основных материалов (медь, цинк, свинец, никель) составляют три вида сплавов латуни: обычный, специальный и для художественных изделий. Цены единицы веса меди, цинка, свинца и никеля составляют 0,8 руб., 0,6 руб., 0,4 руб. и 1,0 руб., а единицы веса сплава, соответственно, 2 руб., 3 руб., 4 руб. Сплав для художественных изделий должен содержать не менее 6% никеля, не менее 50% меди и не более 30% свинца; специальный – не менее 4% никеля, не менее 70% меди, не менее 10% цинка и не более 20% свинца. В обычный сплав компоненты могут входить без ограничения. Производственная мощность предприятия позволяет выпускать (за определённый срок) не более 400 ед. веса обычного сплава, не более 700 ед. веса специального сплава и не более 100 ед. веса сплава для художественных изделий.
Построить математическую модель задачи нахождения производственного плана, обеспечивающего максимальную прибыль.
Решение. Обозначим через xij долю i-той компоненты (1-медь, 2- цинк, 3-свинец, 4-никель) в j-том виде сплава (1-обычный, 2-специальный и 3-для художественных изделий).
Тогда получим следующие ограничения модели:
x11 + x21 + x31 + x41 =1;
x12 + x22 + x32 + x42 =1; (2.1.1)
x13 + x23 + x33 + x43 =1.
Ограничения на количество компонент в смесях:
x12 ≥0.7; x22 ≥0.1; x32 ≤0,2; x42 ≥0,04;
x13 ≥0.5; x33 ≤0,3; x43 ≥0,06. (2.1.2)
Требование неотрицательности переменных:
xij ≥0. i=1,…,4, j=1,2,3. (2.1.3)
Целевая функция представляет собой сумму величин прибыли, получаемой с единицы веса каждого сплава:
2(0.8x11 + 0.6x21 + 0.4x31 + x41)+
3(0.8x12 + 0.6x22 + 0.4x32 + x42)+ (2.1.4)
4(0.8x13 + 0.6x23 + 0.4x33 + x43)→max
Ограничения (2.1.1-2.1.3) и целевая функция (2.1.4) представляют собой модель для получения искомой информации.
Тесты
1. Что является объектом и языком исследования в экономико-математическом моделировании:
а) различные типы производственного оборудования и методы его конструирования;
б) экономические процессы и специальные математические методы;
в) компьютерные программы и языки программирования.
2. Какое из утверждений верно:
а) экономико-математическая модель – это образ реального объекта в материальной или идеальной форме, отражающей существенные свойства моделируемого объекта и замещающий его в ходе исследования;
б) экономико-математическая модель – это математическое описание экономического процесса, произведенное в целях его исследования;
в) экономико-математическая модель – это математическое описание экономического процесса, необходимое для доказательства гипотез экономической теории.
3. В основе классификации экономико-математических моделей по содержательной проблеме лежит:
а) объект моделирования;
б) цель моделирования;
в) специальный программный комплекс.
4. Методологическое и методическое обоснование модели предполагает:
а) формализацию экономической проблемы;
б) изучение особенностей объекта моделирования и их отражение с помощью структуры разрабатываемой модели;
в) экспериментальные расчеты.
5. Что понимается под термином “исследование операций”?
а) применение математических методов для обоснования решений;
б) применение количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности, в том числе и в экономике;
в) применение математических методов для исследования бухгалтерских операций;
г) содержимое а и б пунктов;
д) содержимое а, б и в пунктов.
6. Когда впервые появился термин “исследование операций”?
а) в годы второй мировой войны;
б) в 50-ые годы;
в) в 60-ые годы;
г) в 70-ые годы;
д) в 90-ые годы.
7. Назовите примеры отраслей производственной сферы, в которых легко просматриваются характерные особенности задач исследования операций в экономике?
а) постройка участка магистрали;
б) продажа сезонных товаров;
в) снегозащита дорог;
г) выборочный контроль продукции;
д) все вышеназванное.
8. Какие решения называются оптимальными?
а) решения, по тем или иным признакам предпочтительные перед другими;
б) рациональные решения;
в) все согласованные решения;
г) все утвержденные решения;
д) все вышеназванные.
9. В чем заключается цель исследования операций?
а) предварительное количественное обоснование оптимальных решений;
б) указать одно-единственное строго оптимальное решение;
в) выделить область практически равноценных оптимальных решений, в пределах которой может быть сделан окончательный выбор;
г) содержимое пунктов а, б, в;
д) только содержимое пунктов а, б.
10. Что необходимо для того, чтобы сравнить между собой по эффективности разные решения?
а) нужно иметь какой-то количественный критерий, так называемый показатель эффективности;
б) нужно иметь целевую функцию;
в) показатель, отражающий целевую направленность операции;
г) содержимое пунктов а, б, в;
д) содержимое пунктов а, б.
Ответы к тестам
| 1) б | 6) г |
| 2) б | 7) б |
| 3) а | 8) а |
| 4) б | 9) г |
| 5) в | 10) г |
Контрольные вопросы
1. Привести классификацию экономических моделей.
2. Сущность и значимость экономико-математического моделирования.
3. Этапы экономико-математического моделирования.
4. Область применения экономико-математических моделей.
5. Экономическая значимость каждого этапа моделирования.
6. Сущность критерия практики.
7. Обязательные элементы математической модели.
8. Что такое оптимальное решение?
Дата добавления: 2020-10-25; просмотров: 1057;











