Вязкость агрегативно устойчивых дисперсных систем

В ряде случаев вязкость коллоидных систем практически не отличается от вязкости дисперсных систем. Ниже определенной скорости течения наблюдается ламинарное течение и подчинение законам Ньютона и Пуазейля.

Например, при ламинарном течении золей Au, Ag, Pt, As₂S₃, AgI и т.д. также справедливы законы Ньютона и Пуазейля. С другой стороны, часто наблюдаются большие отклонения от поведения нормальных жидкостей. Эйнштейном было показано, что введение в среду частиц дисперсной фазы приводит к увеличению вязкости системы. Он установил связь между вязкостью раствора и концентрацией дисперсной фазы для коллоидных систем.

Эту зависимость передает уравнение Эйнштейна:

h = h₀(1 + aj) или h_уд = 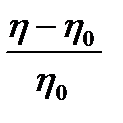= a×j, (4.11)

где a - коэффициент формы частиц (для сферических частиц a = 2.5, для удлиненных частиц a > 2,5); h_уд - удельная вязкость.

Следовательно, в отсутствие взаимодействия частиц среды с изометрическими частицами система ведет себя как ньютоновская жидкость, но с повышенной вязкостью.

Объемная концентрация рассчитывается по следующей формуле:

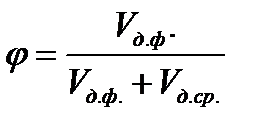(4.12)

η а б дисп.система

ньютон.ж

.

Р

Рис. 4.14. Зависимость вязкости от напряжения сдвига при ламинарном (а) и турбулентном (б) режимах течения для ньютоновских жидкостей и агрегативно устойчивых дисперсных систем.

Графическое представление уравнения (4.11) - прямая 1 на рис.4.14.

Рис.4.15. Зависимость вязкости систем от объёмной концентрации дисперсной фазы: 1 – линейная (уравнение Эйнштейна); 2 – для реальных систем с равноосными частицами; 3 – для систем с вытянутыми частицами дисперсной фазы.

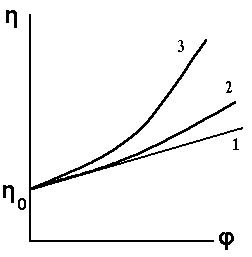
С увеличением концентрации дисперсной фазы возрастает взаимодействие между частицами, и обнаруживаются cильные отклонения от уравнения Эйнштейна. Вязкость концентрированных систем растет с увеличением j почти по экспоненте (линия 2 на рис.4.15), для них наблюдается зависимость вязкости от напряжения сдвига, т.е. закон Ньютона не выполняется. Эти отклонения от закона Ньютона и уравнения Эйнштейна обычно обусловлены взаимодействием частиц и образованием структуры, в которой частицы дисперсной фазы определенным образом ориентированы относительно друг друга (структурирование систем).

Зависимость вязкости таких систем от объёмной концентрации фазы даже при малых j не подчиняется уравнению Эйнштейна (кривая 3 на рис.4.15). Для описания зависимости h от j обычно используют уравнение:

h = h₀exp(a×j) или h = h₀(1 + aj + bj² +..) (4.13)

Условия применения уравнения Эйнштейна:

1) Сферические твердые частицы,

2) Разбавленная и устойчивая дисперсная система,

3) Пробег частиц мал по сравнению с пробегом системы,

4) Несжимаемая система,

5) Течение жидкости носит ламинарный характер,

6) Между частицами отсутствует скольжение.

Реальные дисперсные системы не подчиняются уравнению Эйнштейна по следующим причинам:

1) Наличие у частиц адсорбционных, сольватных слоев, а также ДЭС

2) Взаимодействие частиц дисперсной фазы,

3) Турбулезация потока,

4) Анизометричность частиц,

5) Временная флуктуация.