Молекулярно-кинетические свойства дисперсных систем

Броуновское движение

Тепловое движение частиц дисперсной фазы – факт общеизвестный. Английский ботаник Роберт Броун^(*) в 1827 г. под микроскопом наблюдал направленное движение очень малых частичек – спор папоротника, взвешенных в воде. Первые предположения о связи открытия Броуна с тепловым движением молекул были сделаны только в конце 19 в.

Броуновское движение проявляется в хаотическом непрерывном движении частиц дисперсной фазы под действием ударов молекул растворителя, находящихся в состоянии интенсивного молекулярно-теплового движения.

В зависимости от размера частиц траектория их движения может принимать различные формы.

х(путь)

t (время)

Рис.3.1. Траектория движения частицы дисперсной фазы

Количественная мера перемещения частиц – величина среднего смещения за время τ.

Теорию броуновского движения в 1905 – 1906 гг. создали независимо друг от друга А. Эйнштейн и М. Смолуховский^(**). При выводе уравнений они отказались от понятий «траектория» и «скорость» движения. В качестве основной характеристики движения ввели величину среднего сдвига (смещения) частицыDза время t. Это отрезок прямой, соединяющей начальную точку движения (при t = 0) с положением частицы в момент t в плоскости горизонтальной проекции, наблюдаемой в микроскоп. Путь частицы от одного положения частицы до другого при этом может быть каким угодно.

Смещением или сдвигом частицы называют расстояние между проекциями начальной и конечной точек траектории на ось смещений, но Δ может быть равной 0.

В связи с этим вычисляют среднюю квадратичную величину всех смещений без учета направления движения:

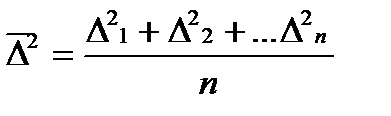(3.1)

Эта величина зависит лишь от свойств среды и размера частицы. Эту зависимость и получили Эйнштейн и Смолуховский:

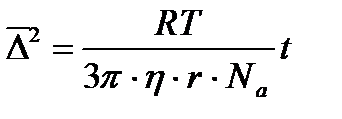, (3.2)

R- универсальная газовая постоянная, Т – абсолютная температура, h - вязкость среды, r – радиус частицы, N_a- число Авогадро.

Уравнение (3.2) получено Эйнштейном, уравнение Смолуховского отличается от него численным коэффициентом (64/27)². Уравнение Эйнштейна - Смолуховского позволяет измерить радиус частицы.

Дисперсным системам также присущи молекулярно – кинетические свойства. Более того, оказалось возможным их визуальное наблюдение – частицы дисперсной фазы участвуют в броуновском движении. А так как это движение можно было объяснить лишь движением молекул среды, то, по сути, это было первое прямое доказательство существования молекул (ещё в начале XX века в некоторых учебниках химии можно было прочитать следующее определение: «молекулы – это воображаемые частицы, из которых состоят тела»).

Удалось вывести основные законы, общие для молекул и коллоидных частиц. Экспериментальное их подтверждение явилось на рубеже XIX—XX вв. триумфом молекулярно-кинетической теории, завоевавшей всеобщее признание.