Седиментация суспензий
В свободнодисперсных системах частицы дисперсной фазы могут перемещаться по всему объему системы. Частицы грубодисперсных систем (суспензий, эмульсий и др.) не участвуют в броуновском движении и в зависимости от соотношения плотностей частиц и среды либо осаждаются под действием силы тяжести, либо всплывают под действием силы Архимеда.
Процесс оседания частиц дисперсной фазы в жидкой или газообразной среде под действием силы тяжести называют седиментацией, а процесс всплытия - обратной седиментацией.
На частицы, находящиеся в жидкости действуют две силы
- сила тяжести F=mg
и выталкивающая сила - сила Архимеда(*) Fa.
Равнодействующая этих сил - сила, вызывающая седиментацию Fc. Она равна:
Fc = mg - Fa = V×r×g - V×ro×g = V×g×(r - ro), (3.7)
где V - объем частицы, g - ускорение силы тяжести, r и ro- плотности частиц и среды, соответственно.
Под действием Fc частицы начинают двигаться с ускорением, но по мере роста скорости увеличивается и сила сопротивления среды, пропорциональная скорости движения Fтр = B×U. Наконец, наступает момент, когда Fc становится равной Fтр и частица начинает двигаться равномерно с постоянной скоростью U:
V×g×(r - ro) = B×U и U = V×g×(r - ro)/B (3.8)
Здесь B - коэффициент трения среды. Для сферических частиц, движущихся ламинарно в жидкости, коэффициент B обычно выражают законом Стокса(*):
B = 6×p×h×r (3.9)
Тогда скорость равномерного движения равна:
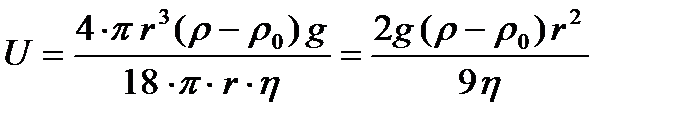 (3.10)
(3.10)
или
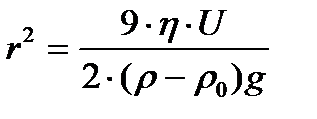 = K×U, (3.11)
= K×U, (3.11)
где h - вязкость жидкости, r - радиус частицы.
Скорость осаждения частиц можно рассчитать, зная путь частицы при осаждении H и время её осаждения t: U = H/t. Окончательно выражение для радиуса частиц имеет вид:
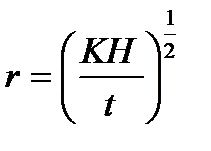 (3.12)
(3.12)
Это уравнение лежит в основе седиментационного анализа дисперсности грубодисперсных коллоидных систем, целью которого является установление минимального, максимального и наивероятнейшего радиусов частиц системы, а так же - распределения частиц по радиусам.
По такому закону происходит осаждение частиц в суспензиях, аэрозолях, эмульсиях.
Условия соблюдения законов седиментации
(зaкона Стокса)
1. Независимость осаждения частиц (разбавленные системы, иначе тормозится движение частиц из-за их столкновения).
2. Ламинарность движения
3. Дисперсность частиц от 0,1 мкм до 100 мкм, так как частицы с диаметром меньше 0,1 мкм обладают заметным броуновским движением, а частицы с диаметром, большим 100 мкм, движутся равноускоренно (возникает турбулентность).
4. Сферическая форма частиц. Частицы неправильной формы ориентируются в направлении движения. Для применения закона Стокса используют в этом случае понятие эквивалентного радиуса (т.е. радиуса сферы частиц, оседающих с той же скоростью, что и реальные частицы).
Способность к седиментации принято выражать через константу седиментации, которая определяется скоростью осаждения:
Sсед= V(ρ-ρo)/gВ= U/g (3.13)
Для сферических частиц Sсед=2 r2 (ρ-ρo)/9η, единица измерения – Сведберг(*): 1Сб=10-13 с.
Для аэрозолей, суспензий, эмульсий константа седиментации очень велика, поэтому используют мегаСведберги (МСб) или с. Для частиц кварца (радиус 10-3 см) Sсед = 3,25 10–5 с= 325 МСб=0,325 ГСб.
Таблица 3.1
Скорость седиментации сферических частиц SiO2 в H2O
| r частицы, мкм | 0,1 | 0,01 | 0,001 | ||
| Uсед, см/с | 3,6 10-2 | 3,610-4 | 3,610-6 | 3,610-8 | 3,610-10 |
| Время оседания на 1см | 28с | 46,5 мин | 77,5 ч | 323 дня | 89 лет |
Дата добавления: 2016-07-27; просмотров: 3130;











