Общий порядок оценки
Три величины, необходимые для оценки генерального параметра, – выборочный показатель ( 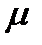 ), критерий надежности (t) и показатель точности (
), критерий надежности (t) и показатель точности ( 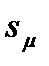 ) – определяются следующим образом.
) – определяются следующим образом.
Выборочный показатель ( 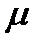 ) рассчитывается по выборочным материалам способом, изложенным при описании этого показателя.
) рассчитывается по выборочным материалам способом, изложенным при описании этого показателя.
Критерий надежности (t) определяется заранее, при планировании исследования, исходя из представления о большей или меньшей ответственности возможных результатов работы. Критерий надежности – это показатель вероятности безошибочных прогнозов.
Практика биологических работ выработала три основных порога вероятности безошибочных прогнозов: при обычной ответственности
b1 = 0,95, при повышенной ответственности b2 = 0,99 и при высокой ответственности b3 = 0,999.
Критерий надежности (t) связан с этими тремя порогами вероятности безошибочных прогнозов (b) при достаточно больших выборках так, как это показано в таблице 10.1.
Таблица 10.1 – Три порога надежности (вероятности безошибочных прогнозов)
| Порог | Применение | Вероятность безошибочных прогнозов | Критерий надежности | Объем выборок |
| Обычные требования надежности | β1 = 0,95 | t1= 1,960 | n1 > 30 | |
| Повышенные требования | β2 =0,99 | t2=2,576 | n2 > 100 | |
| Высокие требования надежности | β3 = 0,999 | t3 = 3,291 | n3 > 200 |
Для выборок, объем которых меньше указанного в таблице 10.1, и вообще для выборок любого объема значение t определяется по таблице критериев Стьюдента, в которых критерии надежности приводятся для любого объема выборок в зависимости от числа степеней свободы данного показателя, для каждого из трех порогов вероятности безошибочных прогнозов. Таблицы критериев Стьюдента приведены в учебниках по математической статистике.
При отсутствии таблицы критериев Стьюдента стандартные значения критерия надежности можно определить с достаточным приближением по формуле:
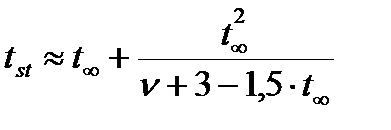 ; (10.1)
; (10.1)
tst – стандартное значение критерия при числе степеней свободы n;
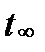 – критерий надежности для достаточно больших выборок
– критерий надежности для достаточно больших выборок
(t1 = 2.0; t2 = 2,6; t3 = 3,3);
Для обычных требований надежности (b = 0.95) эта формула приобретает более простой вид:
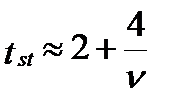 ; (10.2)
; (10.2)
Показатель точности или ошибка репрезентативности выборочного показателя определяется на основе выборочных данных по формулам математической статистики.
Ошибка средней арифметической:
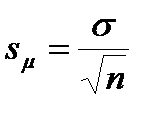 ; (10.3)
; (10.3)
Ошибка среднего квадратического отклонения:
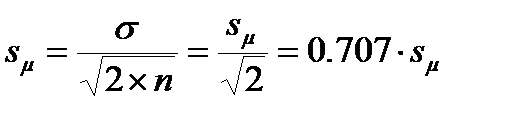 ; (10.4)
; (10.4)
Ошибка коэффициента вариации:
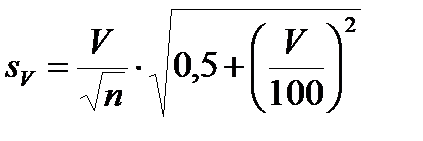 ; (10.5)
; (10.5)
Ошибка разности средних:
а) при некоррелированных выборках:
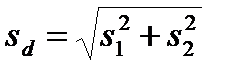 ; (10.6)
; (10.6)
б) при коррелированных выборках:
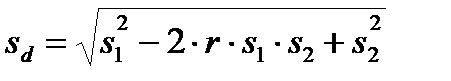 ; (10.7)
; (10.7)
(r – коэффициент корреляции)
Ошибка показателя асимметрии:
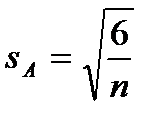 ; (10.8)
; (10.8)
Ошибка показателя эксцесса:
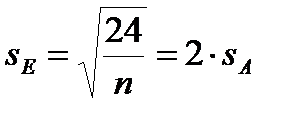 ; (10.9)
; (10.9)
Средняя ошибка суммы нескольких средних:
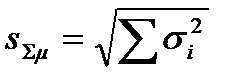 ; (10.10)
; (10.10)
Средняя ошибка произведения двух выборочных средних:
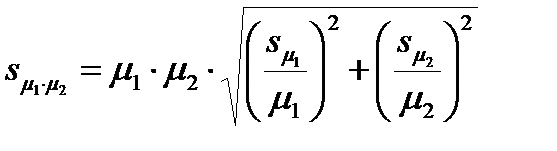 ; (10.11)
; (10.11)
Средняя ошибка частного двух выборочных средних:
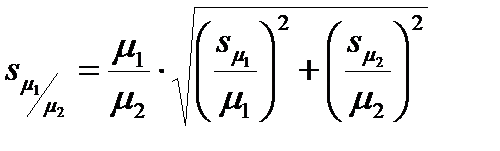 ; (10.12)
; (10.12)
Средняя ошибка разности выборочных средних двух независимых распределений.
При n1 = n2:
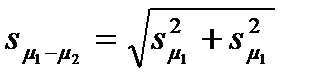 ; (10.13)
; (10.13)
При n1 ≠ n2:
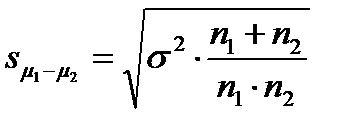 ; (10.14)
; (10.14)
Объединенная дисперсия двух выборок:
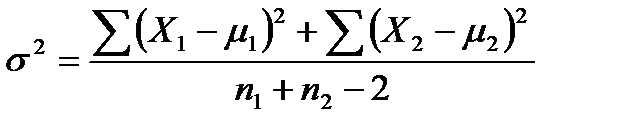 ; (10.15)
; (10.15)
Средняя ошибка разности в парных опытах:
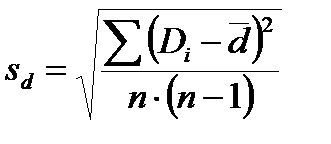 ; (10.16)
; (10.16)
Di – разности между вариантами сопряженных рядов X1 и X2;
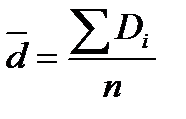 ; (10.17)
; (10.17)
n – общее число парных наблюдений.
Итак, для того чтобы оценить генеральный параметр для количественных признаков в форме доверительных границ необходимо:
1 Проверить на нормальность распределения исходных данных.
2 Установить число степеней свободы по правилам, приведенным при описании оценки каждого параметра.
3 Установить, исходя из ответственности исследования (таблица 10.1), порог вероятности безошибочных прогнозов
(β1 = 0,95, β2= 0,99, β3= 0,999).
4 В соответствии с числом степеней свободы найти значение критерия надежности t по таблице стандартных значений критерия Стьюдента. При отсутствии таблицы показатель надежности для данного исследования можно приближенно определить по приведенным формулам. Если объем выборки превышает нижние пределы больших выборок (n > 30, n > 100, n > 200), то показатели надежности берутся постоянные для каждого порога вероятности:
t1 = 2.0; t2 = 2.6; t3 = 3,3.
5 Рассчитать ошибку выборочного показателя по формулам, приведенным выше и указанным при описании оценки каждого параметра.
6 Определить возможную погрешность оценки генерального параметра, помножив критерий надежности на ошибку репрезентативности 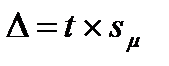 .
.
7 Установить доверительные границы генерального параметра; возможный максимум: 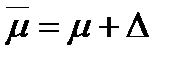 и гарантированный минимум:
и гарантированный минимум: 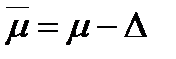 .
.
Дата добавления: 2020-10-25; просмотров: 804;











