Применение логического вывода для анализа схем.

Язык Пролог имеет множество применений. Рассмотрим в качестве простого примера его применения анализ логических схем [C87]. На рис. 2.4 представлена логическая схема полусумматора - основного блока двоичных сумматоров.

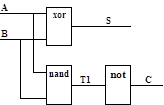
Рис. 2.4. Схема полусумматора

Описание этой схемы на Прологе может быть представлено следующим образом:

half_add(A,B,S,C) Ü xor(A,B,S), nand(A,B,T1), not(T1,C).

Необходима спецификация каждой элементарной функции (базовой подсхемы), включенной в это описание. Такая спецификация прямо повторяет соответствующие таблицы истинности:

xor(0,0,0).

xor(0,1,1).

xor(1,0,1).

xor(1,1,0).

nand(0,0,1).

nand(0,1,1).

nand(1,0,1).

nand(1,1,0).

not(0,1).

not(1,0).

Целями Пролога для этой программы могут быть, например, следующие:

? half_add(0,0,S,C).

(Каковы выходы S и C этой схемы при входах 0,0? Ответ - S=0, C=0.)

? half_add(A,B,0,1).

(При каких входах выход S будет единичным, а выход C - нулевым? Ответы - А=0, В=1; А=1, В=0.)

? half_add(А,В,Х,Х).

(При каких входах схемы выходы S и С будут совпадать? Ответ - А=0, В=0, Х=0.)

? half_add(X,X,X,1).

(Может ли быть у схемы выход С равным 1 при одинаковых значениях ее входов и выхода S? Ответ - no.)

Приведенный пример показывает огромное разнообразие возможностей анализа логических схем с помощью Пролога.

Экспертные системы

Возможности логического программирования на основе статического описания ситуации (состояния некоторой прикладной области реального мира) выполнять логический вывод с получением нового знания в настоящее время все шире используется в разнообразных системах поддержки принятия решений в сложных ситуациях. Мы рассмотрим упрощенное описания одной из реально используемых на практике систем управления в компьютерных сетях и вычислительных системах Flipper, разработка которой недавно была завершена в Европейской исследовательской лаборатории фирмы Хьюлетт-Паккард [PGM93]. Flipper позволяет описать сложную вычислительную систему, как аппаратные, так и программные ее компоненты, таким образом, чтобы обеспечить решение задач ее управления в процессе ее функционирования. Flipper выполняет свои функции управления на основе представления модели управляемой системы в виде логических правил, подобных записи правил в языке Пролог.

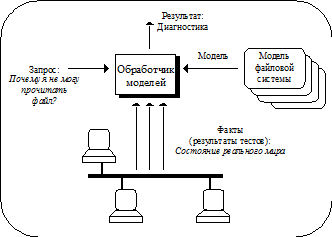
Модели, задающие правила функционирования вычислительной системы, используют синтаксис, близкий записи правил языка Пролог. Например, правило, определяющее права доступа пользователя к файлу, имеет вид:

[User user] has [String mode] acсessTo [File file]

IF

[user] isSuperUser;

|

[user] isOwnerOf [file],

[file] ownerMode [mode];

|

~ [user] isOwnerOf [file],

[file] isInGroupOf [user],

[file] groupMode [mode];

|

~[user] isOwnerOf [file],

~[file] isInGroupOf [user],

[file] worldMode [mode]

Очевиден смысл этих правил: любой объект user класса User имеет право доступа mode класса String к объекту file класса File, ЕСЛИ этот объект user является привилегированным (SuperUser), ИЛИ если этот объект user является владельцем этого объекта file И тип доступа владельца к этому файлу совпадает с типом mode, ИЛИ … . Фактически, весь фрагмент - это описание правила принадлежности троек объектов <пользователь, файл, тип_доступа> к некоторому отношению "Пользователь_Имеет_к_файлу_Право_доступа".

Проверка запроса о том, почему некоторый конкретный пользователь не имеет доступа к конкретному файлу с конкретным правом доступа, состоит в логическом выводе правильности запроса

? [петров] has [update] accessTo [compiler.exe]

после того, как экспертная система затребует из реального мира конкретные сведения по подлежащим проверке отношениям "Быть привилегированным пользователем", "Быть владельцем файла" и т.д.

Задачи к главе 2.

2.1 Какие перечисленные ниже логические формулы являются следствиями других формул?
(а) ху; (б) х ÞØу; (в) Øху; (г) хÅØу; (д) ØхÞу; (е) х¯у; (ж) Ø(ху); (з) хÚу; (и) true; (к)false.

2.2 Доказать, что перечисленные в п.2.3 силлогизмы описывают правильные схемы рассуждений.

2.3 Пусть установлено, что если сеть Петри инвариантна, то она ограничена. Что можно сказать о неинвариантной сети Петри? Что можно сказать о неограниченной сети Петри?

2.4 Известно, что если число делится на 6, оно делится на 3 и на 2. Сформулировать контрапозицию.

2.5 Пусть справедлива теорема: “Нильпотентный идеал является модулярным и радикальным”. Нуждаются ли в доказательствах следующие утверждения: “Если идеал не нильпотентный, то он не радикальный” и “Если идеал не модулярен, то он не нильпотентный”

2.6 Пусть справедлива теорема: “Для того, чтобы сеть Петри была ограничена и жива, достаточно, чтобы она была согласована и инвариантна”. Известно, что некоторая сеть Петри не ограничена. Что еще можно сказать о ней? Что можно сказать о неинвариантной сети Петри?

2.7 Предположим, что справедлива теорема: “Сеть Петри согласована и инвариантна только если она жива и ограничена”. Как доказывать эту теорему? Определить, какие из следующих утверждений являются следствиями этой теоремы::
(а) Сеть Петри ограничена только в случае, если она инвариантна;
(б) Несогласованность сети Петри является достаточным условием отсутствия у нее живости и ограниченности;
(в) Если сеть Петри не согласована, то она не может быть неживой, но ограниченной.

2.8 На какие этапы должно быть разбито доказательство утверждения: “Для того, чтобы МП-автомат был детерминированным и ограниченным, достаточно, чтобы распознаваемый им язык относился к классу LR(k) или к классу LL(k)”.

2.9 [П68] Справедливы ли утверждения:
а) Если верно, что дифференцируемая функция непрерывна, то невозможно, чтобы функция была дифференцируема и разрывна;
б) Если верно, что невырожденная матрица имеет обратную, то также справедливо, что матрица либо вырождена, либо имеет обратную.

2.10 Пусть известно, что хроничные сепульки латентны или бифуркальны. Какие из следующих утверждений в этом случае истинны:
а) сепульки не хроничны только в случае отсутствия у них свойства латентности;
б) латентность сепулек не является необходимым условием их хроничности или бифуркальности;
в) сепульки бифуркальны только в случае их хроничности либо латентности;
г) хроничность сепулек является достаточным условием их латентности или бифуркальности;
д) для того, чтобы сепульки были бифуркальны достаточно только, чтобы они были хроничны;
е) для нехроничности сепулек необходимо отсутствие у них как бифуркальности, так и латентности.

2.11 [C85] Мистер МакГрегор, владелец лавки из Лондона, сообщил в Скотланд-Ярд, что его ограбили. По обвинению владельца лавки были арестованы три подозрительных личности А, В и С. На основании его показаний, данных под присягой, было установлено, что:

(а) Каждый из подозреваемых А, В и С в день ограбления был в лавке и никто туда больше не заходил;

Следующие факты были неоповержимо установлены следствием:

(б) Если А виновен, то у него был ровно один сообщник;
(в) Если В невиновен, то С тоже невиновен;
(г) Если виновны ровно двое подозреваемых, то А - один из них;
(д) Если С не виновен, то В тоже не виновен.

Против кого Скотланд-Ярд выдвинул обвинение?

2.12 Трое рецидивистов, А, В и С, подозреваются в преступлении. Неопровержимо установлены следующие факты:
(1) Если А виновен, а В невиновен, то в деле участвовал С;
(2) С никогда не действует в одиночку;
(3) А никогда не ходит на дело вместе с С;
(4) Никто, кроме А, В и С в преступлении не замешан, но по крайней мере один из этой тройки виновен.
Можно ли на основании этих фактов выдвинуть обвинение против В? Против В или С? Против А?

2.13 [C85] В примере 2.6 инспектор Крейг поговорил с третьим обитателем больницы, Адамсом. На вопрос: “Кто Вы?” Адамс ответил нечто такое, что дало Крейгу основание считать, что Адамс - сошедший с ума доктор. Что сказал Адамс?

2.14 [Ш88]. По обвинению в ограблении перед судом предстали А, В, С и D. Установлено следующее:
(1) если А и В оба виновны, то С был их соучастником;
(2) Если А виновен, то по крайней мере один из двух, В и С, был его соучастником;
(3) С всегда “ходит на дело” вместе с D;
(4) Если А не участвовал в ограблении, то там был D.
Какие выводы можно сделать отсюда? Можно ли отсюда заключить, что В виновен? Можно ли заключить, что виновны А либо D?

2.15 [ЧЛ83]. Проблема химического синтеза. Предположим, что мы можем выполнить следующие химические реакции:
CO₂+H₂O ® H₂CO₃,
MgO+H₂ ® Mg+H₂O,
C+O₂ ® CO₂.
Можно ли получить (и в какой последовательности) H₂CO₃, если мы имеем MgO, C, H₂ и O₂?

2.16 Задача об опоздавшем автобусе ([Г84]). Даны следующие посылки:

1. Если Билл поедет на автобусе, то он потеряет свое место, если автобус опоздает.

2. Билл не сможет вернуться домой, если он потеряет свое место и будет чувствовать себя подавленным.

3. Если Билл не получит работу, то он будет чувствовать себя подавленным и не сможет вернуться домой.

Какие из следующих предложений верны, если верны указанные выше посылки? Дайте доказательства истинных предложений и контрпримеры к остальным.

а) Если Билл поедет на автобусе, то Билл потеряет работу, если автобус опоздает.

б) Билл получит работу, если он потеряет свое место и сможет вернуться домой.

в) Если Билл не потеряет своего места, то он не сможет вернуться домой и не получит работы.

г) Билл будет чувствовать себя подавленным, если автобус опоздает или он потеряет свое место.

2.17 Записать в форме предиката утверждения: “Если два объекта из М обладают свойством Р, то они совпадают”; “По крайней мере один студент решил все задачи”; “Каждую задачу решил по крайней мере один студент”.

2.18 ([П82]) Один из афоризмов Козьмы Пруткова звучит так: “Нет столь великой вещи, которую не превзошла бы величиной еще большая; нет вещи столь малой, в которую не вместилась бы еще меньшая”. Записать в форме предиката афоризм используя атомный предикат Р(х,у): “х больше у”. Являются ли обе части афоризма тождественными с точки зрения передаваемой информации?

2.19 Выразить с помощью предикатов: а) утверждение “Один и только один объект обладает свойством Р ” и его отрицание; б) утверждение “По меньшей мере два объекта обладают свойством Р ” и его отрицание.

2.20 В книге [Г84] изучаются проблемы корректности программ с помощью утверждений о соотношениях между программными переменными в различных состояниях программы. Выразить с помощью предикатов следующие утверждения:

(а) Все элементы массива b[j:k] нулевые.

(b) Ни один элемент массива b[j:k] не нулевой.

(c) Некоторые элементы массива b[j:k] нулевые.

(d) Все нулевые элементы массива b[0:n-1] находятся в b[j:k].

(e) Значения массива b[0:n-1] расположены в возрастающем порядке.

2.21 [Н81] Определение предела числовой последовательности в словесной формулировке имеет вид: “Число А является пределом последовательности (а_n), если и только если для всякого положительного числа e существует такое число N, что для всякого n, большего N, |a_n-A|<e”. В виде предиката это запишется так: A=lim a_n Û ("eÎR₊)($N)("n)[n>NÞ|a_n-A|<e]. Получить необходимое и достаточное условие истинности утверждения “Число А не является пределом последовательности (а_n)”, построив его в форме предиката, а потом сформулировать словесно.

2.22 Доказать методом резолюции, что если Кащей бессмертен, то он не человек.

2.23 Доказать справедливость рассуждения: “Иван и Петр - братья. Братья имеют одну фамилию. Петр имеет фамилию Сидоров. Следовательно, Иван тоже имеет фамилию Сидоров”?
Указание. Ввести предикаты: Б(х,у): х и у –братья, Ф(х,f): х имеет фамилию f. Факты: F1::Б(х,у), F2::("x)("у) [Б(х,у) Þ ("f) Ф(x,f) Þ Ф(y,f)]. F3::Ф(П,С). Следствие, подлежащее доказательству: R:: Ф(И,С). Какoе дополнительнoе утверждениe должнo быть явно сформулированo для доказательства?

2.24 Проверить, можно ли из следующей совокупности фактов:
(F1) Марк был римлянином;
(F2) Цезарь был диктатором;
(F3) Те римляне которые ненавидели диктатора, пытались убить его;
(F4) Римляне либо были преданы диктатору, либо ненавидели его;
(F5) Марк не был предан Цезарю
вывести доказательство того, что Марк пытался убить Цезаря.

2.25 Проверить правильность рассуждения: “Никакой торговец подделанной водкой не покупает ее для себя. Некоторые люди, покупающие для себя подделанную водку, глупы. Следовательно, некоторые глупые люди не являются торговцами подделанной водкой”.

Указание. Пусть: Т(х): х – торговец подделанной водкой, П(х): х - покупает подделанную водку для себя, Г(х): х – глупый человек. Схема рассуждения: F1:: Ø($x:Т(x))П(x); F2::($x:П(x))Г(х); R::($x:Г(x))ØТ(х)

2.26. Выполнить вручную программу на языке ПРОЛОГ:

дедушка(Х,У)Üотец(Х,V), отец(V,У)

отец(Чарльз, Вильям)

отец(Джереми, Пол)

отец(Вильям, Генри)

отец(Чарльз, Смит)

отец(Смит, Майк)

отец(Смит, Джереми)

?дедушка(Чарльз, Z)

которая должна найти всех внуков Чарльза. Ответом является каждая конкретизация переменной Z, полученная алгоритмом унификации на пути построения пустой резольвенты.

2.27. Вычисление резольвент для программы на ПРОЛОГЕ следует определенной стратегии, при которой вычисляются резольвенты, порождаемые целью или ее потомком и каким-либо правилом или фактом, которые просматриваются последовательно сверху вниз. Можно ли утверждать, что ответ на вопрос программы отрицателен, если не найдена пустая резольвента, хотя очевидно, что при этой стратегии строятся не все возможные резольвенты.

2.28 Построить программу на языке Пролог и провести ручную прокрутку ее для решения следующей проблемы: " Известно, что каждый предок любит своего потомка. А - дедушка В, а В и С - братья. Доказать, что А любит С".

2.29 Содержание объявления в газете “Экстра-Балт” No 31 от 15 августа 1966 года: “Выношу благодарность доктору Сан-Ал-Мину за возвращенное мне счастье, дай Бог ему здоровья” наводит на размышление о том, что это фальшивка. Действительно, если это не фальшивка, то Сан-Ал-Мин, по-видимому, действительно хороший доктор. Но если он такой хороший, то он может лечить всех. Однако, для его собственного здоровья доктору Сан-Ал-Мину необходима божественная помощь, следовательно сам себя доктор Сан-Ал-Мин вылечить не может. Следовательно, это объявление - фальшивка. Формализуйте это рассуждение и докажите, что данное объявление - фальшивка.

2.30 Выполните вручную программу 3 сортировки списка для цели ?Sort([23 5 7], S).

2.31 Выполните вручную программу Пролога анализа схемы полусумматора для целей ?half_add(A,B,0,1), ? half_add(А,В,Х,Х), ? half_add(X,X,X,1).

ЛИТЕРАТУРА

[ЧЛ83] Ч.Чень, Р.Ли. Математическая логика и автоматическое доказательство теорем // М., “Наука”, 1983.

[Ш88] С.И.Шапиро. Решение логических и игровых задач // М., “Радио и связь”, 1984.

[K78] С. Клини. Математическая логика // М., “Мир”, 1978

[C85] Р. Смаллиан. Принцесса или тигр // М., “Мир”, 1985

[R65] J.A.Robinson. A Machine-Oriented Logic Based on the Resolution Principle // Journal of the ACM - vol.12, 1965, No 1.

[Н81] И.Л.Никольская. Математическая логика // М., “Высшая школа”, 1981

[П68] Ю.Е.Пензов. Элементы математической логики и теории множеств // Изд-во Саратовского Университета, 1968

[П82] Д.А.Поспелов. Фантазия или наука. На пути к искусственному интеллекту // М., “Наука”, 1982,

[CL89] J. Carrol, D. Long. Theory of Finite Automata with Introduction to Formal languages // Prentice-Hall International, 1988, 438 p.

[Ч60] А.Черч. Введение в математическую логику // М., “Издательство иностранной литературы”, 1960

[Г84] Д.Грис. Наука программирования // М., “Мир”, 1984

[GL88] L. Goldschlager, A. Lister. Computer Science. A modern introduction // Prentice Hall, 1988, 330p.

[C87] W.F.Clocksin. Logic programming and digital circuit analysis // J. Logic Programming, 1987, 4, 59-82.

[PGM93] A.Pell, C.Goh, P.Mellor. Data + Understanding = Management // Hewlett-Packard Laboratories Technical Report, HPL-93-24, March, 1993