Логический вывод в Прологе

Логика предикатов и понятие логического вывода были разработаны в первой половине нашего века, но только в конце 60-х были поняты огромные возможности логического вывода для построения непроцедурных алгоритмов, тогда же и были разработаны методы резолюции, алгоритм унификации, и в конце концов язык логического программирования ПРОЛОГ. Основной вклад в логическое программирование был сделан Аланом Робинсоном (Alan Robinson), Алайном Колмерауером (Alain Colmeraurer) и Робертом Ковальски (Robert Kowalski), причем он был сделан сравнительно недавно. В этом языке исходное множество формул, для которого ищется пустая резольвента, представляется в виде так называемых “дизъюнктов Хорна”. Хорновские дизъюнкты - это формулы одного из трех типов:

отрицание : Ø(В1,...,Вn)

факт: А

импликация (правило): АÜ(В1,...,Вm),

где А, В₁, ... - литеры - атомные высказывания или предикаты с отрицаниями или без них в нормальной предваренной форме только с (подразумеваемыми) кванторами всеобщности для всех переменных. Как мы видели из предыдущих разделов, любую логическую формулу можно привести к такому виду. Факты можно рассматривать как импликации, не имеющие посылок (антецедентов). Отрицания - как импликации, не имеющие следствий (консеквентов). Поэтому все дизъюнкты Хорна - это формулы вида АÜ(В₁,...,В_m), которые просто являются другой записью импликации В₁&...&В_mÞА, и знак Ü здесь может читаться как "при условии, что". Все эти формулы представляются в виде дизъюнктов: ØВ₁Ú...ÚØВ_mÚА, или просто множеством литер {А,ØВ₁,...,ØВ_m}, поскольку знак дизъюнкции подразумевается. Именно к этим дизъюнктам и применяются последовательные шаги метода резолюции.

Таким образом, все задачи логического вывода можно формулировать, пользуясь только дизъюнктами Хорна, и все те задачи, которые являются в принципе разрешимыми, можно решить с помощью метода резолюции. Рассмотрим несколько примеров из [GL88].

Пусть в нотации, близкой языку ПРОЛОГ, записана программа:

Программа_1::

1: птица(Х) Ü откладывает_яйца(Х), имеет_крылья(Х)

2: рептилия(Х) Ü откладывает_яйца(Х), имеет_чешую(Х)

3: откладывает_яйца(ворона)

4: откладывает_яйца(питон)

5: имеет_чешую(питон)

6: имеет_крылья(ворона)

7:?птица(ворона)

В первой строке стоит правило, которое можно понять так: любое животное является птицей при условии, что оно откладывает яйца и имеет крылья. Очевидно, что это просто предикат в предваренной нормальной форме с опущенным квантором всеобщности (потому здусь и следует читать: любое животное). Этот предикат задан здесь одним дизъюнктом (птица(Х), Øотладывает_яйца(Х), Øимеет_крылья(Х)), где атомные предикаты дизъюнкта просто перечисляются через запятую вместо того, чтобы перечисляться через знак дизъюнкции. Вторая строка - это правило, аналогично определяющее класс рептилий. Третья строка - “откладывает_яйца(ворона)” - это, факт, который мы считаем истинным. Часто подобные факты присоединяются к программе из базы данных. Последняя строка - это утверждение-вопрос, истинность которого процессор языка ПРОЛОГ пытается проверить с помощью метода резолюции, пользуясь фактами и правилами.

Стратегии

В любом не «игрушечном» логическом выводе мы сталкиваемся с «комбинаторным взрывом» числа возможных резолюций, поскольку обычно база данных может содержать огромное множество фактов, не обязательно относящихся к данному конкретному вопросу, и построение всех возможных резольвентв этой базе данных бессмысленно. Поэтому при автоматизации логического вывода важнейшей проблемой является проблема выбора родительских дизъюнктов и их членов для унификации. Этот выбор должен выполняться так, чтобы пустая резольвента находилась скорейшим образом. Разработано несколько стратегий такого выбора, хотя общего метода, дающего оптимальное число шагов вывода для любой задачи, не существует. Например, в качестве одной из стратегий может применяться метод выбора на каждом шаге в качестве одного из родительских дизъюнктов такого дизъюнкта, который содержит только один дизъюнктивный член.

Выполнение программы на ПРОЛОГЕ следует другой стратегии: отрицание вопроса программы принимается за цель. Далее вычисляются резольвенты, порождаемые целью и каким-либо правилом или фактом, которые просматриваются последовательно сверху вниз. Если резольвента существует при наиболее общей унификации, она вычисляется. Если пустая резольвента с помощью такой стратегии не найдена, то ответ на вопрос отрицателен. В нашем примере резольвентой утверждений: Øптица(ворона) и птица(Х)Üоткладывает_яйца(Х),имеет_крылья(Х) является дизъюнкт, включающий отрицания двух утверждений: отладывает_яйца(Х) и имеет_крылья(Х). Эта пара становится новой целью, для которой снова ищется резольвента. Очевидно, что если в процессе вычислений найдена пустая резольвента, ответ на заданный вопрос утвердительный. Результатом программы на ПРЛОГЕ являются также и значения переменных, конкретизированные алгоритмом унификации в процессе вычислений - т.е. те значения параметров. при которых справедливо заключение. В примерах далее будем использовать прописные буквы для обозначения переменных, а строчные буквы - для имен конкретных объектов универсума.

Рассмотрим вычисление Программы 1:

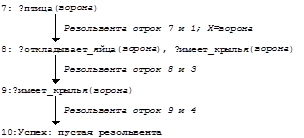
Получение пустой резольвенты означает успех вычисления. Фактически, стоящий перед атомным предикатом знак вопроса означает вхождение этого предиката в дизъюнкт со знаком отрицания, и каждый такой дизъюнкт представляет собой очередную цель, которую нужно достичь (как бы проверить ее истинность).

Рассмотрим вычисление этой же программы с другой целью: 7:?птица(Х), что означает "Существует ли (произвольная) птица?". Пользователя обычно интересует не только сам факт успешного вычисления программы, но и конкретное значение переменной Х, при котором это возможно:

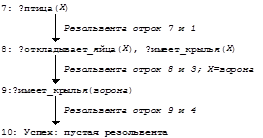
Заметим, что здесь цель вычисления была достигнута при нахождении единственного примера, который ему удовлетворяет. В общем случае может быть необходимо найти все такие конкретизации, удовлетворяющие цели, т.е. процессор Пролога должен пытаться найти все возможные резольвенты-продолжения. Рассмотрим следующий пример.

Программа_2::

1: Grandparent(X,Y) Ü Parent(X,Z), Parent(Z,Y)

2: Parent(elizabeth, charles)

3: Parent(charles, william)

4: Parent(charles, henry)

Содержательный смысл утверждений здесь очевиден. В качестве цели может быть выбрана любая из следующих:

5-а: ?Grandparent(elizabeth, henry);

5-b: ?Grandparent(elizabeth, V);

5-c: ?Grandparent(U, henry);

5-d: ?Grandparent(U, V).

Рассмотрим все возможные вычисления программы 2 при цели 5-d:

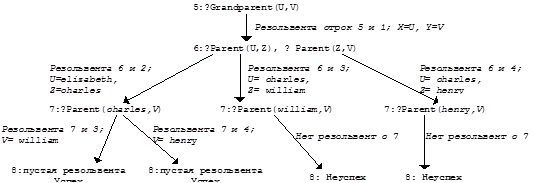
В качестве последнего примера из [GL88] рассмотрим логическую программу сортировки списка. Будем считать, что если у списка L выделены начальный элемент (голова) H и весь остальной список Т (хвост), то список L будем записывать как L=H:T.

Первый оператор логической программы сортировки списка определим как утверждение, которое определяет сортировку списка как результат подходящей вставки головы списка в отсортированный хвост списка:

1. Sort(H:T,S)ÜSort(T,L),Insert(H,L,S)

Смысл этого утверждения следующий: "список S является результатом сортировки списка H:T, если L является результатом сортировки списка T и S есть результат вставки элемента H в подходящее место списка L". Это определение справедливо для всех списков, кроме пустых; этот частный случай можно учесть указанием конкретного факта: пустой список уже отсортирован:

2. Sort([],[])

Теперь мы должны определить, что означает операция Insert(Х,L,S)вставки элемента Х в отсортированный список L с получением отсортированного списка S. В случае, если этот элемент Х предшествует первому элементу списка L, то список S строится добавлением Х в качестве новой головы L:

3. Insert(X,H:T,X:H:T) Ü Precedes(X,H)

Это утверждение имеет следующий смысл: "Если элемент X предшествует по порядку элементу Н, то результатом вставки X в отсортированный список H:T является отсортированный список X:H:T".

Если элемент H предшествует элементу X в списке H:T, то этот случай можно описать так:

4. Insert(X,H:T,H:T1) Ü Precedes(X,H), Insert(X,T,T1)

что можно интерпретировать так: "Результатом вставки X в отсортированный список H:T является список H:T1, если H предшествует X и T1 является отсортированным списком, получаемым после вставки X в отсортированный список T".

Кроме того, следует определить вставку элемента в пустой список:

5. Insert(X,[],[X]).

Таким образом, полная программа сортировки списка имеет пять операторов - утверждений:

Программа_3::

1. Sort(H:T,S) Ü Sort(T,L), Insert(H,L,S)

2. Sort([],[])

3. Insert(X,H:T,X:H:T) Ü Precedes(X,H)

4. Insert(X,H:T,H:T1) Ü Precedes(X,H), Insert(X,T,T1)

5. Insert(X,[],[X]).

Эту программу мы можем использовать многими различными способами, задавая различные цели. Например, "?Sort([dog cat pig], [cat dog pig])". При этой цели вычисление проверит, действительно ли список [cat dog pig] является отсортированной версией списка [dog cat pig]. При цели: "?Sort([dog cat pig], S)" вычислитель Пролога поместит в переменную S отсортированный список [dog cat pig]. При цели: "?Sort(S, [cat dog pig])" в переменную типа список S будут подставляться все перестановки элементов отсортированного списка [dog cat pig].