МЕХАНИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАБОТЫ КОЛОННЫ НАСОСНЫХ ШТАНГ

Принципы построения лабораторной механической модели штанговой глубиннонасосной установки рассмотрены в работе Г.И. Иокима. Однако предложенная модель адекватна вертикальной

скважине, где трение между штангами и трубами пре­небрежимо мало. Рассмотрим вопросы моделирования работы на­сосных штанг в наклонно направленных скважинах.

Моделирование работы глубиннонасосный установки включает:

1) моделирование вынужденных колебаний штанговой колонны;

2) моделирование напряженного состояния штанговой ко­лонны.

Для упрощения задачи деформации насосно-компрессорных труб влияние газа на работу установки, образование эмульсии в трубах, в насосе и др. не учитываются. Таким образом, за­дача сводится к рассмотрению упругих явлений в длинном стержне, совершающем вынужденные продольные колебания и под­верженном нагрузкам, аналогичным тем, которые испытывает ко­лонна насосных штанг.

Геометрическое подобие

При моделировании колонны насосных штанг воспользуемся известным методом - аффинным подобием, т.е. введем для раз­меров поперечного сечения один масштаб (/О, а для длины -другой (К₂). Тогда

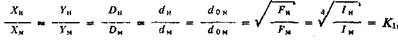(6)

где X, Y - координаты точки; D - внутренний диаметр НКТ; d,d₀ - диаметр тела и муфты штанг; F - площадь поперечного се­чения штанг; I - момент сопротивления поперечного сечения.

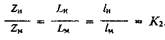(7)

где Z - координата точки; L - длина колонны штанг; l - длина штанги.

Разделив каждое соотношение полученных равенств на d_н/d_м и введя обозначения Х_Н/Х_М = λ_Х и т.д., получим

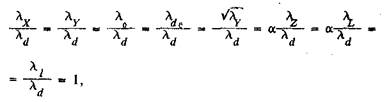(8)

где α = K₁ / K₂

Моделирование вынужденных колебаний штанговой колонны

Для получения критериев подобия вынужденных колебаний до­пускаем, что штанговая колонна ведет себя как абсолютно твердое тело, так как закон движения головки балансира мало зависит от деформации штанг. При этом дифференциальным урав­нением движения штанговой колонны является следующее:

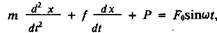(9)

где т - масса штанговой колонны; f - коэффициент трения штанг о трубы; Р - сопротивление в насосе; F₀sinwt - возму­щающая сила, действующая на колонну штанги.

Опустив знаки дифференцирования, поделим все члены урав­нения на один из его членов. Получаем безразмерные комплексы

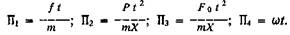
Как известно, критерии подобия, если в них вместо переменных величин ввести соответствующие начальные условия, дают до­статочные условия подобия двух систем. Если 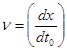и Х₀ - соответственно скорость и координата в начальный момент времени, то достаточными условиями подобия являются:

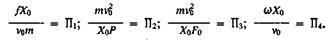
Очевидно, вместо текущих значений координат, скорости и вре­мени можно подставить некоторые их характерные значения, на­пример, длину хода головки балансира S, максимальную ско­рость v_max и число ходов головки балансира n.

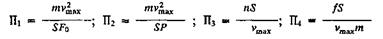
или

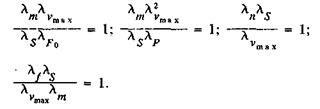(10)

Преобразованием выражений (10) можно получить следующие критерии подобия:

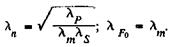
Для моделирования напряженного состояния штанговой колон­ны воспользуемся критериями подобия, полученными в работе П.В. Балицкого, описывающими напряженное состояние бурильных труб, так как они являются общими и для колонны насосных штанг. Натура и модель выполнены из разных материалов.

Критерии подобия напряженного состояния:

а) растяжение (сжатие)

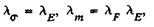
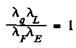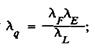или (12)

б) изгиб

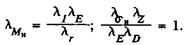
Для того чтобы модель и натура были подобны по напряжен­ному состоянию от изгиба, необходимо выполнение условия

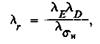(13)

где 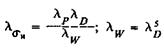или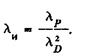

Тогда

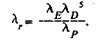(14)

Радиус искривления ствола скважины определяют по формуле

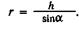(15)

Основные критерии подобия моделирования работы штанговой колонны в наклонно направленных скважинах сведены в табл. 5. Как видно из таблицы, даже применение материалов с различ­ными физико-химическими свойствами не позволяет добиться по­добия по весу 1 м штанг. Наиболее подходящий материал для моделирования штанговой колонны - латунная проволока диа­метром 0,1 см. Недостающий вес 1 м может быть дополнен ла­тунными втулками с зазором, насаженными на проволоку.

Таблица 5