Моделей в рамках ФСА
Использование оптимизационных
Рассмотрим один из вариантов ЭММ, не затрагивая различных аспектов построения, выбора и сравнительного анализа самих моделей, поскольку все это входит в задачи совсем других курсов. В соответствии с методикой ФСА в качестве критерия эффективности в модели можно использовать комплексный показатель качества. В самом простом варианте – это линейная свертка критериев степени достижения отдельных функциональных свойств объекта, взвешенных в соответствии со значимостью отдельных функций [1]. В соответствии с той же методикой другим важнейшим показателем является стоимостная оценка всего проекта.
Введем следующие обозначения:
L – множество уровней структуризации функций;
Jl – множества функций l-го уровня;
vlj – множества вариантов реализации j-й функции l-го уровня;
rlj – значимость j-й функции l-го уровня;
yljv – степень исполнения j-й функции l-го уровня при v-м варианте реализации;
yljэ – эталонное значение степени исполнения j-й функции l-го уровня;
yljп – пороговое значение степени исполнения j-й функции l-го уровня;
xljv – переменная выбора варианта реализации j-й функции l-го уровня:
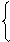 1 – если выбирается v-й вариант реализации j-й функции l-го уровня;
1 – если выбирается v-й вариант реализации j-й функции l-го уровня;
xljv =
0 – в противном случае;
при этом 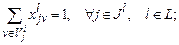
cljv – затраты на осуществление j-й функции l-го уровня при
v-м варианте реализации;
Qоб – комплексный показатель качества;
P – сумма, необходимая для реализации проекта;
Pmax – максимальная сумма, выделяемая для реализации проекта.
Тогда ЭММ выбора наилучшего варианта реализации проекта (модернизации объекта при корректирующей форме ФСА) можно формально представить в следующем виде:
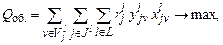 (2.1)
(2.1)
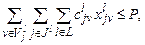 (2.2)
(2.2)
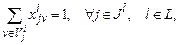 (2.3)
(2.3)
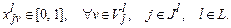 (2.4)
(2.4)
Линейный функционал (2.1), выражающий обобщенный критерий качества, имеет ряд недостатков. Основным из них является возможность выбора вариантов исполнения отдельных функций с недопустимыми качественными характеристиками.
Альтернативным критерием может служить сумма квадратов отклонений выбираемых вариантов реализации отдельных функций от некоторых эталонных значений.
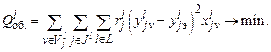 (2.5)
(2.5)
При использовании же критерия (2.1) следует добавить ограничения на пороговые (минимальные) значения уровней исполнения отдельных функций:
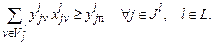 (2.6)
(2.6)
Вариантов реализации ЭММ на основе условий (2.1–2.6) может быть несколько. Кроме задаваемого непосредственно условиями (2.1)–(2.4), (2.6), можно рассмотреть вариант ЭММ с использованием в качестве критерия эффективности минимума затрат (2.2) на осуществление проекта при заданных качественных характеристиках [при ограничениях на показатели (2.1) и (2.6)]. Третий вариант – использование двух критериев эффективности (2.1) и (2.2). В этом случае определяются Парето-оптимальные варианты реализации проекта с последующим выбором окончательного варианта лицом, принимающим решения (ЛПР) в соответствии со своей системой предпочтений. Разновидностью этого же подхода является параметрический анализ модели (2.1)–(2.4), (2.6), где в качестве параметра рассматривается P – цена проекта, при соблюдении дополнительного ограничения:
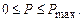 (2.7)
(2.7)
В результате параметрического анализа ЭММ генерируется множество вариантов решений, при этом окончательный выбор единственного из них также остается за ЛПР. Еще одной разновидностью использования одновременно двух критериальных показателей является их свертка. В ФСА, в частности, используется отношение «значимость/затраты» («качество/затраты») или «затраты/значимость» [1]. Такая свертка будет выглядеть следующим образом:
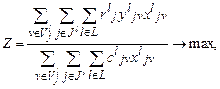 или
или 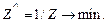
В реальных условиях ЭММ могут дополняться ограничениями на количественные (ресурсные) характеристики объекта (проекта), что существенно расширяет возможности методик ФСА, как средств анализа и разработки управленческих решений. В связи с этим следует отметить явную связь ФСА через посредство ЭММ с методами оптимального проектирования.
Рассмотрим численный пример применения методики ФСА с использованием изложенного подхода.
Дата добавления: 2020-10-25; просмотров: 425;











