Модулированные сети могут одновременно передавать телепрограммы, речь, двоичные данные и т. п. 5 глава
Рис. 2.4. Представление чисел с плавающей точкой
В современных ЭВМ используются обе формы представления чисел.
2.1.1.1 Представление команд в ЭВМ
Программа работы машины, определяющая процесс обработки информации в ЭВМ, состоит из последовательности команд.
Под командой ЭВМ понимается информация, обеспечивающая выработку управляющих сигналов для выполнения машиной определенного действия.
Поле команды состоит из двух частей: операционной и адресной. В операционной части указывается код операции (КОП), определяющий действие (арифметическое или логическое), которое должна выполнить машина. Адресная часть команды содержит адреса операндов (величин), участвующих в операции. Под адре-сом "А" понимается номер (цифровой код) машинного слова (или другого поля памяти ЭВМ), где записана необходимая для выполнения команды информация. Количество указываемых в команде адресов может быть различным. Соответственно числу адресов определяются следующие форматы команд: одноадресные, двухадресные, трехадресные и четырехадресные (рис. 2.5).
Рис. 2.5. Форматы команд ЭВМ
Трехадресная команда, выполняющая, например, операцию сложения, должна содержать код операции сложения и три адреса. Действия, выполняемые такой командой, определяются примерно следующей последовательностью:
1) взять число, хранящееся по первому адресу;
2) взять число, хранящееся по второму адресу, и сложить его с первым числом;
3) результат сложения записать по третьему адресу.
В случае двухадресной команды третий адрес отсутствует, и результат можно записать либо по второму адресу (с потерей информации, которая была там записана), либо оставить в сумматоре, где производилась операция сложения. Тогда для освобождения сумматора требуется дополнительная команда перезаписи числа по требуемому адресу. При сложении двух чисел, хранящихся по адресам A1 и A2, с записью результата, например, в A1 с использованием двухадресной команды, требуется уже четыре команды:
1) вызов в сумматор числа, хранящегося по адресу A1;
2) вызов числа, хранящегося по адресу A2, и сложение его с первым числом;
3) стереть число по адресу A1;
4) запись результата по адресу A1.
Таким образом, чем меньше адресность команд ЭВМ, тем большее число команд требуется для составления одной и той же программы работы машины.
Увеличивая адресность ЭВМ, приходиться увеличивать длину машинного слова, чтобы отвести в нем необходимые поля для адресной части команд. С увеличением объема памяти ЭВМ увеличивается длина поля, необходимого для одного адреса. В то же время не все команды полностью используют адресные поля. Например, для команды записи числа по заданному адресу требуется только одно адресное поле.
2.1.2 Системы счисления
Способ представления чисел посредством числовых знаков (цифр) называется системой счисления. Правила записи и действий над числами в системах счисления, используемых в цифровой вычислительной технике, определяют арифметические основы цифровых ЭВМ.
Компоненты системы счисления:
1. Основание системы счисления - количество различных цифр (символов), используемых для представления числа.
2. Алфавит системы счисления - символы и цифры, используемые для написания всех разрядов числа.
3. Правила записи и чтения чисел.
Различают два основных вида систем счисления: непозиционные и позиционные.
Непозиционные системы счисления.
Непозиционные системы счисления характеризуются тем, что значение числа, выражаемое совокупностью цифр, определяется только конфигурацией цифровых символов и не зависит от места их положения. Классическим примером непозиционной системы является римская система счисления. Например: ХIX; XXIII.
Позиционные системы счисления.
Наибольшее распространение получили позиционные системы счисления, в которых значение любой цифры определяется не только конфигурацией ее символа, но и местоположением (позицией), которое она занимает в числе.
Среди позиционных систем различают однородные и смешанные (неоднородные) системы счисления.
В однородных системах количество допустимых цифр для всех позиций (разрядов) числа одинаково. Однородной позиционной системой является общепринятая десятичная система счисления (q = 10), использующая для записи чисел десять цифр от 0 до 9.
Примером смешанной системы счисления может служить система отсчета времени, где в разрядах секунд и минут используется по 60 градаций, а в разрядах часов - 24 градации и т. д.
Любое число A, записанное в однородной позиционной системе, может быть представлено в виде суммы степенного ряда:
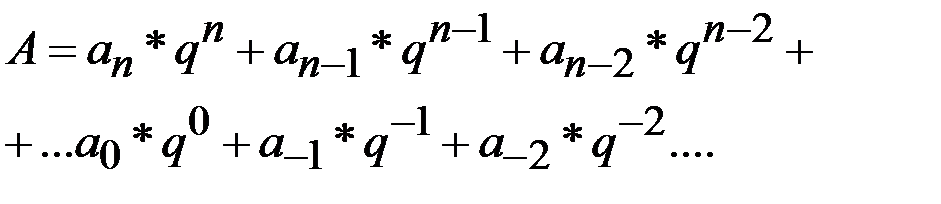 (2.1.)
(2.1.)
где q - основание системы счисления; ai - цифры системы счисления с основанием q; i - номер (вес) позиции (разряда) числа.
Может быть реализовано бесконечное множество различных систем счисления. В цифровых вычислительных машинах в основном используются однородные позиционные системы. Кроме десятичной системы счисления в ЭВМ находят широкое применение системы с основанием q, являющиеся степенью числа 2, а именно: двоичная, восьмеричная, шестнадцатеричная системы счисления.
При совместном использовании различных систем счисления после записи числа может указываться основание системы, например: 347,4210; 11012; 2358 и т. д.
2.1.2.1 Десятичная система счисления
В соответствии с формулой (2.1) позиция цифры в числе определяет степень числа с основанием 10, на которое эта цифра умножается.
Например: число 534,79 можно представить как
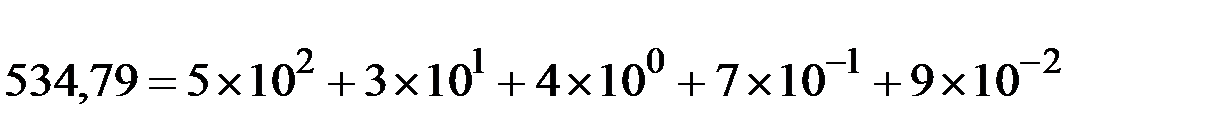 .
.
В одном разряде может быть представлено десять чисел от 0 до 9. Прибавление единицы к старшей цифре разряда (цифре 9) означает перенос единицы в старший разряд, т. е. для записи числа 10 и больших чисел требуется два и более разрядов. Число N = m Ч q p, где m - мантисса числа (m < 1); p - порядок; q - основание системы счисления, представляется в виде единицы в старшем разряде с последующими p нулями. Например, N = 104 = 10 000.
Это правило распространяется на все однородные позиционные системы счисления.
2.1.2.2 Двоичная система счисления
Основание системы q = 2. Для записи чисел используются две цифры: 0 и 1. Старший цифрой разряд является 1, поэтому в двоичной системе 1 + 1 = 10, так как прибавление единицы к старшей цифре данного разряда дает перенос единицы в старший разряд.
Каждое последующее число больше данного на единицу, получается в результате прибавления единицы в младший разряд с соблюдением правил сложения в двоичной системе счисления (табл. 2.1, 2.2).
Анализируя данные в таблице 2.1 следует отметить, что разряды в двоичной системе заполняются очень быстро. В силу этого для записи числа в двоичной системе счисления требуется значительно больше разрядов, чем в десятеричной. Число 2 и большие числа в двоичной систем счисления записываются в двух и более разрядах. Согласно ранее рассмотренному правилу число 2 = 21 записывается как 10, число 4 = 22 - как 100 и т. д.
Таблица 2.1
| Числа | Числа | |||||||||||||||
| деся-тичные | двоичные | восьмеричные | шестнадца-теричные | десятичные | двоич-ные | восьмеричные | шестнадца-теричные | |||||||||
| A B C D E F | ||||||||||||||||
Двоичная система счисления является основной системой представления информации в современных ЭВМ. Почти все вычислительные машины используют либо непосредственно двоичную систему счисления, либо двоичное кодирование какой-либо другой системы счисления, например, десятичной (двоично-десятичный код). Это объясняется тем, что элементы вычислительной машины, средства хранения информации, различающие два устойчивых состояния (0 и 1), наиболее просты в реализации и надежны в работе. Немаловажное значение имеет также простота реализации правил двоичной арифметики в ЭВМ (табл. 2.2).
Таблица 2.2
| Сложение | Вычитание | Умножение | |||||
| 0 Ч 0 0 Ч 1 1 Ч 0 1 Ч 1 | |||||||
При выполнении арифметических действий в двоичной системе счисления следует помнить, что единица является старшей значащей цифрой двоичного разряда.
Пример.
Выполняя в заданном разряде вычитание из нуля единицы, следует занять единицу из старшего значащего разряда. В результате в младшем разряде образуются две единицы. Операция умножения сводится к многократному сложению и сдвигу. При выполнении деления используются правила умножения и вычитания.
2.1.2.3 Восьмеричная система счисления
Основание системы q = 8. Для записи чисел используется восемь цифр от 0 до 7. В силу того что основание восьмеричной системы является третьей степенью числа 2, то для представления одного восьмеричного разряда требуется три значащих двоичных разряда (триада). Таким образом, для записи чисел в восьмеричной системе счисления требуется в 3 раза меньше разрядов, чем в двоичной системе (табл. 2.1).
Восьмеричная система счисления играет в ЭВМ вспомогательную роль и используется для компактной записи двоичных кодов чисел машинных команд ЭВМ в различных периферийных устройствах и устройствах подготовки данных. Перевод чисел из двоичной системы счисления в восьмеричную и наоборот осуществляется по триадам согласно второму столбцу таблицы 2.1 (первые восемь строк, неполные триады дополняются слева незначащими нулями). Разбиение двоичного числа на триады осуществляется влево и вправо от запятой, отделяющей целую часть числа от дробной. Если крайние триады получаются неполными, то они дополняются нулями.
Пример.
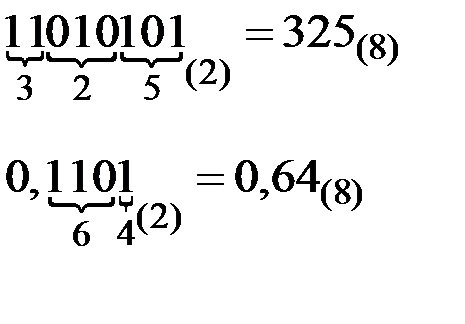
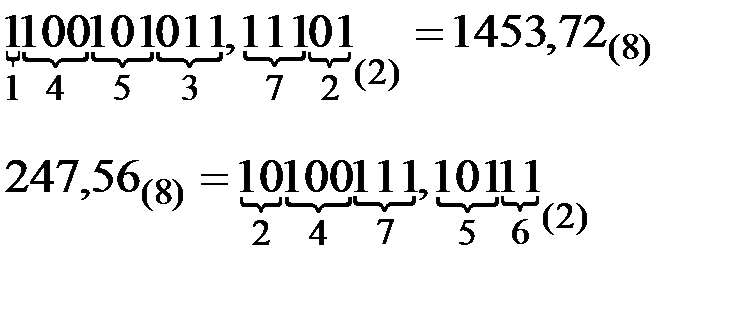
2.1.2.4 Шестнадцатеричная система счисления
Основание системы q = 24 = 16. Для записи чисел исполь-зуются шестнадцать цифр, из них первые десять - известные цифры от 0 до 9. В качестве дополненных цифр используются заглавные латинские буквы A, B, C, D, E и F (табл. 2.1).
Назначение шестнадцатеричной системы счисления аналогично восьмеричной: компактная запись двоичных кодов чисел и команд. Одному шестнадцатеричному разряду числа соответствует четыре двоичных разряда (тетрада), т. е. шестнадцатеричная система позволяет сократить длину записи числа по сравнению с двоичной в 4 раза.
Перевод чисел из двоичной системы в шестнадцатеричную систему и обратно осуществляется по тетрадам аналогично двоично-восьмеричному переводу (табл.2.1). Неполные тетрады дополняются нулями.
Пример.
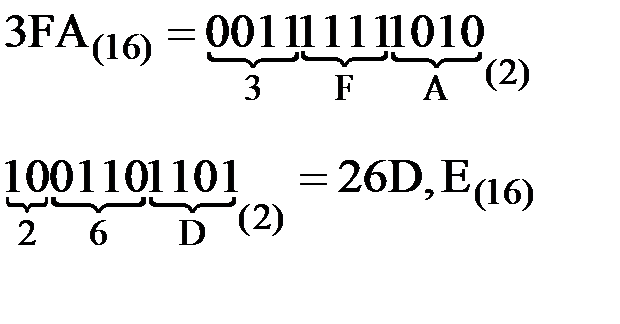
2.1.3 Элементы математической логики
Для описания логики функционирования аппаратных и программных средств ЭВМ используется алгебра логики, или булева алгебра (по имени ее создателя Дж. Буля).
Булева алгебра оперирует с логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые соответственно 1 и 0. Как отмечалось выше, основной системой счисления в ЭВМ является двоичная система, в которой также используются цифры 1 и 0. Таким образом, одни и те же устройства ЭВМ могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных. Это обусловливает сравнительную простоту схемной реализации процесса обработки информации в ЭВМ.
Совокупность значений логических переменных x1, x2, ..., xn называется набором переменных.
Набор логических переменных удобно изображать в виде n-разрядного двоичного числа, каждый разряд которого равен значению одной из переменных. Из таблицы 2.1 видно, что количество возможных наборов в n двоичных разрядах равно 2n.
Логической функцией от набора логических переменных (аргументов) f(x1, x2 ..., xn) называется функция, принимающая только два значения: истина или ложь.
Область определения логической функции конечна и зависит от числа возможных наборов аргументов. Любая логическая функция может быть задана с помощью таблицы истинности, где в левой части записываются возможные наборы аргументов, а в правой - соответствующие им функции.
В случае большого числа аргументов табличный способ задания логической функции становится громоздким и теряет наглядность. Так, уже для шести логических аргументов понадобится таблица в 64 строки, поэтому логические функции удобно выражать через другие более простые логические функции одной или двух переменных, описываемые с помощью простых таблиц.
Совокупности таких элементарных логических функций (или логических операций), с помощью которых можно выразить логическую функцию любой сложности, называются функционально полными системами логических функций.
В этой системе определены три элементарные логические операции: инверсия (отрицание), конъюнкция (логическое умножение) и дизъюнкция (логическое сложение).
Логические переменные, объединенные знаками логических операций, составляют логические выражения.
При вычислении значения логического выражения определено следующее старшинство выполнения логических операций: сначала выполняется инверсия, затем конъюнкция и в последнюю очередь - дизъюнкция.
Для изменения указанного порядка используются скобки.
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логи-ческих выражений.
1. Коммутативный закон: x1 V x2 = x2 V x1,
x1 Ч x2 = x2 Ч x1.
2. Ассоциативный закон: x1 V (x2 V x3) = (x1 V x2) V x3,
x1 Ч (x2 Ч x3) = (x1 Ч x2) Ч x3.
3. Дистрибутивный закон: x1 Ч (x2 V x3) = x1 Ч x2 V x1 Ч x3.
4. Правила де Моргана (теорема двойственности).
5. Правила операций с константами 0 и 1.
6. Правила операций с переменной и ее инверсией.
7. Закон поглощения.
8. Закон идемпотентности.
9. Закон двойного отрицания.
2.1.4 Методы перевода чисел из одной системы счисления
в другую
2.1.4.1 Метод прямого замещения
Перевод чисел из двоичной системы счисления в систему с основанием, являющимся степенью числа 2, и наоборот не вызывает трудностей. Это в частности стало причиной широкого применения в ЭВМ восьмеричной и шестнадцатеричной систем счисления. Однако может возникнуть задача перевода чисел из одной системы счисления в другую с произвольными основаниями. В этом случае необходимо воспользоваться общими правилами перевода, которые основаны на определении однородной позиционной системы счисления (2.1).
Число в системе счисления с основанием q1 расписывается по формуле (2.1) и вычисляется сумма ряда, при этом арифметические действия выполняются по правилам системы счисления с основа-нием q2.
Следуя этому правилу, легко перевести числа из двоичной и восьмеричной систем счисления в десятичную.
Пример.
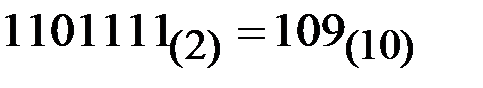
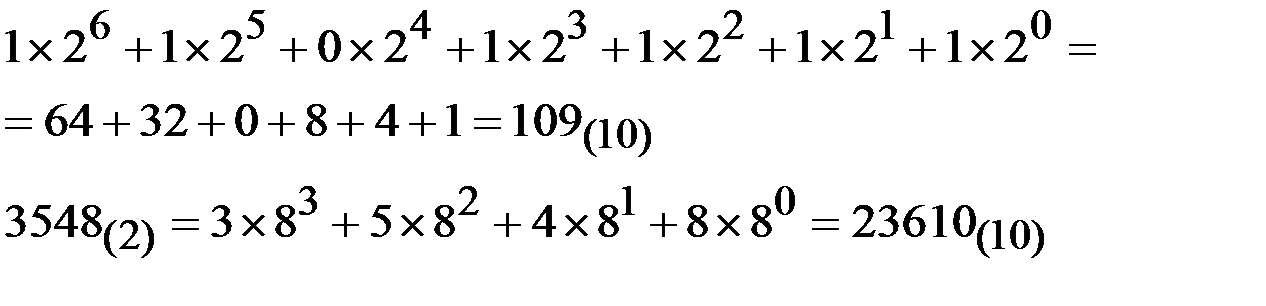
Можно также в отличие от ранее рассмотренного метода перевести числа из двоичной системы в восьмеричную, но для этого необходимо вычислять сумму ряда (2.1) по правилам восьмеричной арифметики. При переводе больших двоичных чисел в десятичные для его упрощения, целесообразно сначала перевести их по триадам в восьмеричные, а затем из восьмеричных в десятичные.
Пример.
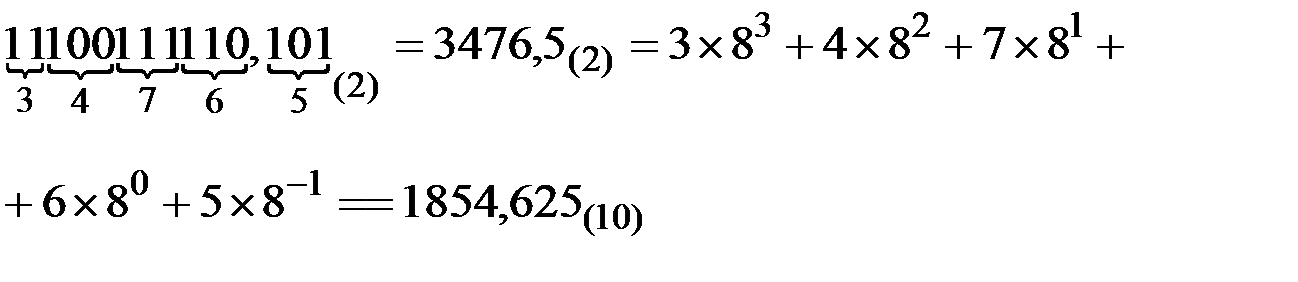
2.1.4.1 Метод деления
Если q1 > q2, используются два правила: для целых и дробных чисел.
Если переводятся целые числа, то необходимо последовательно делить число в системе q1 на основание системы q2 до тех пор, пока не останется остаток, меньший или равный q2-1. число в основании q2 записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример.
Для перевода больших десятичных чисел в двоичную систему счисления рекомендуется перевести их в восьмеричные, а затем расписать по триадам.
2.1.4.1 Метод умножения
Пример.
При переводе дробных чисел необходимо последовательно умножать число в системе q1 на основание системы q2, отделяя после каждого умножения целую часть произведения. Число в системе q2 (после точки) записывается как последовательность полученных целых частей произведения. Умножение производится до тех пор, пока дробная часть произведения не станет равной нулю или определенной степени точности.
При переводе смешанных чисел отдельно переводятся целая и дробная части, записываемые затем совместно.
2.2 Структурная схема ПЭВМ
2.2.1 Состав и технические характеристики ПЭВМ
2.2.1.1 Понятие архитектуры
Архитектура компьютера обычно определяется совокупностью ее свойств, существенных для пользователя. Основное внимание при этом уделяется структуре и функциональным возможностям машины, которые можно разделить на основные и дополнительные (рис. 2.6).
Основные функции определяют назначение ЭВМ: обработка и хранение информации, обмен информацией с внешними объектами.
Дополнительные функции повышают эффективность выполнения основных функций: обеспечивают эффективные режимы ее работы, диалог с пользователем, высокую надежность и др.
Названные функции ЭВМ реализуются с помощью ее компонентов: аппаратных и программных средств.
Функциональные возможности ЭВМ:
1) ввод программы и данных с клавиатуры, НГМД, НЖМД;
2) вывод программ и данных на экран видеомонитора, НГМД, НЖМД, принтер;
3) арифметическая и логическая обработка информации;
4) корректировка данных, редактирование программ;
5) хранение программ и промежуточных данных.
В состав типовой ЭВМ входят:
− центральный процессор;
− внутренняя память со своим интерфейсом;
− устройства ввода-вывода со своим интерфейсом, включающие устройства внешней памяти (НГМД, НЖМД), клавиатура, модуль отображения информации, принтер;
− интерфейс – совокупность средств сопряжения и связи устройств компьютера, обеспечивающая их эффективное взаимо-действие.
Рис. 2.6. Архитектура ЭВМ
2.2.1.2 Структура компьютера
Структура компьютера - это некоторая модель, устанавливающая состав, порядок и принципы взаимодействия входящих в нее компонентов (рис. 2.7).
Персональный компьютер (ПК) - это настольная или переносная ЭВМ, удовлетворяющая требованиям общедоступности и универсальности применения.
Рис. 2.7. Структурная схема персонального компьютера
Достоинствами ПК являются:
− малая стоимость, находящаяся в пределах доступности для индивидуального покупателя;
− автономность эксплуатации без специальных требований к условиям окружающей среды;
− гибкость архитектуры, обеспечивающая адаптивность к разнообразным применениям в сфере управления, науке, образовании, быту;
− "дружественность" операционной системы и прочего программного обеспечения, обусловливающая возможность работы с ней пользователя без специальной, профессиональной подготовки;
− высокая надежность работы.
2.2.2 Состав и назначение основных блоков и узлов ПЭВМ
2.2.2.2 Назначение основных устройств ЭВМ
1. Микропроцессор - это центральный блок ЭВМ, предназначенный для управления работой всех блоков машины и для выполнения арифметических и логических операций над информацией.
В состав микропроцессора входят:
− устройство управления (УУ), формирующее и подающее во все блоки машины в нужные моменты определенные сигналы управления (управляющие импульсы), обусловленные спецификой выполняемой операции и результатами предыдущей операции. МП формирует адреса ячеек памяти операндов, используемых выполняемой операцией, и передает эти адреса в соответствующие блоки ЭВМ;
− арифметико-логическое устройство (АЛУ) предназначено для выполнения всех арифметических и логических операций над числовой и символьной информацией;
− микропроцессорная память (МПП) служит для кратковременного хранения, записи и выдачи информации, непосредственно используемой в вычислениях в ближайшие такты работы машины;
− интерфейсная система микропроцессора реализует сопряжение и связь с другими устройствами ПК. Включает в себя внутренний интерфейс МП, буферные запоминающие регистры, схемы управления портами ввода-вывода (ПВВ) и системную шину.
2. Генератор тактовых импульсов генерирует последовательность электрических импульсов, их частота определяет тактовую частоту машины.
Промежуток времени между соседними импульсами определяет время одного такта работы машины или просто такт работы машины.
Частота генератора тактовых импульсов является одной из основных характеристик персонального компьютера и во многом определяет скорость его работы.
3. Основная память (ОП) предназначена для хранения и оперативного обмена информацией с прочими блоками машины.
ОП содержит два вида запоминающих устройств: постоянное запоминающие устройство (ПЗУ) и оперативное запоминающее устройство (ОЗУ).
ПЗУ служит для хранения неизменяемой (постоянной) программы и справочной информации, что позволяет оперативно только считывать хранящуюся в нем информацию (изменить информацию в ПЗУ нельзя). ПЗУ является энергонезависимым.
ОЗУ предназначено для оперативной записи, хранения и считывания информации (программ и данных), непосредственно участвующей в информационно-вычислительном процессе, выполняемом ПК в текущий период времени.
Главными достоинствами оперативной памяти являются ее высокое быстродействие и возможность обращения к каждой ячейке памяти отдельно (прямой адресный доступ к ячейке).
В качестве недостатка ОЗУ следует отметить невозможность сохранения информации в ней после выключения питания машины, т. е. энергозависимость.
4. Внешняя память относится к внешним устройствам ПК и используется для долговременного хранения любой информации, которая может когда-либо потребоваться для решения задач.
Во внешней памяти хранится все программное обеспечение компьютера. Она содержит разнообразные виды запоминающих устройств. Наиболее распространенными, имеющимися практически в любом компьютере, являются накопители на жестких (НЖМД) и гибких (НГМД) магнитных дисках.
В качестве устройства внешней памяти используются также запоминающие устройства: на кассетной магнитной ленте (стримеры), накопители на оптических дисках (CD-ROM - Compact Disk Read Only Memory - компакт-диск с памятью, только читаемой) и др.
5. Источник питания - это блок, содержащий системы автономного и сетевого энергопитания ПК.
6. Таймер - внутримашинные электронные часы, обеспечивающие при необходимости автоматический съем текущего момента времени (год, месяц, часы, минуты, секунды и доли секунд). Таймер подключается к автономному источнику питания - аккумулятору и при отключении машины от сети продолжает работать.
7. Внешние устройства (ВУ) - важнейшая составная часть любого вычислительного комплекса. Достаточно сказать, что стоимость ВУ иногда составляет 50-80 % стоимости всего ПК. От состава и характеристик ВУ во многом зависят возможность и эффективность применения ПК в системах управления и народном хозяйстве в целом.
ВУ ПК обеспечивают взаимодействие машины с окружающей средой: пользователями, объектами управления и другими ЭВМ. ВУ весьма разнообразны и могут быть классифицированы по ряду признаков.
По назначению ВУ можно разделить:
- на внешние запоминающие устройства (ВЗУ), или внешнюю память ПК;
- диалоговые средства пользователя;
- устройства ввода информации;
- устройства вывода информации;
- средства связи и телекоммуникации;
- средства мультимедиа.
Внешние запоминающие устройства были рассмотрены ранее.
Диалоговые средства пользователя включают в свой состав видеомониторы (дисплеи), реже пультовые пишущие машинки (принтеры с клавиатурой) и устройства речевого ввода-вывода информации.
К устройствам ввода информации относятся:
- клавиатура - устройство для ручного ввода числовой, текстовой и управляющей информации в ПК;
- графические планшеты (диджитайзеры) - для ручного ввода графической информации путем перемещения по планшету специального указателя (пера);
- сканеры (читающие автоматы) - для автоматического считывания с бумажных носителей информации и ввода в ПК машинописных текстов, графиков, рисунков, чертежей;
- манипуляторы (устройства указания): джойстик, мышь, трекбол (шар в оправе), световое перо и др. - для ввода графической информации на экран дисплея путем управления движением курсора по экрану с последующим кодированием координат курсора и вводом их в ПК;
- сенсорные экраны - для ввода отдельных элементов изображения, программ или команд с полиэкрана дисплея в ПК.
К устройствам вывода информации относятся:
- принтеры - печатающие устройства для переноса информации на бумажный носитель информации;
- графопостроители (плоттеры) - для вывода графической информации (графиков, чертежей, рисунков) из ПК на бумажный носитель;
Устройства связи и телекоммуникации используются для связи с приборами, другими средствами автоматизации и для подключения ПК к каналам связи.
Средства мультимедиа - это комплекс аппаратных и программных средств, позволяющих человеку общаться с компьютером, используя самые разные, естественные для себя среды: звук, видео, графику, тексты, анимацию и др.
К средствам мультимедиа относятся устройства речевого ввода и вывода информации, высококачественные видео- и звуковые платы, платы видеозахвата (videograbber), снимающие изображение с видеомагнитофона или видеокамеры и вводящие его в ПК; высококачественные акустические и видеовоспроизводящие системы с усилителями, звуковыми колонками, большими видеоэкранами. С большим основанием к средствам мультимедиа относят внешние запоминающие устройства большой емкости на оптических дисках, часто используемые для записи звуковой и видеоинформации.
Дополнительные схемы.
К системной шине и к МП ПК наряду с типовыми внешними устройствами могут быть подключены и некоторые дополнительные платы с интегральными микросхемами, расширяющие и улучшающие функциональные возможности микропроцессора: математический сопроцессор, контроллер прямого доступа к памяти, сопроцессор ввода-вывода, контроллер прерываний и др.
Математический сопроцессор широко используется для ускоренного выполнения операций над двоичными числами с плавающей точкой, двоично-кодированными десятичными числами для вычисления некоторых трансцендентных функций.
Математический сопроцессор имеет свою систему команд и работает параллельно с основным МП, но под управлением последнего. Ускорение операций происходит в десятки раз. Последние модели МП, начиная с МП 80486 DX, включают сопроцессор в свою структуру.
Дата добавления: 2016-05-31; просмотров: 1615;











