Амплитудно-модулированные сигналы
Модуляция по амплитуде без подавления несущей частоты.
В потенциометрической схеме с несимметричным питанием при дифференциальном включении двух резистивных датчиков выходное напряжение схемы равно
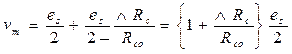
Если датчики линейны и чувствительность S постоянна во всем рабочем спектре частот измеряемой величины, то

т. е. vm изменяется в функции 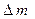 линейно.
линейно.
При питании указанной схемы синусоидальным напряжением 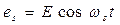 предыдущее соотношение преобразуется к виду
предыдущее соотношение преобразуется к виду
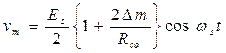
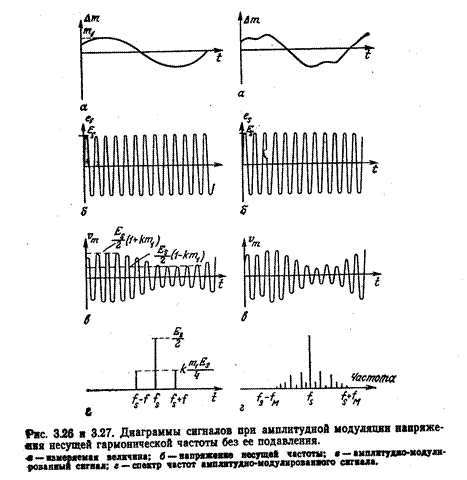
Если измеряемая величина изменяется по синусоидальному закону (рис. 3.26),
то 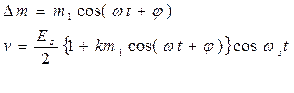
где , 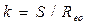 . a S — чувствительность датчика в динамическом режиме на частоте опоздания.
. a S — чувствительность датчика в динамическом режиме на частоте опоздания.
После элементарных тригонометрических преобразований можно записать:
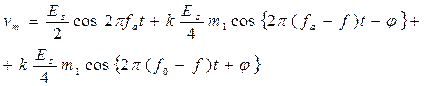
где 
Спектр напряжения vm (рис 3.26, г) содержит частоты 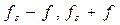 . В более общем случае (рис. 3.27), когда изменения измеряемой величины образуют сигнал сложной формы, который может быть представлен как результат наложения друг на друга большого числа гармонических составляющих
. В более общем случае (рис. 3.27), когда изменения измеряемой величины образуют сигнал сложной формы, который может быть представлен как результат наложения друг на друга большого числа гармонических составляющих
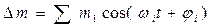 ,
,
получаем
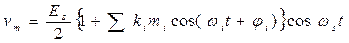 ,
,
где 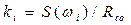 . Последнее выражение для vm можно преобразовать к виду
. Последнее выражение для vm можно преобразовать к виду
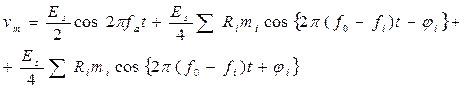 .
.
Спектр этого напряжения (рис. 3.27, г) содержит частоту fs питающего напряжения, называемую несущей частотой, нижнюю боковую полосу, образованную набором частотfs—fi, и верхнюю боковую полосу с частотами fs+fi.
Если fМ — верхняя граничная частота спектра измеряемой величины, то спектр выходного напряжения измерительной схемы простирается от fs—fм до fs+fм, Поэтому, чтобы передать спектр измеряемой величины, схемы обработки сигнала должны иметь полосу пропускания, равную, по крайней мере, 2fм с центральной частотой fs.
Если питающее напряжение не гармоническое (см. рис. 3.28), то, представив его рядом Фурье
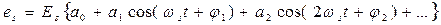 .
.
предыдущее выражение для выходного напряжения измерительной схемы
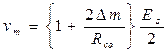
можно преобразовать к виду
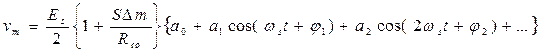
Для общего случая измеряемой величины, описываемой сигналом сложной формы, 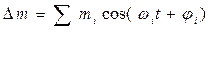 , имеем
, имеем
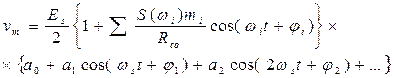
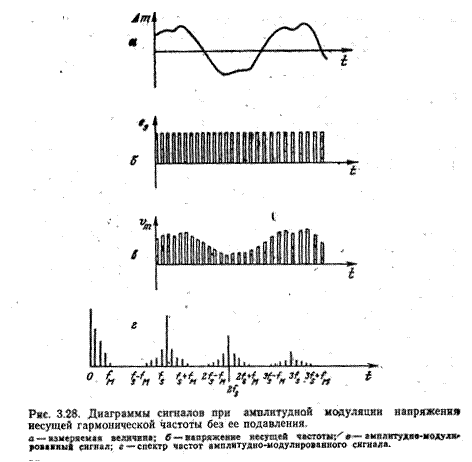
Иначе говоря, vm есть сумма модулированных по амплитудам членов разложения еs в ряд Фурье, и спектр напряжения vm (рис. 3.28, г) включает в себя спектр 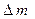 , который простирается до fм - верхней граничной частоты измеряемой величины (
, который простирается до fм - верхней граничной частоты измеряемой величины ( 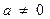 ), набор несущих частот nfs, (n=1, 2, ...), для которых
), набор несущих частот nfs, (n=1, 2, ...), для которых 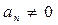 , нижнюю боковую полосу частот до nfs - fм и верхнюю боковую полосу частот до nfs + fм.
, нижнюю боковую полосу частот до nfs - fм и верхнюю боковую полосу частот до nfs + fм.
Чтобы иметь возможность выделить частоты спектра собственно измеряемой величины, нет нужды восстанавливать боковые полосы несущих частот, т. е.
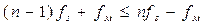
откуда 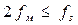 .
.
Таким образом, основная частота (частота первой гармоники) питающего напряжения должна по меньшей мере вдвое
превосходить верхнюю граничную частоту спектра измеряемой величины.
Модуляция по амплитуде с подавлением несущей. Когда используют мостовую или потенциометрическую схему с симметричным питанием, спектр выходного напряжения этих схем не содержит частотных составляющих питающего напряжения.
Например, для дифференциальной схемы с резистивными датчиками имеем 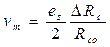
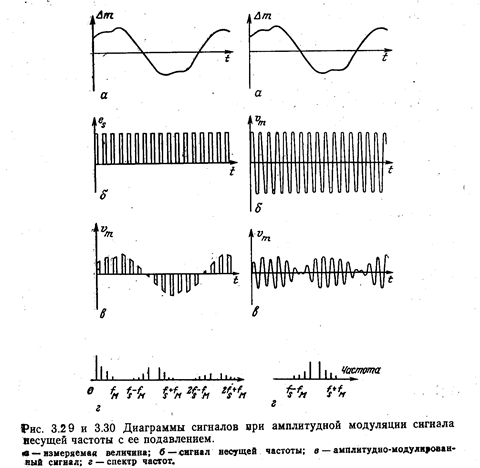
В общем случае (см. рис. 3.29), когда измеряемая величина и питающее напряжение измерительной схемы описываются сложными периодическими функциями, легко установить, что спектр выходного напряжения vm образован из спектра измеряемой величины с верхней граничной частотой fм (при условии, что 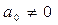 ), нижней боковой полосы частот до nfs – fм и верхней боковой полосы частот до nfs+fм, за исключением несущих частот nfs.
), нижней боковой полосы частот до nfs – fм и верхней боковой полосы частот до nfs+fм, за исключением несущих частот nfs.
Возможность выделить спектр измеряемой величины обеспечивается, как и в предыдущем случае, при выполнении условия 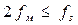
В частном случае питающего напряжения синусоидальной формы (рис. 3.30) частотный спектр vm составляет от . fs – fм до fs+fм , но без частоты fs. В отличие от модуляции по амплитуде с сохранением несущей, при подавлении последней пиковые значения vm не следуют за изменением 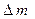 .
.
Дата добавления: 2016-06-18; просмотров: 2080;











