Торричелли, Паскаль, Бойль
Копатели колодцев во Флоренции знали, что есть предельная высота (ок. 10 м), выше которой отсасывающий насос не поднимает воду. Галилей и др. считали, что на этой высоте природа перестает бояться пустоты. Торричелли первым предположил, что дело тут в давлении воздуха, и в 1640-х гг. поставил свои опыты со столбом ртути. Еще он занимался гидравликой, оптикой, движением брошенных тел, геометрией и зачатками матана. Паскаль понял, что гипотезу Торричелли можно проверить, поднявшись в горы, и проверил ее в экспедициях 1648-1651 гг., после чего заключил, что «боязни пустоты» нет вообще, есть лишь давление воздуха. Этот вывод в работе 1660 г. подтвердил Бойль, откачивавший вакуумным насосом (усовершенствованным его учеником Гуком) воздух из сосуда и наблюдавшим, как меняется высота столбика ртути. Также он установил для воздуха закон РV = соnst (Вайнберг не указывает, учитывал ли он в каком-то виде температуру), и что воздух необходим для горения, поддержания жизни и распространения звука. Как уже говорилось выше, в этих опытах Вайнберг видит новый подход к исследованию природы: не довольствоваться наблюдением и воспроизведением встречающихся в жизни ситуаций, а смело ставить природу в сколь угодно искусственные условия.
Ньютон
Ньютон родился в 1642 г. Как замечает Вайнберг, человек, совершивший великие открытия и давший нам поныне действующий образец того, какой должна быть научная теория, был «странным типом». Каталог рукописей Ньютона, выставленных в 1936 г. на продажу на аукционе «Сотби», насчитывал 650 тыс. слов текстов об алхимии и 1.3 млн. – о религии. Еще Ньютон никогда не покидал родного маленького района Англии, даже не видел моря.
В 19 лет Ньютон поступил в Тринити-колледж Кембриджа, где был студентом-сайзером – т.е. не платил за обучение, проживание и питание, но был мальчиком на побегушках, в т.ч. у тех студентов, которые оплачивали свои счета. В 1665 г., спасаясь от чумы, Ньютон уезжает на семейную ферму, где проводит два года в самых продуктивных, по его собственному признанию, за всю его жизнь научных исследованиях. В 1667 г. Ньютон возвращается в Кембридж, а с 1669 г. занимает должность Лукасовского профессора математики, учрежденную в 1663 г. меценатом Г. Лукасом.
В 1672 г. Ньютон избран членом, а позже президентом Лондонского королевского общества. Само общество было основано в 1660 г. Несколько лондонцев, в том числе Бойль и Гук, создали его, чтобы обсуждать натурфилософию и наблюдать за экспериментами. Единственным иностранцем в нем в ту пору был голландец Гюйгенс. В 1662 г. общество получило королевскую грамоту и стало называться Лондонским королевским.
В 1675 г. Ньютон столкнулся с трудностью. После восьми лет членства в братстве Тринити-колледжа он должен был принять духовный сан в англиканской церкви, а для этого поклясться в вере в Святую Троицу, что для отрицавшего троичность Бога Ньютона было невозможно. К счастью, Г. Лукас, учредивший в свое время занимаемую Ньютоном должность, специально оговорил, что на ней не обязательно заниматься церковными делами. На этом основании король выпустил специальный указ, что на этой должности не обязательно иметь сан.
Впечатляющие открытия Ньютон сделал в оптике. С античности было известно, что проходящий через искривленное стекло белый свет становится разноцветным. Считалось, однако, что стекло окрашивает свет, как художник окрашивает белый лист, идея, что сам свет состоит из разноцветных компонентов, никому не приходила в голову. Ньютон, поставив в 1665 г. ряд опытов с призмами, заключил, что: а) белый свет – смесь разноцветных компонентов и б) угол преломления зависит от цвета. Он проверил также, что синий или красный свет дальше уже не расщепляется и что полученное призмой многоцветье можно собрать обратно в белый свет. В 1669 г. Ньютон изобрел телескоп-рефлектор, почти свободный от хроматической аберрации (песню портила линза в окуляре). Телескоп длиной всего 15 см давал увеличение в 40 раз. В лекции 1675 г. Ньютон провозглашает корпускулярную теорию света (систематически он изложит ее в книге «Оптика», написанной в начале 1690-х и опубликованной в 1704 г.).
На Ньютона накинулся Гук (сторонник гюйгенсовой волновой теории света). Он заявил, что а) сам проводил те же опыты с призмами и б) они не доказывают, что призма расщепляет белый свет, а не раскрашивает его. Но сейчас мы знаем, кто был прав, нес па?
К 1665 г. относятся первые результаты Ньютона по бесконечно малым. Он положил, что если известна зависимость расстояния от времени 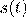 , то скорость в момент
, то скорость в момент  равна
равна 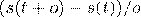 , где
, где  – бесконечно малая величина (флюксия). Раскрывая скобки и пренебрегая членами, пропорциональными
– бесконечно малая величина (флюксия). Раскрывая скобки и пренебрегая членами, пропорциональными 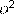 и выше (Вайнберг не указывает, рассматривал ли Ньютон случай, когда
и выше (Вайнберг не указывает, рассматривал ли Ньютон случай, когда 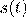 – не полином), получаем то, что сейчас называется производной. Также Ньютон изобрел интегрирование и рассматривал суммы бесконечных рядов. В общем, сейчас считается, что Ньютон открыл матан на десятилетие раньше Лейбница, но переоткрывший его независимо Лейбниц раньше опубликовал результаты.
– не полином), получаем то, что сейчас называется производной. Также Ньютон изобрел интегрирование и рассматривал суммы бесконечных рядов. В общем, сейчас считается, что Ньютон открыл матан на десятилетие раньше Лейбница, но переоткрывший его независимо Лейбниц раньше опубликовал результаты.
У самого знаменитого открытия Ньютона – закона всемирного тяготения – были, конечно, предвестники. Идея, что сила тяжести ослабевает при удалении от Земли, высказывалась еще в IХ в. ирландским монахом Д. Скотом, но с движением планет он ее не связывал. Идея, что сила, удерживающая планеты на орбитах (без упоминания, что это сила тяжести) ослабевает как 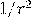 , высказывалась в 1645 г. И. Буйо, на коего ссылается Ньютон. Связь закона обратных квадратов с третьим законом Кеплера, кроме Ньютона, видели Гук, Галлей и Рен. В 1659 г. Гюйгенс вычислил, что центробежная сила пропорциональна
, высказывалась в 1645 г. И. Буйо, на коего ссылается Ньютон. Связь закона обратных квадратов с третьим законом Кеплера, кроме Ньютона, видели Гук, Галлей и Рен. В 1659 г. Гюйгенс вычислил, что центробежная сила пропорциональна 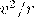 – о чем Ньютон, возможно, не знал, во всяком случае он утверждал, что получил этот результат в 1666 г., тогда же, когда отождествил силу, искривляющую планетные орбиты, с силой тяжести, и вывел из третьего закона Кеплера закон обратных квадратов. В этом ему помог радиус орбиты Луны, хорошо известный по суточным параллаксам. Ньютон понял, что центростремительное ускорение Луны меньше ускорения свободного падения на Земле так, как если бы оно ослабевало с удалением от центра Земли как
– о чем Ньютон, возможно, не знал, во всяком случае он утверждал, что получил этот результат в 1666 г., тогда же, когда отождествил силу, искривляющую планетные орбиты, с силой тяжести, и вывел из третьего закона Кеплера закон обратных квадратов. В этом ему помог радиус орбиты Луны, хорошо известный по суточным параллаксам. Ньютон понял, что центростремительное ускорение Луны меньше ускорения свободного падения на Земле так, как если бы оно ослабевало с удалением от центра Земли как 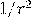 .
.
Тогда Ньютон еще не пришел к идее, что сила тяготения пропорциональна массе, и его беспокоило, почему третий закон Кеплера не зависит от размеров планеты. Кроме того, он вывел из третьего закона Кеплера, что 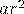 , где
, где  – центростремительное ускорение,
– центростремительное ускорение,  – расстояние до Солнца, одинаково для всех планет, но почему оно совсем другое для Луны, если
– расстояние до Солнца, одинаково для всех планет, но почему оно совсем другое для Луны, если  – расстояние от Луны до Земли? Также ему было непонятно, почему надо брать расстояние именно до центра Земли. Наконец, в своей работе он принял движение планет равномерным по окружности, что противоречило первым двум законам Кеплера.
– расстояние от Луны до Земли? Также ему было непонятно, почему надо брать расстояние именно до центра Земли. Наконец, в своей работе он принял движение планет равномерным по окружности, что противоречило первым двум законам Кеплера.
Пока Ньютон, ничего не публикуя, латал эти прорехи, Гук в 1679 г. опубликовал свои «кутлеровские лекции», в которых заявил, что:
1) сила тяжести действует и на небесные тела
2) тело, «принужденное» двигаться прямолинейно и равномерно, а потом предоставленное само себе, продолжает такое движение так что, чтобы искривлять орбиты, нужна сила. В приводимой Вайнбергом цитате не утверждается прямо, что это сила тяжести, но легко сложить два и два. Первый закон Ньютона, который здесь предвосхищает Гук, на самом деле сильнее: тело начнет двигаться прямолинейно и равномерно, как только будет предоставлено само себе, независимо от того, как оно двигалось раньше. Из приводимой Вайнбергом цитаты не очевидно, и Вайнберг не указывает, понимал ли это Гук – Авт.
3. Сила притяжения убывает с расстоянием. В письме Ньютону Гук уточнил: по закону обратных квадратов.
В 1687 г. выходят «Математические начала натуральной философии». Книга не содержит формул, зачатки матана выражены в ней на геометрическом языке. В общем, она и построена в стиле «Начал» Евклида. Сначала идут восемь определений. Определяются следующие понятия: масса, количество движения (импульс), «врожденная сила материи», которая есть «присущая ей сила сопротивления, по которой всякое отдельное тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения» и «приложенная сила», а также центростремительное ускорение и его свойства.
Массу Ньютон определяет как произведение плотности на объем. Плотность он не определяет, но ею пользовался (и отмечал ее связь с удельным весом) еще Архимед, и, как отмечает Вайнберг, интуитивно понятно, что она определяется веществом. Ньютон отмечает, что масса связана с весом, но не смешивает эти понятия. Количество движения он определяет как произведение массы на скорость. Про «врожденную силу материи» он говорит, что она пропорциональна массе. «Приложенную силу» он определяет так: «Приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения». Это определение выглядит «философски» в том смысле, что не указано ни как измерить, ни как вычислить силу.
Давать определение пространству и времени Ньютон отказывается, но описывает их такими словами:
«I. Абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно, и иначе называется длительностью...
Относительное, кажущееся или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения, мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как то: час, день, месяц, год.
II. Абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остаётся всегда одинаковым и неподвижным. Относительное есть его мера или какая-либо ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которая в обыденной жизни принимается за пространство неподвижное: так, например, протяжение пространств подземного воздуха или надземного, определяемых по их положению относительно Земли».
Я привел чуть более полную цитату, чем у Вайнберга – Авт.
Лейбниц и Беркли критиковали определения Ньютона, указывая, что мы можем определить положение в пространстве только относительно какого-либо тела, а во времени – только относительно какого-либо события, а раз так, введенные Ньютоном понятия абсолютного пространства и времени бесполезны или даже бессмысленны. Ньютон признает, что обычно мы имеем дело с относительными перемещениями и скоростями, но заявляет, что ускорение не относительно, а раз так, то можно говорить об абсолютном пространстве.
Далее он формулирует три знаменитых закона.
Первый закон
«Всякое тело продолжает удерживаться в состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».
Сейчас он начинается со слов «существуют такие системы отсчета, что…», но Ньютон, видимо, рассматривал движение в своем абсолютном пространстве и о системах отсчета не думал. Между тем тогда получается, что первый закон есть тривиальное следствие второго, тогда как в современной формулировке это не так: первый закон утверждает существование систем отсчета, в которых выполняется второй. Возможно, Ньютон решил выделить его в отдельный закон за контринтуитивность и опровержение веками господствовавшего мнения Аристотеля, что движение возможно только под действием силы. – Авт.
Вайнберг отмечает, что первый закон был известен и до Ньютона – например, Гассенди, Гюйгенсу и Декарту, о чем-то подобном, как мы видели выше, писал Гук.
Второй закон
«Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует».
В этой формулировке есть проблема: на самом деле приложенной силе пропорциональна скорость изменения импульса. Вайнберг отмечает это, но не говорит, стукнулся ли об это кто-нибудь лбом, и прежде всего сам Ньютон. Впрочем, учитывая, сколько вещей в тех же «Математических началах» успешно рассчитал Ньютон, вероятно, в расчетах он пользовался правильным соотношением.
Третий закон
«Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны»
Сформулировав три закона, Ньютон переходит к следствиям из них, самым важным из которых оказывается закон сохранения импульса. Затем Ньютон переходит к выводам (т.е. приложениям своих законов к разным задачам). Так, он показывает, как из действия центральной силы с законом обратных квадратов следуют законы Кеплера (Вайнберг отмечает, что второй и третий законы Кеплера не были тогда общеприняты, и именно авторитет Ньютона сделал им репутацию).
В той же книге I он объявляет, что отказывается от идеи отношения бесконечно малых величин в пользу предела отношения. «Предельные отношения исчезающих количеств не суть отношения пределов этих количеств, а суть те пределы, к которым при бесконечном убывании количеств приближаются отношения их и к которым эти отношения могут подойти ближе, нежели на любую наперед заданную разность, но которых превзойти или достигнуть на самом деле не могут, ранее чем эти количества уменьшатся бесконечно». Снова привожу чуть более полную цитату, чем Вайнберг – Авт. Вайнберг отмечает, что это, в сущности, современная идея предела. Что не отменяет необходимости ее подкрутить, ибо, например, «достигнуть не могут» неверно для производной от константы – Авт.
В Книге II Ньютон занимается движением тел в жидкости, звуком и расчетом скорости океанских волн.
Книга III посвящена астрономии. Ньютон обосновывает законы Кеплера, ссылаясь на движение планет, Луны, спутников Юпитера и Сатурна и наблюдавшейся самим Ньютоном кометы 1680 г. Также он указывает, что наблюдаемые фазы всех пяти известных тогда планет говорят об их обращении вокруг Солнца. Здесь он формулирует закон всемирного тяготения, хотя и не в виде формулы. Кстати говоря, Ньютон не исключал, что между мельчайшими частицами вещества есть силы притяжения, иные, чем известные ему три (гравитация, электростатическая и магнитная), но слишком короткодействующие и потому неизвестные человечеству (с. 296). Все-таки он был гениален.
В 1791-1798 гг. Кавендиш лабораторно измерил силу притяжения между телами. Вместо публикации абсолютного значения G он, однако, заключил, что средняя плотность Земли равна 5.48 плотности воды (для чего использовал известный объем Земли и ускорение свободного падения). Вайнберг отмечает, что публикация пропорций вместо абсолютных значений была традицией эпохи, и связывает это, как минимум, с тем, что не существовало международных единиц длины и массы (первой такой системой стала метрическая, которая постепенно принималась разными странами начиная с 1799 г.).
Используя свой закон, Ньютон вывел соотношение масс Юпитера, Сатурна и Солнца (и Земли, хотя тут он ошибся в два раза). По Вайнбергу, Ньютон вполне понимал, что неточности в наблюдениях ведут к ошибкам в результате, но не придавал этому значения и все еще выписывал абсурдно много значащих цифр. Первые измерения размеров Солнечной системы с реалистичными результатами провели Рише и Кассини в 1672 г. Они измерили расстояние до Марса, наблюдая его из разных точек, а т.к. отношения размеров орбит были известны, они получили и расстояние от Солнца до Земли. Мимо современного значения они промахнулись только на 6%. Еще более точные измерения были выполнены во время прохождения Венеры по диску Солнца в 1761 и 1769 гг.
Также Ньютон предсказывает, что ускорение свободного падения будет зависеть от широты (это подтвердили опыты 1740х гг. с маятниками); объясняет прецессию земной оси (известную древним астрономам как прецессия равноденствия) и измеренную аз-Заркали прецессию орбиты Земли. Там, где Ньютон делал количественные расчеты, их результаты совпадали с наблюдениями, но установлено, что кое-где он их просто подгонял. Ньютон дал также качественное объяснение приливам и отливам, хотя, конечно, рассчитать их высоту не мог (она сильно зависит от географии). Природу тяготения он обсуждать отказывается, говоря, что не смог вывести ее из явлений, и произнеся свое знаменитое «гипотез не измышляю».
Хотя в Англии Ньютон был знаменит и удостоен многих почестей, его теория подвергалась и критике. Часть критики была идеологической – так, епископ Беркли ругал теории Ньютона за то, что они оставляли мало места для Творца (это Ньютона-то, который приписывал свечение Солнца и звезд, а также стабильность Солнечной системы, напрямую Господней воле). Некоторые деятели все еще понимали физику как философские рассуждения о «природе» и «сущностях» – так, Н. Мальбранш назвал «Начала» работой геометра, а не физика. Ну и где теперь Н. Мальбранш? Последователи Декарта и Лейбница утверждали, что столь странную гипотезу, как сила тяготения, действующая через огромные пространства пустоты, нельзя принимать, пока этому тяготению не найдено объяснения. Были возражения и по существу. Так, Гюйгенс сомневался, что сила притяжения пропорциональна массе. Похоже, он был введен в заблуждение ошибками в экспериментах с маятниками и широтой, из которых, казалось, следовало, что Земля не сплющена с полюсов.
Однако появлялись новые свидетельства в пользу теории Ньютона. Галлей, сведя воедино результаты наблюдений комет в 1531, 1607 и 1682 гг., показал, что это одна комета. В 1758 г. Клеро с соратниками предсказали ее возращение в перигелий в середине апреля 1759 г., для чего им пришлось учесть притяжение Юпитера и Сатурна (зато ошиблись всего на месяц). В 1749 г. д’Аламбер опубликовал точные и правильные (в отличие от расчетов самого Ньютона) расчеты прецессии земной оси.
Вайнберг проводит аналогию между критикой теории тяготения последователями Декарта и Лейбница и критикой квантовой механики Эйнштейном и др. И выводит простую мораль: успешно работающая теория не может быть просто ошибочна. Она может лишь быть уточнена и включена в более глубокую теорию.
Дата добавления: 2016-07-22; просмотров: 2272;











