РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Сложными называются разветвленные электрические цепи с несколькими источниками питания.
Универсальным методом анализа и расчета сложных цепей является метод непосредственного применения первого и второго законов Кирхгофа соответственно для узловых точек и замкнутых контуров.
Однако при значительном числе ветвей и узловых точек использование этого метода усложняется необходимостью совместного решения большого числа уравнений. В этих и некоторых других случаях может оказаться целесообразным применение иных методов расчета, основанных на тех же законах Кирхгофа. В зависимости от конфигурации расчетной схемы и поставленной задачи следует применять тот метод расчета, который в данном случае является наиболее эффективным.
Непосредственное применение законов Кирхгофа для расчета сложных цепей. Все э.д.с., токи и сопротивления любой цепи связаны между собой уравнениями, выражающими законы Кирхгофа. Эти уравнения могут быть записаны, если известны не только величины э.д.с. и токов, но и их направления.
Если известными являются величины э.д.с. и их направления, а так же величины сопротивлений сложной цепи, то, применяя законы Кирхгофа, можно составить столько независимых уравнений, сколько различных неизвестных токов имеется в этой цепи. Однако для составления этих уравнений необходимо предварительно задаться произвольными направлениями неизвестных токов, которые принято считать положительными.
Если в результате решения составленной системы уравнений найденная величина тока имеет знак «плюс», то это означает, что его направление совпадает с ранее выбранным положительным направлением. В противном случае фактическое направление тока противоположно выбранному положительному направлению.
Для получения требуемого числа независимых уравнений следует применить первый закон Кирхгофа ко всем узловым точкам, кроме одной, т. е. составить (n—1) уравнений, если число узлов равно п. Недостающие уравнения должны быть составлены по второму закону Кирхгофа так, чтобы каждое следующее уравнение не могло быть получено из предыдущих.
Расчет сложной цепи при помощи уравнений Кирхгофа проводят в следующей последовательности:
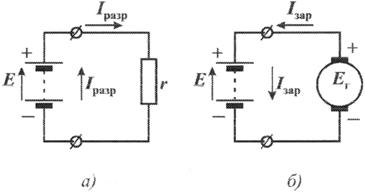
Рис. 1.11. Схема разряда (а) и заряда (б) аккумулятора
1) по возможности упрощают расчетную схему (заменив, например, несколько параллельно соединенных сопротивлений одним эквивалентным сопротивлением);
2) наносят на схеме известные направления э.д.с.;
3) задаются произвольными положительными направлениями токов;
4) составляют уравнения по первому закону Кирхгофа для всех узловых точек схемы, кроме одной;
5) составляют недостающие уравнения по второму закону Кирхгофа, обходя замкнутые контуры по часовой стрелке или против часовой стрелки. При этом э.д.с. и токи, совпадающие с направлением обхода, принимаются положительными, а э.д.с. с. и токи, противоположные (т. е. встречные) этому направлению, — отрицательными;
6) решают составленную систему уравнений и определяют неизвестные токи. Если некоторые значения токов получаются со знаком «минус», то это означает, что они имеют направления, обратные тем, которые были условно приняты для этих токов в начале расчета.
Необходимо отметить следующее: если в результате расчета сложной цепи фактическое направление тока в энергопреобразующем устройстве (электрической машине или аккумуляторе) совпадает с направлением его э.д.с., то это свидетельствует о том, что рассматриваемое устройство работает в качестве источника электроэнергии, а не электроприемника. Если направление тока обратно направлению э.д.с., то это означает, что устройство является электроприемником. Для пояснения сказанного на рис. 1.11 приведена схема разряда (а) и заряда (б) аккумулятора. В схеме (а) аккумулятор работает как генератор, в схеме (б) он является потребителем электрической энергии.
В отдельных случаях могут быть заданы лишь некоторые значений э.д.с., токов и сопротивлений. Общее число неизвестных величин должно соответствовать возможному числу независимых уравнений, составляемых по законам Кирхгофа для рассматриваемой схемы. В таких случаях приходится в начале расчета задаваться положительными направлениями не только неизвестных токов, но и неизвестных э.д.с. (или напряжений).
Фактические направления этих э.д.с, напряжений и токов находятся в зависимости от полученного знака ( + или —) у каждой из величин, найденных в результате решения составленной системы уравнений.
Пример 1.2. Найти токораспределение в схеме, изображенной на рис. 1.12,а. Исходные данные: Е1=72 в, Е2 = 48 в, r1 = 3 ом, r2-4 ом, r3 = 6 ом, r4 = 1О ом, r5= 15 ом.
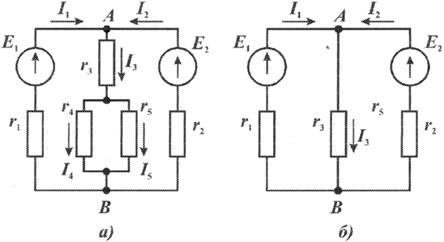
Рис. 1.12. Расчетные схемы к примеру 1.2:
а—исходная; б—упрощенная
Решение. Предварительно упрощаем схему и находим эквивалентное сопротивление, заменяющее сопротивления: r3, r4, r5:
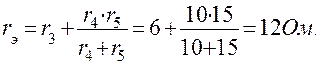
На упрощенной схеме (рис. 12. б) наносим заданные положительные направления э.д.с., E1 и Е2 и произвольно намечаем направления неизвестных токов I1 I2 и I3 . Применяя к этой схеме законы Кирхгофа, составляем три уравнения:
| I1 + I2 = I3 E1 – E2 = I1 r1 – I2 r2 E1 = I1 r1 + I3 r3 | I1 + I2 = I3 72 – 48 = 3 I1 – 4I2 72 = 3I1 + 12 I3 |
Решая эту систему уравнений, находим:
I1 = 6A; I2 = -1,5A; I3 = 4,5a
Полученный отрицательный знак у величины тока I2 означает, что в действительности этот ток направлен в противоположную сторону. Ток I3 распределяется между параллельными ветвями r4 и r5 обратно пропорционально этим сопротивлениям.
Пример 1.3. Найти токораспределение в схеме, изображенной на рис. 1.13. Исходные данные: Е1 = 10 В, Е2 = 10 В, Е3= 11О В, Е4 = 120 B, r1 = 5 Ом,. r2 = 3 Ом, r3 = 8 Ом, r4 = 4 Ом, r5 = 3 Ом, r6 = 4 Ом, r7 = 5 Ом, r8 = 6 Ом.
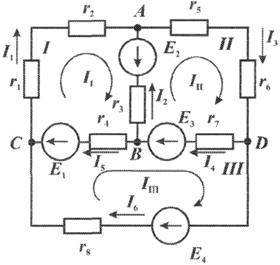
Рис. 1.13. Схема цепи к расчету методом контурных токов
Решение. Подставив в уравнения (1.23) известные значения э.д.с. и сопротивлений цепи и решая совместно эти уравнения, находим
II = 5A, III = 8A, IIII = 4A
Значения действительных токов в рассматриваемой цепи:
II = II = 5A, I2 = III – II = 8 – 5 = 3A, I3 = III = 8a
I4 = III – IIII = 8 – 4 = 4A, I5 = II – IIII = 5 – 4 = 1a, I6 = IIII = 4A
Рис. 1.14. Схема цепи расчету методом узлового напряжения
Метод узлового напряжения. Рассматриваемый метод расчета целесообразно применять к схеме (рис. 1.14), имеющей несколько параллельных ветвей, сходящихся в двух узловых точках, а также к, электрическим цепям, которые в результате несложных преображений могут быть приведены к схеме с двумя узлами.
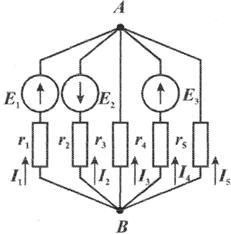
Рис. 1.14 Схема цепи к расчету методом узлового напряжения.
Примем направления токов во всех ветвях одинаковыми — от узла В к узлу А. Напряжение UAB между точками А и В назовем узловым напряжением.
Применим к ветви с э.д.с. Е1 второй закон Кирхгофа:
E1 = UAB + I1 r1,
откуда
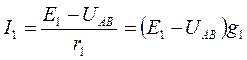 (а)
(а)
Аналогичным путем получим:
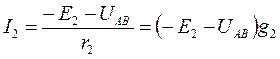 (б)
(б)
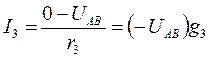 (в)
(в)
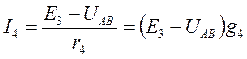 (г)
(г)
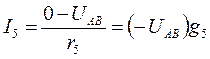 (д)
(д)
По первому закону Кирхгофа
I1 + I2 + I3 + I4 + I5 = 0
или
(E1 – UAB) g1 + (-E2 – UAB) g2 – UAB g3 + (E3 – UAB) g4 – UAB g5 = 0
Отсюда получаем формулу для определения узлового напряжения:
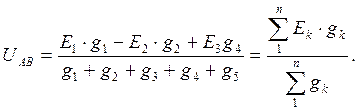 (1.24)
(1.24)
Произведение Ekgk для k-й ветви следует брать со знаком минус, если направление э.д.с. Ek противоположно принятому направлению тока (например, для второй ветви, рис. 1.14).
Определив узловое напряжение UAB по формуле (1.24), нетрудно найти значения токов в отдельных ветвях схемы по формулам (а) - (д).
Пример 1.4. Найти токораспределение в схеме, представленной на рис. 1.14, Исходные данные: E1 =60 В, Е2 = 50 В, E4 = 100 В, r1=5 Ом, r2 = 25 Ом, r3 = 50 Ом, r4 = 10 Ом, r5 = 25 Ом.
Решение. Узловое напряжение
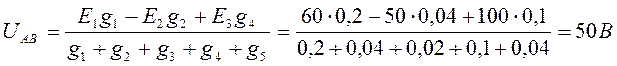
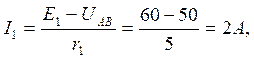
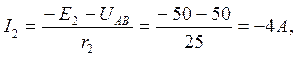
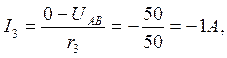
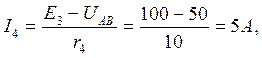
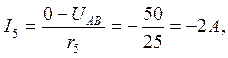
Проверка:
I1 + I2 + I3 + I4 + I5= 2 –4 –1 + 5 – 2 = 0
Дата добавления: 2020-10-14; просмотров: 653;











