РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ

Соединения источников и потребителей электроэнергии. В рассмотренной ранее простейшей электрической цепи (см. рис. 1.3) генератор, электроприемник и связывающие их провода, по которым электрическая энергия передается от генератора к приемнику, соединены между собой последовательно. Этот способ соединения применяется для того, чтобы связать в общую электрическую систему разнохарактерные с энергетической точки зрения элементы цепи генераторы, электроприемники и линии передачи электрической энергии. Однородные в энергетическом отношении элементы системы, например генераторы или электроприемники, как правило, соединяются между собой параллельно. При таком способе соединения достигается относительная независимость в управлении и работе отдельных источников и потребителей электроэнергии. Между тем при последовательном соединении практически невозможно включать и отключать отдельно каждый генератор или электроприемник, а также устанавливать для любого из них требуемый режим, работы. Кроме того, при последовательном соединении приемников, например электрических ламп, перегорание одной из них влечет за собой погасание всех остальных.

Совместная параллельная работа генераторов на общую электрическую нагрузку имеет значительные преимущества в сравнении с раздельной работой каждого генератора на свою нагрузку. Во-первых, повышается надежность питания потребителей, так как в случае аварийного отключения одного из генераторов оставшиеся в работе генераторы могут обеспечить бесперебойное электроснабжение наиболее ответственных нагрузок. Во-вторых, при параллельной работе можно в случае снижения нагрузки (например, в ночное время или в выходные дни) отключать часть генераторов, что повышает экономичность эксплуатации энергетических установок.

В тех случаях, когда один источник (например, электрохимический аккумулятор с э.д.с. Е = 1,25—2,4 В) не обеспечивает требуемого напряжения (110 или 220 В), приходится применять последовательное соединение однотипных источников.

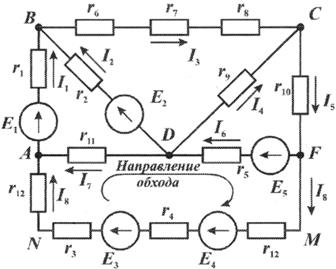
Рис. 1.6 Схема сложной цепи постоянного тока

Последовательное включение однотипных приемников (например, электрических ламп) применяется в исключительных случаях, когда напряжение источника значительно превышает номинальное напряжение отдельных электроприемников.

Законы Кирхгофа. При анализе и расчете электрических цепей, образуемых путем последовательного и параллельного соединения источников и потребителей электроэнергии, составляют электрическую схему, на которой показывают, как осуществляются эти соединения (рис 1.6).

Несколько последовательно соединенных элементов, по которым проходит один и тот же ток, образуют ветвь. В частном случае в ветви может быть лишь один элемент. Некоторые ветви (например, АВ, ANMF) содержат как сопротивления r, так и э.д.с. Е. Другие ветви (например, AD, DC, BC) имеют только сопротивления r.

Место соединения трех или более ветвей называют узловой точкой, или узлом. Так, например, в узловой точке А сходятся три ветви: АВ, АD и ANMF.

Ряд ветвей, образующих замкнутую электрическую цепь, называют контуром (например, ABDA, ADFMNA).

К узловым точкам схемы применим первый закон Кирхгофа, а к контурам — второй закон Кирхгофа.

Согласно первому закону Кирхгофа, сумма токов, притекающих к любой точке разветвления (узловой точке), равна сумме токов, уходящих от нее. Если токи, притекающие к точке разветвления, считать положительными, а уходящие от нее, — отрицательными, то первый закон Кирхгофа можно сформулировать так: алгебраическая сумма токов в узловой точке равна нулю:

SI = 0 (1.10)

В качестве примера напишем уравнение первого закона Кирхгофа для узловой точки А электрической схемы, представленной на рис. 1.6:

I₇ + I₈ = I₁

I₇ + I₈ – I₁ = 0

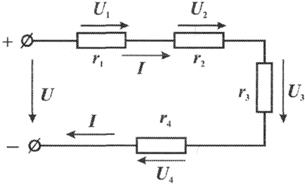
Рис. 1.7 Цепь с последовательным соединением сопротивлений

Согласно второму закону Кирхгофа, во всяком замкнутом контуре алгебраическая сумма э.д.с. равна алгебраической сумме падений напряжения на всех сопротивлениях, входящих в этот контур:

S E = SIr (1.11)

При обходе замкнутого контура по часовой стрелке (или против часовой стрелки) э.д.с. и токи, направления которых совпадают с принятым направлением обхода, следует считать положительными, а э.д.с. и токи, направленные встречно, — отрицательными.

Для примера рассмотрим замкнутый контур ADFMNA (рис. 1.6). При указанных на рисунке направлениях токов и э.д.с. и принятом обходе этого контура по часовой стрелке уравнение второго закона Кирхгофа принимает следующий вид:

-E₅ + E₄ + E₃ = -I₇ r₁₁ – I₆ r₅ + I₈ (r₁₃ + r₄ + r₃ +r₁₂)

В некоторых расчетах оказывается более удобным пользоваться уравнением второго закона Кирхгофа, записанным как

S E = S U + SIr (1.12)

Здесь часть слагаемых Ir, относящаяся к определенным участкам контура, заменена напряжениями U на этих участках.

Цепи с последовательным соединением. Если электрическая цепь состоит из нескольких последовательно соединенных участков с сопротивлениями r₁, r₂, r₃, r₄ (рис. 1.7), то через все участки протекает один и тот же ток I.

При отсутствии на участках цепи собственных э.д.с.[4] общее напряжение U, приложенное к зажимам всей цепи, равно сумме падений напряжения на отдельных элементах цепи (второй закон Кирхгофа):

U + U₁ + U₂ + U₃ + U₄ (1.13)

или

U = I r₁ + I r₂ + I r₃ + I r₄ = I (r₁ + r₂ + r₃ + r₄) (1.14)

Из этого выражения следует, что общее сопротивление r равно сумме сопротивлений всех последовательно соединенных элементов цепи, а напряжения между элементами распределяются прямо пропорционально их сопротивлениям.

Если уравнение (1.14) умножить на I, то получим

U = I² r₁ + I² r₂ + I² r₃ + I² r₄ (1.15)

или

P = P₁ + P₂ + P₃ + P₄ (1.16)

т. е. общая мощность Р, потребляемая цепью, равна сумме мощностей, потребляемых отдельными ее элементами.

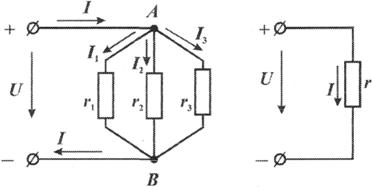
Рис. 1.8 Разветвленная цепь постоянного тока

Цепи с параллельным соединением. При параллельном соединении электроприемников (рис. 1.8) все они находятся под одинаковым напряжением U.

Обозначим сопротивления отдельных электроприемников через r₁, r₂, r₃, их проводимости - соответственно через g₁, g₂, g₃, а токи—через I₁, I₂, I₃.

Общий ток I в неразветвленной части цепи равен сумме токов, потребляемых отдельными электроприемниками:

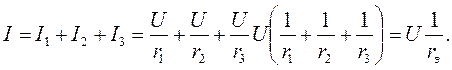(1.17)

или

I = U g₁ + U g₂ + U g₃ = U (g₁ + g₂ + g₃) = U g_э (1.18)

Эквивалентная проводимость разветвленной цепи равна сумме проводимостей отдельных ее ветвей:

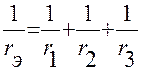(1.19)

или

g = g₁ + g₂ + g₃ (1.9а)

В частном случае, когда цепь содержит два параллельно включенных сопротивления r₁ и r₂, эквивалентное сопротивление r_э удобно определять по формуле, вытекающей из выражения (1.19):

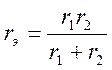(1.20)

Умножив уравнения (1.17) на U, получим

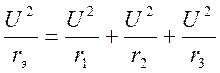(1.21)

или

P₁ = P₁ + P₂ + P₃ (1.22)

Из изложенного следует что мощность, расходуемая в разветвленной цепи, равна сумме мощностей, потребляемых отдельными приемниками или одним эквивалентным приемником. Проводимость эквивалентного приемника равна сумме проводимостей всех параллельно включенных электроприемников. Токи в этих приемниках так же, как и мощности, распределяются всегда пропорционально проводимостям.

При включении нескольких генераторов для совместной параллельной работы (рис. 1.9) они соединяются между собой одноименными зажимами, а к общим узловым точкам присоединяется внешняя цепь (нагрузка).

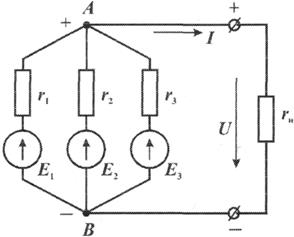
Рис. 1.9 Параллельна работа источника питания

При этом э.д.с. всех генераторов будут иметь одинаковое направление относительно их общей нагрузки.

Расчет смешанной цепи с одной э.д.с. Основная задача расчета электрических цепей — определить токи и мощности в различных элементах цепи (генераторах, электроприемниках и линиях, соединяющих источники энергии с потребителями), а также напряжения на отдельных элементах исследуемой цепи.

Исходными данными для расчета обычно являются заданные э.д.с., действующие в этой цепи, и характеристики (параметры) различных элементов цепи, т. е. либо их сопротивления, либо номинальные напряжения и мощности. При условии постоянства (по величине и направлению) действующих в цепи э.д.с. и неизменности сопротивлений, образующих эту цепь, картина распределения напряжений, токов и мощностей в данной схеме может быть только одна, т. е. задача имеет однозначное решение.

Если электрическая цепь представляет собой сочетание последовательно и параллельно включенных сопротивлений (смешанная схема соединений) и при этом имеет один источник питания (одну э.д.с.), то она рассчитывается в следующем порядке: 1) путем последовательного упрощения схемы находят общее сопротивление цепи; 2) по закону Ома определяют общий ток; 3) находят распределение токов и напряжений в схеме. Методику расчета подобных цепей поясним на числовом примере.

Пример 1.1. Рассмотрим цепь, изображенную на рис 1.10. Исходные данные:

U = 240 В, r₁ = 10 Ом, r₂ = 20 Ом, r₃ = 60 Ом, r₄ = 9 Ом, r₅ = 30 Ом, r₆ = 4 Ом, r₇ = 2 Ом.

Найти распределение токов в схеме.

Решение. Определяем эквивалентное сопротивление между точками А В:

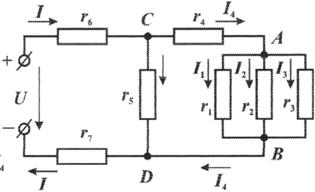
Рис. 1.10. Смешанная цепь постоянного тока

Складывая последовательно соединенные сопротивления r_АВ и r₄, получаем сопротивление

r¢ = r_AB + r₄ = 6 + 9 = 15 Ом

Сопротивление r' в свою очередь оказывается соединенным параллельно сопротивлением r₅:

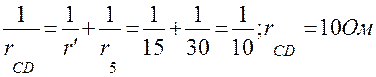
Общее сопротивление цепи

R = r₆ + r_CD + r₇ = 4 + 10 + 2 = 16 Ом

Общий ток

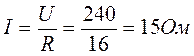
Напряжение между точками С и D

U_CD = I r_CD = 15 × 10 = 150 B

Токи в сопротивлениях r' и r₅:

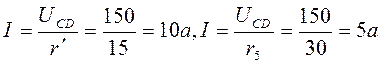
Напряжение между точками А и В

U_AB = I₄ r_AB = 10 × 6 = 60 B.

Токи в сопротивлениях r₁, r₂ и r₃:

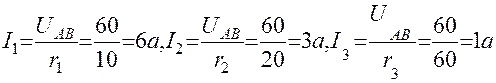
Во избежание встречающихся ошибочных представлений необходимо обратить внимание на следующее. В электрической цепи всегда устанавливается ток I такой величины, при которой приложенное к этой цепи напряжение U полностью уравновешивает (компенсирует) потери напряжения во всех последовательно включенных элементах цепи. Изменение величины сопротивления любого участка электрической схемы неизбежно влечет за собой изменение как общего тока, так и токов, протекающих в отдельных элементах этой схемы

Так, например, изменение величины или отключение сопротивления r₃ в схеме рис. 1.10 вызывает изменение величин всех токов.

Метод контурных токов. При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа и тем самым значительно сократить общее число совместно решаемых уравнений.

Сущность этого метода поясним на рис. 1.13, на котором представлена сложная цепь с узловыми точками А, В, С, D. Заданную схему разбиваем на три смежных контура /, //, /// с произвольно выбранными направлениями токов. Если считать, что в каждом из этих контуров протекает свой контурный ток (I_I, I_II, I_III), то в ветвях, являющихся общими для двух смежных контуров, протекающие токи равны алгебраической сумме двух контурных токов (в ветви АВ протечет ток I₂ = I_II - I_I, в ветви ВС - ток I₅ = I_I - I_III и в ветви DB - ток I₄ = I_II - I_III).

Применяя к отдельным контурам второй закон Кирхгофа, получим систему с числом уравнений, равным числу контурных токов[5]:

E₁ + E₂ = I₁ (r₁ + r₂) + (I_I – I_II) + (I_I – I_III) r₄

E₃ - E₂ = I_II (r₅ + r₆) + (I_II – I_III) r₇+ (I_II – I_I) r₃

E₄ – E₁ – E₃= I_III r₃ + (I_III – I_I) r₄+ (I_III – I_II) r₇

Эти уравнения можно представить в виде, более удобном для их совместного решения:

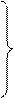E₁ + E₂ = I₁ (r₁ + r₂ + r₃ + r₄) – I_II r₃ – I_III r₄

E₃ - E₂ = I_II (r₅ + r₆ + r₇ + r₃) – I_I r₃ – I_III – r₇ (1.23)

E₄ – E₁ – E₃= I_III (r₄ + r₇ + r₈) - I_Ir₄ – I_II r₇

Определив контурные токи I_I, I_II, I_III, нетрудно найти токи в смежных ветвях АВ, ВС и DB.