Цепь переменного тока с активным сопротивлением и индуктивностью
Рис.2.21 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
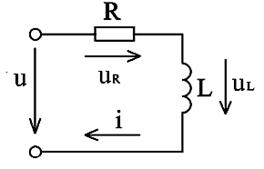
Рис.2.21. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть мгновенный ток в цепи изменяется по закону 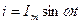 . Тогда мгновенное напряжение на активном сопротивлении
. Тогда мгновенное напряжение на активном сопротивлении 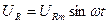 , так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности
, так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности 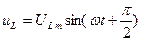 , поскольку на индуктивности напряжение опережает по фазе ток на угол
, поскольку на индуктивности напряжение опережает по фазе ток на угол 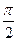 .
.
Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.22).
Векторы 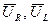 и
и 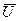 образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем
образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем 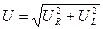 . Но
. Но 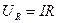 , а
, а 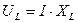 , где
, где 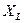 - индуктивное сопротивление, следовательно:
- индуктивное сопротивление, следовательно:
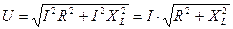 , откуда
, откуда
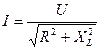 . (2.22)
. (2.22)
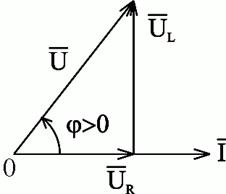
Рис.2.22. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью
Введем обозначение 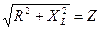 , где Z - полное сопротивление цепи. Тогда выражение закона Ома примет вид:
, где Z - полное сопротивление цепи. Тогда выражение закона Ома примет вид:
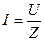 . (2.23)
. (2.23)
Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.23).
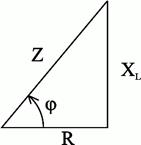
Рис.2.23. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью
Сдвиг фаз 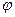 между током и напряжением определяется из треугольника сопротивлений:
между током и напряжением определяется из треугольника сопротивлений:
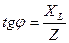 , (2.24)
, (2.24)
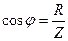 . (2.25)
. (2.25)
Поскольку вектор 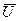 сдвинут по фазе относительно вектора
сдвинут по фазе относительно вектора 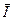 на угол
на угол 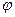 против часовой стрелки, этот угол имеет положительное значение.
против часовой стрелки, этот угол имеет положительное значение.
Если 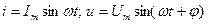 , то мгновенная мощность
, то мгновенная мощность 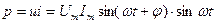 . Для действующих значений произведение
. Для действующих значений произведение 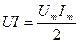 , откуда
, откуда 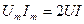 . Выражение
. Выражение 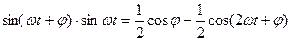 . Исходя из этого,
. Исходя из этого,
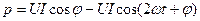 . (2.26)
. (2.26)
Таким образом, мгновенная мощность переменного тока может быть представлена в виде постоянной величины 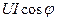 и, изменяющейся около неё с двойной частотой, величины
и, изменяющейся около неё с двойной частотой, величины 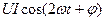 (рис. 2.24).
(рис. 2.24).
Введем понятие средней или активной мощности:
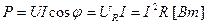 . (2.27)
. (2.27)
Активная мощность характеризует расход энергии на активном сопротивлении.
Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником:
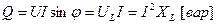 . (2.28)
. (2.28)
Полная мощность оценивает предельную мощность нагрузки:
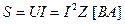 . (2.29)
. (2.29)
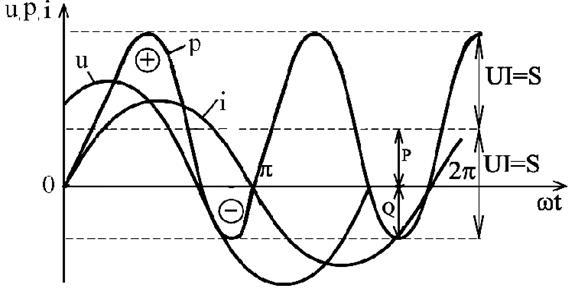
Рис.2.24. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью
Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.25).
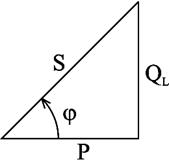
Рис.2.25. Треугольник мощностей
Так: 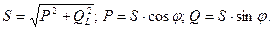 Обозначим коэффициент мощности в виде соотношения
Обозначим коэффициент мощности в виде соотношения 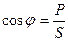 .
.
Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ.
Дата добавления: 2020-10-14; просмотров: 710;











