Графический метод расчета нелинейных цепей

Постоянного тока

Нелинейные цепи простой конфигурации удобно рассчитывать графическим методом. Рассмотрим графический метод расчета нелинейных цепей с последовательным и параллельным соединением нелинейных элементов.

Последовательное соединение НЭ. На рис. 7.4, а показано последовательное соединение двух НЭ, характеристики которых представлены на рис. 7.4, б.

а) б)

Рис. 7.4

Эти два элемента можно заменить одним эквивалентным (рис. 7.5) с вольт-амперной характеристикой I(U), построенной на рис. 7.4, б. Для построения этой характеристики, задаваясь значениями тока, суммируют значения напряжений U₁ и U₂ на нелинейных элементах в соответствии со вторым законом Кирхгофа. Полученная характеристика I(U) позволяет определить ток I' цепи для любого заданного значения входного напряжения U'. А по значению этого тока определить напряжения на НЭ U₁' и U₂' по вольтамперным характеристикам этих элементов.

Графические построения для расчета цепи (рис. 7.4, а) можно провести и другим методом (метод пересечения характеристик).

а) б)

Рис. 7.6

Напряжение U₂ на зажимах нелинейного элемента определяется, с одной стороны, вольт-амперной характеристикой этого элемента I₂(U₂), а с другой – характеристикой I(U – U₁), так как U₂ = U – U₁.

На рис. 7.6, а построены характеристики I(U₂) и I(U – U₁), абсциссы которых получены вычитанием абсцисс вольт-амперной характеристики I(U₁) из напряжения U при различных значениях тока.

Когда одним из элементов является линейное сопротивление R, построение упрощается. Как показано на рис. 7.6, б, прямая MN соответствует линейному уравнению U₂ = U – RI и построена по двум точкам, соответствующим режиму холостого хода (I = 0, U₂ = U') и режиму короткого замыкания (U₂ = 0, I = I_К = 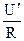) на участке цепи с НЭ.

Если последовательно с нелинейным элементом включен источник постоянной ЭДС (рис. 7.7, а), то ВАХ всей цепи получается путем смещения характеристики НЭ I(U₁) влево или вправо в зависимости от полярности источника (рис. 7.7, б). При этом положительное направление для напряжений выбирают совпадающим с положительным направлением тока.

а) б)

Рис. 7.7

Параллельное соединение нелинейных элементов показано на рис. 7.8, а. Характеристики этих НЭ представлены на рис. 7.8, б.

Эти два элемента можно заменить одним эквивалентным (рис. 7.9) с вольт-амперной характеристикой I(U), изображенной на рис. 7.8, а жирной линией. Для этого задаются произвольными значениями напряжения и суммируют соответствующие ординаты характеристик НЭ, то есть графически реализуют первый закон Кирхгофа: I=I₁+I₂.

а) б)

Рис. 7.8

Для нахождения токов в параллельно соединенных НЭ построение результирующей характеристики не требуется, так как токи находятся непосредственно по характеристикам НЭ.

Результирующая характеристика параллельно соединенных нелинейных элементов используется в том случае, если по заданному току I требуется определить напряжение U на зажимах цепи, а также при расчете цепей при смешанном соединении элементов.

Смешанное соединение НЭ. На рис. 7.10, а показана схема смешанного соединения НЭ.

Графическое построение для определения токов и напряжений приведено на рис. 7.10, б. Вначале производим замену двух параллельно соединенных элементов одним эквивалентным с характеристикой I₁(U₂) = (I₂ + I₃)(U₂).

Затем строим вольт-амперную характеристику I₁(U) всей цепи, задаваясь произвольными значениями тока I₁ и суммируя соответствующие абсциссы кривых I₁(U₂) и I₁(U₁).

Далее на оси абсцисс откладываем заданное напряжение U' и проводим прямую, параллельную оси ординат, до пересечения с кривой I₁(U) и на оси ординат находим ток I', соответствующий заданному напряжению. При этом значении тока по

кривой I₁(U₂) находим напряжение U₂', а по кривой I₁(U₁) –значение напряжения U₁'. По найденному значению напряжения U₂' на кривых I₂(U₂) и I₃(U₂) находим токи параллельных ветвей I₂' и I₃'.