Примеры решения задач

6.2.1 В электрической цепи, схема которой показана на рис. 6.6, происходит коммутация. Найти зависимость токов ветвей и напряжения индуктивной катушки от времени при переходном процессе.

Исходные данные U = 50 B, R₁ = R₂ = 100 Ом, L = 0,5 Гн.

Расчет переходных процессов в цепи будем выполнять согласно алгоритму, приведен-ному выше.

Покажем положительные направления токов и напряжений на элементах электрической цепи.

Электрическая цепь содержит индуктивную катушку, начальное значение тока которой определяется по первому закону коммутации. Поэтому определение переходных функций начнем с нахождения тока индуктивной катушки i_L(t). Остальные переходные функции найдем, используя законы Ома и Кирхгофа для мгновенных значений:

, , .

До замыкания ключа электрическая цепь была отключена от источника напряжения, и токи во всех ветвях отсутствовали. То есть в докоммутационной цепи ток индуктивной катушки i_L(0_-) = 0.

Согласно первому закону коммутации ток индуктивной катушки в момент коммутации не может измениться скачком и в первый момент остается равным докоммутационному значению i_L(0₊) = i_L(0_-) = 0.

Искомая переходная функция тока представляет собой сумму свободной и принужденной составляющей:

i _L(t) = i_Lсв(t) + i_Lпр.

Найдем принужденное значение тока катушки. Для этого рассчитаем величину тока в установившемся режиме в цепи после коммутации (рис. 6.7). В цепи постоянного тока в установившемся режиме идеальная индуктивная катушка представляет собой участок цепи с сопротивлением равным нулю, напряжение на зажимах которого так же равно нулю u_Lпр = 0. Так как катушка и резистор R₂ соединены параллельно, то есть напряжения на их зажимах одинаковы и равны нулю, то и принужденное значение тока второй ветви i_2пр= 0.

Принужденный ток катушки:

i_Lпр= i_1пр=U/R₁=50/100=0,5 А.

Для определения свободной составляющей необходимо составить характеристическое уравнение и найти его корни.

Составим характеристическое уравнение путем определения входного сопротивления Z(p) пассивной части цепи после коммутации (рис. 6.8). В рассматриваемой цепи источник напряжения заменяется короткозамкнутым участком, а индуктивная катушка операторным сопротивлением Lp. Наиболее целесообразно размыкать цепь на участке, который содержит реактивный элемент. В нашем случае находим входное сопротивление относительно разомкнутых зажимов ветви, содержащей индуктивную катушку:

.

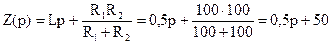Приравняв полученное выражение нулю, получим характеристическое уравнение:

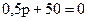, которое имеет один корень .

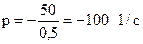Свободную составляющую тока катушки запишем . Для нахождения постоянной интегрирования А рассмотрим искомую функцию тока

i_L(t) = i_Lсв(t) + i_Lпр = 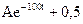в момент времени t = 0₊:

i_L(0₊)=А+0,5.

Так как согласно закону коммутации i_L(0₊) = 0, то получим уравнение А + 0,5 = 0, откуда найдем значение постоянной интегрирования А = –0,5 (А).

Переходная функция тока катушки i_L(t) = –0,5е^-100t+0,5 (А).

Напряжение индуктивной катушки:

Ток второй ветви:

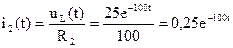(А).

Входной ток: =

= (–0,5е^-100t + 0,5) + 0,25е^-100t = –0,25e^-100t + 0,5 (A).

Временные зависимости токов и напряжения индуктивной катушки показаны на рис. 6.9, 6.10, 6.11. График переходного процесса строится на промежутке времени t = 5τ, так как за это время свободная составляющая переходной функции практически становится равной нулю и переходный процесс завершается. Постоянная времени τ = 1/|р| = 1/100 = 0,01 с.

6.2.2 В электрической цепи, схема которой показана на рис. 3.12, происходит коммутация. Найти зависимость от времени токов ветвей и напряжения конденсатора при переходном процессе.

Исходные данные: U = 100 B, R₁ = R₂ = 100 Ом, С = 10 мкФ.

На схеме указаны положительные направления токов и напряжений на всех элементах электрической цепи.

Электрическая цепь содержит конденсатор, начальное значение напряжения на котором определяется по второму закону коммутации. Поэтому определение переходных функций начнем с нахождения напряжения конденсатора u_C(t). Остальные переходные функции найдем, используя законы Ома и Кирхгофа для мгновенных значений:

, , .

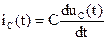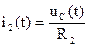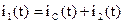До замыкания ключа электрическая цепь была отключена от источника напряжения, токи во всех ветвях отсутствовали и конденсатор не был заряжен. То есть в докоммутационной цепи напряжение конденсатора u_C(0_-) = 0.

Согласно второму закону коммутации напряжение конденсатора в момент коммутации не может измениться скачком и в первый момент остается равным докоммутационному значению u_C(0₊)=u_C(0_-)=0.

Искомая переходная функция напряжения конденсатора представляет собой сумму свободной и принужденной составляющей:

u _C(t) = u_Cсв(t) + u_Cпр.

Для определения принужденной составляющей рассчитаем установившееся значение напряжения конденсатора в схеме после коммутации (рис. 6.13). При составлении схемы для расчета принужденных значений необходимо помнить, что в установившемся режиме в цепи постоянного тока конденсатор представляет собой разомкнутый участок цепи.

В ветви с конденсатором ток не протекает i_Спр = 0, входной ток равен току второй ветви и определяется по закону Ома:

i_1пр= i_2пр= .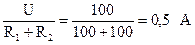

Напряжение конденсатора равно напряжению второй ветви, которая соединена с ним параллельно:

.

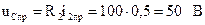Для составления характеристического уравнения найдем входное сопротивление Z(p) пассивной части схемы относительно любых разомкнутых зажимов. Источник напряжения заменим короткозамкнутым участком цепи, конденсатор – операторным сопротивлением 1/рС, а цепь разомкнем в той ветви, которая содержит конденсатор (рис. 6.14). Найдем операторное сопротивление:

.

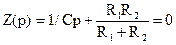Приравняв полученное выражение к нулю,

,

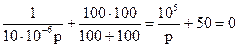получим характеристическое уравнение: 10⁵ + 50р = 0.

Полученное уравнение имеет один корень р = –2000 1/с.

Свободная составляющая состоит из одного слагаемого и находится как .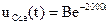

Определим постоянную интегрирования В. Для этого, рассмотрим искомую функцию напряжения:

u _C(t)=u_Cсв(t)+u_Cпр= в момент времени t=0₊:

u _C(0₊)= .

Согласно закону коммутации начальное значение напряжения конденсатора u_C(0₊) = 0.

Получим уравнение = 0, и найдем постоянную интегрирования В = –50 В.

Искомая переходная функция:

u _C(t) = 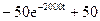(В).

Определим переходные функции токов ветвей:

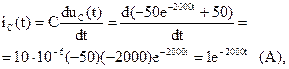
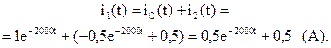
Временные зависимости полученных переходных функций построены на рис. 6.15 и 6.16. Время переходного процесса: t_пп = 5τ = 5/|р| = 5/2000 = 0,0025 с.

6.2.3 Катушка, индуктивность которой L_К = 5 Гн и активное сопротивление R_К = 4 Ом, отключается от источника постоянной ЭДС, напряжение которого U_Е = 110 В и замыкается на разрядный резистор сопротивлением R₁ = 6 Ом (рис. 6.17). Найти значение тока для момента времени t=1с после отключения катушки. Определить напряжение на резисторе R₁ в начальный момент после коммутации.

Когда переключатель находился в положении Ι, в цепи протекал постоянный ток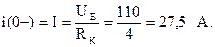

После коммутации, то есть перевода переключателя в положение II, катушка отключается от источника питания и поэтому принужденное значение её тока будет равно нулю.

Переходная функция тока катушки имеет только свободную составляющую: ,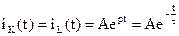

где постоянная времени:

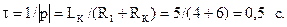
Найдем постоянную интегрирования А. Так как согласно первому закону коммутации, ток в катушке не может изменяться скачком, то в момент переключения t = 0:

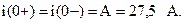
Выражение для переходного тока имеет вид:

При t = 1 с ток катушки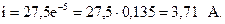

График переходного тока катушки показан на рис. 6.18.

Напряжение на разрядном реpиcторе R₁ в начальный момент после коммутации 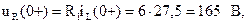то есть оно оказалось выше напряжения источника питания, так как R₁ > R_К. Указанное обстоятельство следует иметь в виду при коммутации цепей, содержащих индуктивные элементы, так как возникающие при этом перенапряжения могут вывести из строя аппаратуру.

6.2.4 Построить зависимость переходного напряжения на конденсаторе от времени в цепи рис. 6.19 при поочередном переключении выключателя в положения I и II. Напряжение U_BX = 5 В, R₁ = 75 Ом, R₂ = 25 Ом, С = 1 мкФ. Коммутация начинается с установки выключателя в положение I, время зарядки и разрядки конденсатора t = 4τ.

При установке переключателя в положение I в цепи возникает ток и конденсатор заряжается в течение времени t_зар = 4τ₁ = 4R₁C = 300 мкс.

Переходное напряжение на конденсаторе увеличивается по экспоненциальному закону:

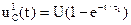
и через 300 мкс, то есть к моменту переключения выключателя в положение II, напряжение достигнет значения:

После установки выключателя в положение II начинается разрядка конденсатора от значения 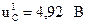, которая будет продолжаться в течении времени t_зар = 4τ₂ = 4R₂C = 100 мкс. При этом напряжение на конденсаторе будет изменяться в соответствии с экспоненциальной зависимостью .

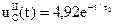Через 100 мкс оно снизится до 0,088 В. Кривая изменения напряжения на конденсаторе показана на рис. 6.20.

6.2.5 В цепи, схема которой приведена на рис. 6.21, происходит коммутация. Построить переходные функции напряжения и тока конденсатора. Данные для расчета Е = 20 В, R₁ = R₂ = R₃ = 10 Ом, R₄ = 30 Ом, С = 10 мкФ.

Определим, пользуясь заданным алгоритмом расчета переходных процессов, функцию изменения во времени напряжения конденсатора u _C(t)=u_Cсв(t)+u_Cпр.

Ток конденсатора рассчитаем по закону Ома, записанному для мгновенных значений: .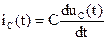

В установившемся докоммутационном режиме в ветви с конденсатором ток отсутствует и в цепи (рис. 6.22) в параллельных ветвях протекают токи:

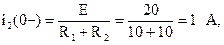
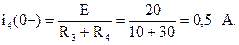
Напряжение конденсатора в докоммутационной цепи найдем по второму закону Кирхгофа:

Согласно второму закону коммутации напряжение конденсатора не может измениться скачком, поэтому начальное значение этого напряжения будет равно его докоммутационному значению:

u_C(0₊) = u_C(0_-)= –5 В.

Принужденное значение напряжения конденсатора определим, рассчитав токи и напряжения в установившемся режиме в цепи после коммутации (рис. 6.23). Ток в четвертом резисторе отсутствует и в цепи протекает только ток:

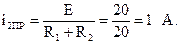
Тогда напряжение конденсатора:

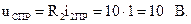
Составим характеристическое уравнение. Для этого найдем входное сопротивление пассивной части схемы после коммутации относительно разомкнутых зажимов ab (рис. 6.24). В рассматриваемой цепи источник напряжения заменяется короткозамкнутым участком, а конденсатор операторным сопротивлением 1/Сp:

.

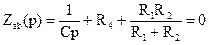Откуда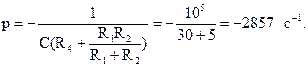

Характеристическое уравнение имеет один корень:

р = –2857 1/с,

поэтому свободную составляющую напряжения запишем как:

.

Определим постоянную интегрирования В. Для этого, рассмотрим искомую функцию напряжения:

u _C(t) = u_Cсв(t) + u_Cпр = 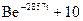в момент времени t = 0₊:

u _C(0₊) = .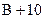

Начальное значение напряжения конденсатора u_C(0₊) = –5 В. Получим уравнение 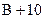= –5, и найдем постоянную интегрирования В = –15 В.

Искомая переходная функция напряжения:

u _C(t) = (В).

Определим переходную функцию тока в ветви с конденсатором:

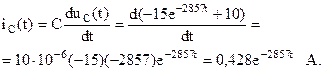
Графики переходных функций напряжения и тока конденсатора представлены на рис. 6.25.

6.2.6 В цепи, схема которой приведена на рис. 6.26, происходит коммутация. Построить переходные функции напряжения и тока индуктивной катушки.

Данные для расчета Е = 30 В, R₁ = R₂ = R₃ = 10 Ом, L = 1 мГн.

Определение переходных функций начнем с нахождения тока индуктивной катушки i_L(t). Напряжение на ее зажимах найдем, с помощью закона Ома для мгновенных значений:

.

Учитывая, что в цепи постоянного тока в установившемся режиме идеальная индуктивная катушка представляет собой участок с сопротивление равным нулю, легко определить ток катушки в схеме до коммутации (рис. 6.27):

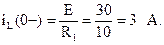
Согласно первому закону коммутации ток индуктивной катушки в момент коммутации не может измениться скачком и в первый момент остается равным докоммутационному значению

i_L(0₊) = i_L(0_-) = 3 А.

Искомая переходная функция тока представляет собой сумму свободной и принужденной составляющей i _L(t) = i_Lсв(t) + i_Lпр.

Найдем принужденное значение тока катушки. Для этого рассчитаем величину тока в установившемся режиме в цепи после коммутации (рис. 6.28). Так как индуктивная катушка представляет собой короткозамкнутый участок цепи, то ток в резисторе R₃ отсутствует, а ток катушки определим, как:

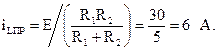
Составим характеристическое уравнение путем определения входного сопротивления Z(p) пассивной части цепи после коммутации (рис. 6.29). В рассматриваемой цепи источник напряжения заменяется короткозамкнутым участком, а индуктивная катушка операторным сопротивлением Lp. Находим входное сопротивление относительно разомкнутых входных зажимов цепи:

Характеристическое уравнение 1,5·10^-2р + 50 = 0 имеет один корень: р = –3333 1/с.

Свободную составляющую тока катушки запишем:

.

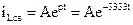Для нахождения постоянной интегрирования А рассмотрим искомую функцию тока: i_L(t)=i_Lсв(t)+i_Lпр= 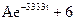в момент времени t = 0₊:

i_L(0₊)=А+6.

Так как согласно закону коммутации i_L(0₊) = 3 А, то получим уравнение А + 6 = 3, откуда найдем значение постоянной интегрирования А = –3 (А).

Переходная функция тока катушки: i_L(t)= –3е^-3333t+6 А.

Напряжение индуктивной катушки:

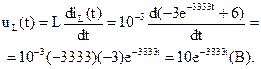
Графики переходных функций напряжения и тока конденсатора представлены на рис. 6.30.