Работа Т-образного фильтра
Рассмотрим работу Т- образного фильтра (рис. 2.12) в частотной области. Определим передаточную функцию фильтра
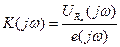
как отношение выходного сигнала фильтра 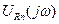 к гармоническому входному сигналу
к гармоническому входному сигналу 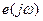 ,. В этом отношении величина
,. В этом отношении величина 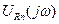 это напряжение на сопротивлении
это напряжение на сопротивлении 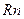 , а величина
, а величина 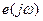 это напряжение входного сигнала.
это напряжение входного сигнала.
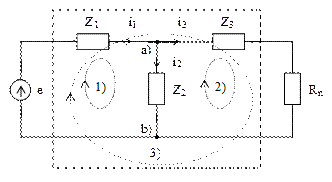
Рис. 2.12 – Контуры и узлы схемы Т-образного фильтра
Сопротивление схемы фильтра со стороны источника сигнала 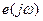 опишем следующим выражением
опишем следующим выражением
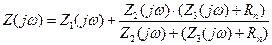
Ток схемы 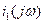 опишем выражением
опишем выражением
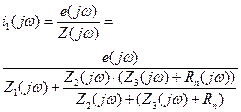
Напряжение 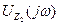 на сопротивлении схемы
на сопротивлении схемы 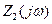 определяем выражением
определяем выражением
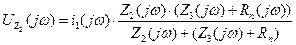
Ток схемы 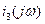 опишем выражением
опишем выражением
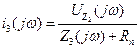
Напряжение 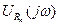 на сопротивлении нагрузки
на сопротивлении нагрузки 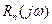 определяем выражением
определяем выражением
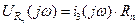
Передаточную функцию фильтра определяем следующим выражением
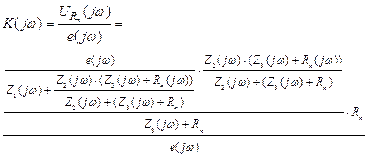
Проведя несложные преобразования, получим более простое выражение для передаточной функции фильтра
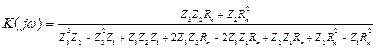
Рассмотрим работу Т- образного фильтра (рис. 2.12) во временной области. Запишем систему уравнений, используя первый и второй законы Кирхгофа, составленную по узлам и контурам схемы фильтра:
- для узлов а) и б) первый закон выглядит следующим образом 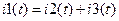 ;
;
- для контура 1), второй закон будет 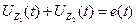 ;
;
- для контура 2), второй закон будет 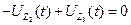 ;
;
- для контура 3), второй закон будет 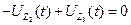 .
.
Пусть некоторой Т- образный фильтр задан схемой, представленной на рис. 2.13.
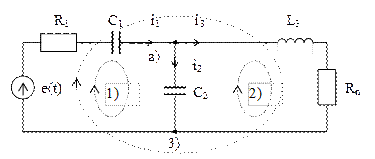
Рис. 2.13 – Пример схемы Т- образного фильтра
Сопротивления 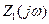 ,
, 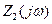 ,
, 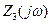 фильтра в частотной области выглядят следующем образом:
фильтра в частотной области выглядят следующем образом:
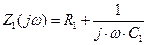 ,
,
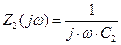 ,
,
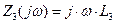 .
.
Для величин 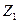 ,
, 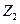 ,
, 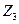 определенных в , , АЧХ и ФЧХ передаточной функции
определенных в , , АЧХ и ФЧХ передаточной функции 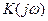 фильтра вычисляется по формуле с учетом величин
фильтра вычисляется по формуле с учетом величин 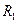 ,
, 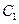 ,
, 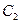 ,
, 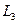 ,
, 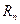 .
.
Графики АЧХ и ФЧХ передаточной функции 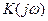 этого фильтра с величинами
этого фильтра с величинами 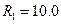 ,
, 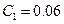 ,
, 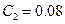 ,
, 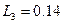 ,
, 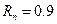 , построенные средствами пакета MathCAD, представлены на рис. г.3.
, построенные средствами пакета MathCAD, представлены на рис. г.3.
Для описания работы фильтра (рис. 2.13) во временной области составим систему интегро-дифференциальных и алгебраических уравнений (используя законы Ома и Кирхгофа). Для контуров 1), 2), 3) и узла а) система уравнений выглядит следующим образом:
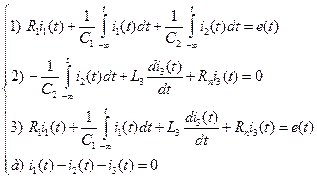 .
.
Независимые начальные условия уравнений определим по схеме фильтра для тока 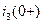 и напряжений
и напряжений 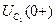 ,
, 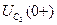 . Независимые начальные условия будут следующие:
. Независимые начальные условия будут следующие:
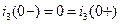 ,
,
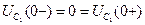 ,
,
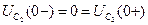 .
.
Зависимые начальные условия для уравнений токов 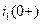 ,
, 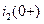 и производной
и производной 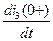 определим из уравнений , , . Зависимые начальные условия будут выглядеть следующим образом:
определим из уравнений , , . Зависимые начальные условия будут выглядеть следующим образом:
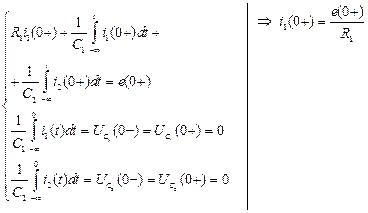 ,
,
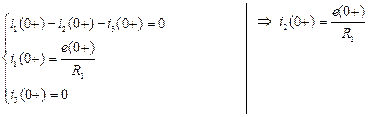 ,
,
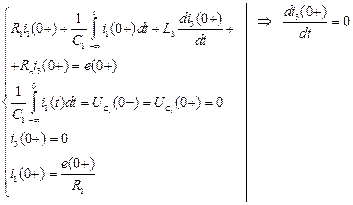 .
.
Дифференцируя, левые и правые части интегро-дифференциальных уравнений системы , получим систему с линейными неоднородными дифференциальными уравнениями с постоянными коэффициентами и алгебраическим уравнением
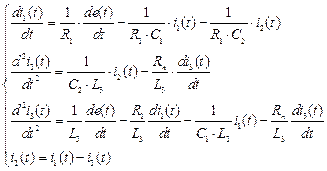 .
.
Так как в системе три дифференциальных уравнения являются линейно-зависимыми, то оставляем два дифференциальных уравнения (они будут линейно независимы) и оставляем алгебраическое уравнение. Таким образом, получаем систему из трех уравнений с тремя неизвестными
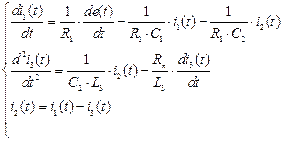
со следующими начальными условиями
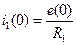 ,
, 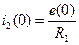 ,
, 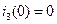 ,
, 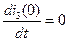 .
.
Введя дополнительную переменную 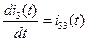 , получим следующую нормальную систему линейных неоднородных дифференциальных уравнений с постоянными коэффициентами
, получим следующую нормальную систему линейных неоднородных дифференциальных уравнений с постоянными коэффициентами
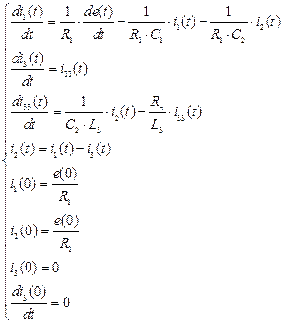 .
.
Решение системы уравнений средствами пакета MathCAD представлено на рис. г.4.
Дата добавления: 2020-10-14; просмотров: 370;











