Частотные характеристики фильтров
Выходной сигнал цепи n–го порядка можно определить через входной сигнал, линейным дифференциальным уравнением n–го порядка, имеющим следующий вид
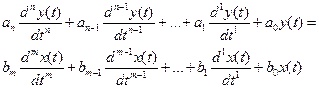 ,
,
где 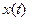 это входной сигнал, а
это входной сигнал, а 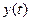 это выходной сигнал и
это выходной сигнал и 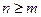 [ 4 ]. Применив к этому уравнению преобразование Лапласа, получим передаточную функцию фильтра
[ 4 ]. Применив к этому уравнению преобразование Лапласа, получим передаточную функцию фильтра 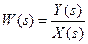 в виде отношения двух полиномов
в виде отношения двух полиномов 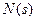 и
и 
 ,
,
где  представляет собой комплексную частоту, а
представляет собой комплексную частоту, а 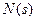 и
и  являются полиномами переменной
являются полиномами переменной 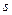 с вещественными коэффициентами
с вещественными коэффициентами 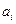 и
и 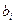 .
.
Записав полиномы 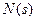 и
и  в виде сомножителей, получим полюсы и нули передаточной функции
в виде сомножителей, получим полюсы и нули передаточной функции
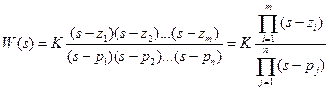 .
.
Полюсы 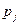 и нули
и нули 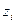 могут быть либо вещественными, либо комплексно-сопряженными. В том случае, когда числитель передаточной функции представляет собой постоянное число, считают, что его нули функции находятся в бесконечности.
могут быть либо вещественными, либо комплексно-сопряженными. В том случае, когда числитель передаточной функции представляет собой постоянное число, считают, что его нули функции находятся в бесконечности.
Пара комплексно сопряженных полюсов и нулей определяет передаточную функцию второго порядка
 ,
,
где 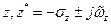 и
и  .
.
Полюсы и нули изображают на плоскости комплексной частоты или 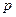 - плоскости (рис. 2.3). Очевидно, что
- плоскости (рис. 2.3). Очевидно, что 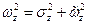 ,
, 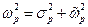 ,
, 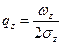 ,
, 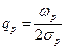 .
.
Следует отметить, что вещественные части полюсов и нулей 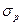 ,
, 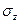 отображают на комплексной плоскости для определения частотных характеристик фильтров, а величины
отображают на комплексной плоскости для определения частотных характеристик фильтров, а величины  ,
, 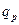 являются физически измеряемыми параметрами. Они отражают конструктивные особенности фильтров.
являются физически измеряемыми параметрами. Они отражают конструктивные особенности фильтров.
Для нахождения частотной характеристики цепи предполагают, что входной сигнал гармонический. Так как цепь линейна то выходной сигнал так же гармонический.

Рис. 2.3 – Полюсы и нули функции второго порядка
В этом случае осуществляют подстановку 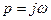 и получают
и получают
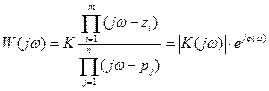 .
.
Логарифмируя частотную передаточную функцию, получим выражение
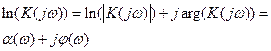 ,
,
где 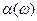 и
и 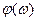 представляют АЧХ и ФЧХ (в неперах и градусах).
представляют АЧХ и ФЧХ (в неперах и градусах).
АЧХ в децибелах вычисляют по следующему правилу
 .
.
Характеристика группового времени замедления определяется следующим выражением
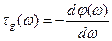 .
.
АЧХ и ФЧХ передаточной функции можно получить графически, используя ее полюсы и нули.
Для любой частоты  АЧХ и ФЧХ определяются из следующего выражения
АЧХ и ФЧХ определяются из следующего выражения
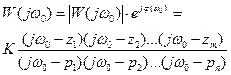 .
.
Каждый сомножитель в этом уравнении представляет собой вектор на комплексной плоскости
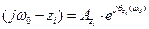 ,
,
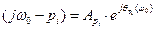 .
.
АЧХ и ФЧХ, учитывая , , примут следующий вид
 ,
,
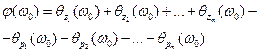 .
.
Рассмотрим, в качестве примера, следующую передаточную функцию
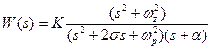 .
.
Нули и полюсы этой функции, расположенные на комплексной плоскости (рис. 2.4), определят амплитуду фазу выходного сигнала, на частоте  , следующим образом
, следующим образом
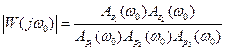 ,
,
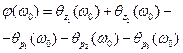 .
.
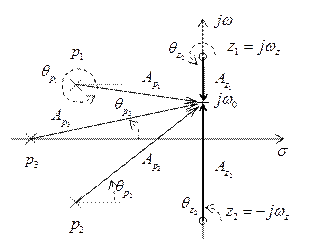
Рис. 2.4 – Полюсы и нули передаточной функции
Нули передаточной функции, расположенные на мнимой оси в точках 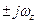 , определяют снижение АЧХ в этих точках до нуля т.к. при
, определяют снижение АЧХ в этих точках до нуля т.к. при 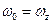
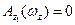 и следовательно
и следовательно 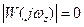 .
.
Дата добавления: 2020-10-14; просмотров: 291;










