Шифрование методом гаммирования

Определение 5.1.Под гаммированием понимают наложение на открытые данные по определенному закону гаммы шифра [8,20].

Определение 5.2.Гамма шифра – псевдослучайная последовательность, вырабатываемая по определенному алгоритму, используемая для зашифровки открытых данных и дешифровки шифротекста.

Общая схема шифрования методом гаммирования представлена на рис. 6.4.

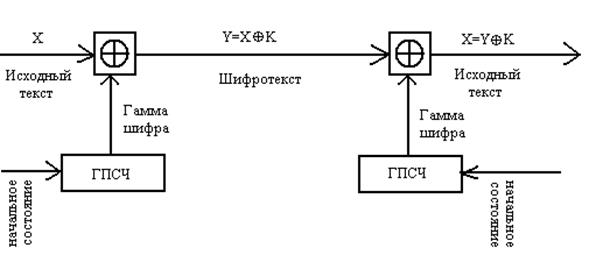
Рис. 6.4. Схема шифрования методом гаммирования

Принцип шифрования заключается в формировании генератором псевдослучайных чисел (ГПСЧ) гаммы шифра и наложении этой гаммы на открытые данные обратимым образом, например путем сложения по модулю два. Процесс дешифрования данных сводится к повторной генерации гаммы шифра и наложении гаммы на зашифрованные данные. Ключом шифрования в данном случае является начальное состояние генератора псевдослучайных чисел. При одном и том же начальном состоянии ГПСЧ будет формировать одни и те же псевдослучайные последовательности.

Перед шифрованием открытые данные обычно разбивают на блоки одинаковой длины, например по 64 бита. Гамма шифра также вырабатывается в виде последовательности блоков той же длины. Схему шифрования можно записать в этом случае в виде

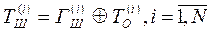
(5.9)

где 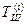- i-ый блок шифротекста, 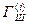- i-ый блок гаммы шифра, 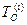- i-ый блок открытого текста, N – количество блоков открытого текста.

Дешифрование в данном случае осуществляется по следующей формуле:

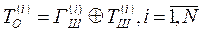
Стойкость шифрования методом гаммирования определяется главным образом свойствами гаммы – длиной периода и равномерностью статистических характеристик. Последнее свойство обеспечивает отсутствие закономерностей в появлении различных символов в пределах периода. Полученный зашифрованный текст является достаточно трудным для раскрытия в том случае, если гамма шифра не содержит повторяющихся битовых последовательностей. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого блока.

Обычно разделяют две разновидности гаммирования – с конечной и бесконечной гаммами. При хороших статистических свойствах гаммы стойкость шифрования определяется только длиной периода гаммы. При этом, если длина периода гаммы превышает длину шифруемого текста, то такой шифр теоретически является абсолютно стойким, т.е. его нельзя вскрыть при помощи статистической обработки зашифрованного текста, а можно раскрыть только прямым перебором. Криптостойкость в этом случае определяется размером ключа.

В настоящее время разработано множество алгоритмов работы генераторов псевдослучайных чисел, которые обеспечивают удовлетворительные характеристики гаммы. Рассмотрим несколько примеров данных алгоритмов.

Метод фон Неймана

Суть данного метода состоит в том, что каждое последующее случайное число получается путем возведения в квадрат предыдущего числа с отбрасыванием цифр младших и старших разрядов.

Пусть A₀ – четырехзначное число - начальное состояние ГПСЧ. Тогда i – ое псевдослучайное число А_i получается из предыдущего числа А_i-1 в результате следующих преобразований:

1. Возведение А_i-1 в квадрат, то есть нахождение числа .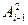

2. В качестве А_i выбирают четыре средние цифры числа .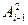

Пример 6.10.

Пусть A₀=1204, 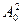=1449616. Тогда A₁=4496, 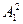=20214016, A₂=2140 и т.д

Однако метод фон Неймана является очень ненадежным, обладает множеством недостатков, в связи с чем, используется достаточно редко.

Линейный конгруэнтный метод

Данный генератор вырабатывает последовательность псевдослучайных чисел Y₁,Y₂,...,Y_i-1,Y_i,..., используя соотношение

где Y_i – i-ое (текущее) число последовательности; Y_i-1 – предыдущее число последовательности; a,b,m – константы; m – модуль; a – коэффициент; b – приращение; Y₀ – начальное состояние ГПСЧ.

Обычно значение модуля m берется равным 2ⁿ, либо простому числу. Приращение b должно быть взаимно простым с m, коэффициент a должен быть нечетным числом.

Линейный конгруэнтный метод является одним из самых простейших методов генерации псевдослучайных последовательностей. Существует ряд методов, формирующих намного более криптографически стойкие псевдослучайные последовательности.