Простые числа и их свойства
Определение 5.2.Натуральное число n>1 называется простым, если оно имеет в точности два различных натуральных делителя – 1 и n, в противном случае n называется составным.
Пример 5.4 Числа 2,3,7 являются простыми. Числа 4,6,8 – составными, так как их делителем является число 2.
Свойства простых чисел:
1. Если p1 и p2 – простые и 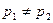 , то p1 не делится на p2.
, то p1 не делится на p2.
2. Пусть p – простое число, а n – натуральное, тогда n делится на p или наибольший общий делитель чисел n и p равен 1.
3. Если 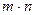 делится на простое число
делится на простое число 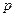 , то m делится на p или n делится на p.
, то m делится на p или n делится на p.
4. Если 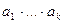 делится на простое число
делится на простое число 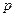 , то существует
, то существует 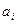 , которое делится на
, которое делится на 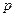 .
.
Известна следующая теорема:
Теорема 5.1.Любое натуральное число n>1 либо просто, либо раскладывается в произведение простых чисел и притом единственным образом с точностью до порядка следования сомножителей: 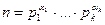 , где
, где 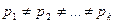 . Данное разложение называют канонической формой числа n.
. Данное разложение называют канонической формой числа n.
Задача представления числа n в канонической форме называется задачей факторизации числа n.
Существенный с точки зрения криптографии факт состоит в том, что в арифметике не известно эффективного алгоритма факторизации числа n. Никаких эффективных методов неизвестно даже в таком простом случае, когда необходимо найти два простых числа p и q, таких, что 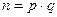 .
.
Известен ряд подходов, позволяющих выполнить проверку простоты целого числа n – решето Эратосфена, критерий Вильсона, тестирование на основе малой теоремы Ферма, тест Соловея-Штрассена, тест Рабина-Миллера и др.
Наибольшим общим делителем целых чисел a и b, обозначаемым как НОД(a,b) или просто (a,b), называют наибольшее целое, делящее одновременно числа a и b. Если (a,b)=1, то a и b называют взаимно простыми.
Числовые функции
В теории чисел и в криптографии большое значение имеют следующие числовые функции [8, 20].
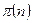 - определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая:
- определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая: 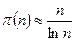 .
.
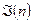 - определяет количество всех делителей числа n.
- определяет количество всех делителей числа n.
Пусть канонической формой числа n является 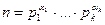 . Тогда
. Тогда 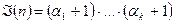 .
.
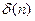 - определяет сумму всех делителей числа n,
- определяет сумму всех делителей числа n, 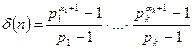
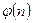 - функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,
- функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,
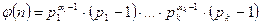
| (5.1) |
Пример 5.5
Для числа n=720 найдем 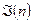 ,
, 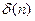 ,
, 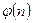 .
.
Представим число 720 в канонической форме - 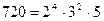 .
.
Тогда 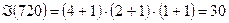
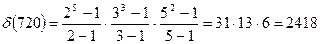
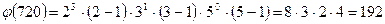
Выводы
Сравнимость по модулю, понятие простых, взаимно простых чисел, а также числовые функции имеют очень большое значение для криптографии, в частности при построении асимметричных шифров.
Вопросы для самоконтроля
1. Дайте определение сравнимости по модулю.
2. Приведите примеры чисел, сравнимых с 5 по модулю 7.
3. Что называют полным набором вычетов по модулю?
4. Перечислите основные свойства сравнений.
5. Дайте определение простого и составного числа. Приведите примеры.
6. Что называют канонической формой числа n.
7. В чем заключается задача факторизации числа n.
8. Факторизуйте следующие числа: 200, 143, 89.
9. Дайте определение наибольшего общего делителя чисел a и b.
10. Найдите наибольший общий делитель следующих чисел – 10 и 4, 20 и 21, 3 и 90.
11. Какие числа называют взаимно простыми? Приведите примеры взаимно простых чисел.
12. Найти 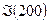 ,
, 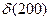 ,
, 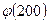 .
.
Дата добавления: 2020-10-14; просмотров: 628;











