Элементы теории чисел
При решении задач шифрования, дешифрования, построения ключевых систем в криптографии, используется представление обрабатываемого текста как целых чисел. Это дает возможность использовать математику целых чисел для создания стойких систем. Элементы теории целых чисел и рассматриваются в данной главе.
Модулярная арифметика
Пусть m – целое число. Тогда при делении любых целых чисел на m возможно получение ровно m остатков – 0,1,2,…,m-1.
Определение 5.1.Целые числа a и b называют сравнимыми по модулю m, если их разность a-b делится без остатка на m, или, что то же самое, остатки, получаемые при делении чисел a и b на m, равны между собой. В этом случае число b называют вычетом числа a по модулю m.
Если a сравнимо с b по модулю m, то это записывают как 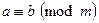 .
.
Пример 5.1
Целые числа 17 и 12 сравнимы между собой по модулю 5, то есть 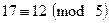 , кроме этого
, кроме этого 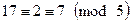 .
.
Существует бесконечное количество чисел, сравнимых с числом a по модулю m, но только одно из них расположено в диапазоне от 0 до m-1.
Обычно, для целого числа a>0 предпочитают использовать вычеты 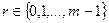 . Набор целых чисел от 0 до (m-1) называют полным набором вычетов по модулю m.
. Набор целых чисел от 0 до (m-1) называют полным набором вычетов по модулю m.
Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Целые числа по модулю m по отношению к операциям сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.
Основные свойства сравнений:
1. Рефлексивность: 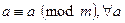 .
.
2. Симметричность: 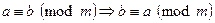 .
.
3. Транзитивность: 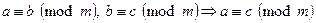 .
.
4. Если 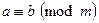 ,
, 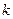 - произвольные целое число, то
- произвольные целое число, то 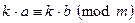 .
.
5. Если 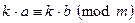 , наибольший общий делитель
, наибольший общий делитель 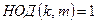 , то
, то 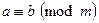 .
.
6. Если 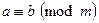 ,
, 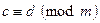 , то
, то 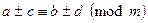 .
.
7. Если 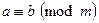 ,
, 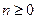 , то
, то 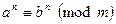 .
.
8. Если 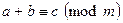 , то
, то 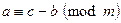 .
.
9. Если 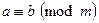 ,
, 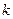 - произвольные целое число, то
- произвольные целое число, то 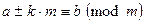 .
.
При выполнении арифметических операций по модулю, можно либо сначала приводить операнды по модулю m, а затем выполнять операции, либо сначала выполнять операции, а затем приводить результат по модулю m.
В криптографии используется множество вычислений по модулю m, так как с вычислениями по модулю удобнее работать в связи с ограничением диапазона всех промежуточных величин и результата. Кроме того, решение задач вида вычисления дискретных логарифмов трудно в вычислительном плане.
Для модуля m длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому такую операцию, как возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.
Возведение числа a в степень x по модулю m, то есть нахождение 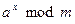 можно легко выполнить как ряд умножений. Особенно легко возводить в степень по модулю, если
можно легко выполнить как ряд умножений. Особенно легко возводить в степень по модулю, если 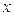 - степень двойки.
- степень двойки.
Пример 5.2
Пусть, например, требуется вычислить 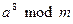 . В этом случае не следует выполнять серию умножений и одно приведение по модулю большого числа. Вместо этого выполняют три малых умножения и три малых приведения по модулю.
. В этом случае не следует выполнять серию умножений и одно приведение по модулю большого числа. Вместо этого выполняют три малых умножения и три малых приведения по модулю.
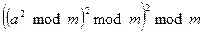
Например, 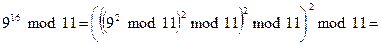
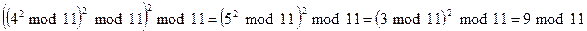
Вычисление 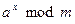 , где x не является степенью двойки, немного сложнее. В этом случае степень x представляют в двоичной форме и представляют x как сумму степеней двойки.
, где x не является степенью двойки, немного сложнее. В этом случае степень x представляют в двоичной форме и представляют x как сумму степеней двойки.
Пример 5.3
Пусть x=25(10)=11001(2), тогда 25=24+23+20.
Тогда
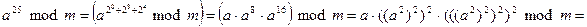
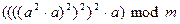 .
.
Поскольку многие алгоритмы шифрования основаны на возведении в большую степень больших чисел по большому модулю, целесообразно использовать рассмотренные выше алгоритмы быстрого возведения в степень.
Дата добавления: 2020-10-14; просмотров: 541;











