Помехоустойчивое кодирование
Кодированием в широком смысле называют любое преобразование сообщения в сигнал путем установления взаимного соответствия.
Пусть источник выдает некоторое дискретное сообщение А, которое можно рассматривать как последовательность элементарных сообщений или символов аi (i = 1, 2, . . . К). Совокупность символов аi называется алфавитом источника, а К – объемом алфавита.
Кодирование заключается в том, что каждый символ источника (сообщения) аi заменяется последовательностью кодовых символов – кодовой комбинацией. Совокупность правил, по которым образуется набор кодовых комбинаций, однозначно соответствующий алфавиту источника, называется кодом.
При кодировании отдельным символам аi удобно сопоставить целые числа от 0 до К-1, обозначив их, например, Mi
Любое число M может быть представлено в позиционной системе счисления с основанием m в виде
| M = bn-1mn-1 + bn-2mn-2 +. . . + b1m1 + b0m0. | (3.1) |
Основанием позиционной системы счисления называется количество символов в алфавите системы счисления, а в качестве коэффициентов bi в (3.1) могут использоваться только символы, входящие в алфавит этой системы, т.е. bi могут принимать значения 0, 1, . . . , m-1.
Тогда кодирующее преобразование можно отобразить так
| аi ® Mi ® (bn-1 bn-2 . . . b1 b0), | (3.2) |
где выражение в скобках представляет собой совокупность коэффициентов полинома (3.1), называемую кодовой комбинацией для аi. Такое преобразование является взаимно однозначным и обратимым, если не учитывать воздействия помех, что позволяет осуществлять декодирование.
Если число m символов в алфавите кода называется основанием кода. Число разрядов n в каждой кодовой комбинации постоянно при всех i, т.е. n=const, то такой код называется равномерным.
Необходимость замены каждого символа аi из К символов источника последовательностью кодовых символов или кодовой комбинацией (bn-1 bn-2 . . . b1 b0)объясняется тем, что в большинстве случаев объем алфавита K>m, т.е. основания кода или объема алфавита кодовых символов. Например, в телеграфном коде каждая буква русского алфавита (К=32) кодируется кодовой комбинацией из n=5 двоичных (m=2) символов (0 и 1).
Число возможных кодовых комбинаций из n разрядов для кода с основанием m равно N=mn . Если из этих N комбинаций для кодирования используется только часть, равная Nр, которые называются рабочими или разрешенными, то величина Nр называется мощностью кода.
Избыточность кода характеризуется коэффициентом избыточности
| rк = 1 - (logmNp / logmN). | (3.3) |
Код, у которого Nр = N, т.е. используются все возможные комбинации, имеет rк = 0 и называется безызбыточным или неизбыточным.
Простейшим безызбыточным равномерным кодом является обычный двоичный (m=2) n-разрядный код, называемый иногда кодом на все сочетания. Число комбинаций такого кода N = 2n.
При передаче кодовой комбинации безызбыточного кода по каналу связи в ней под воздействием помех возникают ошибки, но никаких признаков ошибочности принятая комбинация иметь не будет, поскольку вследствие безызбыточности любая подвергшаяся воздействию помех комбинация преобразуется в другую разрешенную или рабочую комбинацию.
Если при кодировании специальным образом вводить избыточность, то это приводит к увеличению возможностей по обнаружению и даже исправлению ошибок в принятых кодовых комбинациях. Такое кодирование называют помехоустойчивым или кодированием для канала.
Помехоустойчивый код отличается тем, что для кодирования используются не все возможные кодовые комбинации, которые можно сформировать из имеющегося количества разрядов, а лишь некоторые из них (искусственно вводимая избыточность), обладающие определенными свойствами и называемые разрешенными. Остальные, не используемые для кодирования символов источника кодовые комбинации, называются запрещенными.
Таким образом, все множество N=2n двоичных кодовых комбинаций, где n - число разрядов в комбинации, разбивается на два подмножества - разрешенных Nр и запрещенных N-Nр кодовых комбинаций. Если в результате воздействия помех передаваемая кодовая комбинация перейдет из подмножества разрешенных в подмножество запрещенных, ошибка будет обнаружена при приеме.
Коды, позволяющие определить только наличие ошибки, но не указывающие номера разряда, в котором она произошла, называются кодами с обнаружением ошибок.
Пусть, например, требуется передавать два сообщения - А1 и А2. Для этого достаточно одного двоичного разряда - А1 = 0, А2 = 1. Под воздействием помехи одно сообщение неминуемо преобразуется в другое.. Добавим к каждой кодовой комбинации еще по одному разряду, выбрав его значение таким, чтобы в каждой разрешенной кодовой комбинации было нечетное число единиц, т.е. А1 = 01, А2 = 10. Эти комбинации образуют подмножество разрешенных кодовых комбинаций. В подмножество запрещенных, следовательно, войдут комбинации, содержащие четное число единиц - 00 и 11. Одиночная ошибка может перевести сообщение А1 в 00 или в 11, аналогично и по отношению к сообщению А2, т.е. при наличии одиночной ошибки обе комбинации переходят в подмножество запрещенных, т.о. любая одиночная ошибка будет обнаружена.
При необходимости построения кода с исправлением ошибок все множество кодовых комбинаций N разбивается на Np непересекающихся подмножеств. Каждое из подмножеств приписывается одной из Np разрешенных кодовых комбинаций. Если передавалась кодовая комбинация Aj , принадлежащая подмножеству Nj , а принятой оказалась комбинация Ai , которая также принадлежит подмножеству Nj , то принимается решение о том, что принята комбинация Aj , т.е. ошибка исправляется. Если комбинация в результате воздействия помех перейдет в другое подмножество, то она будет принята с ошибкой.
Коды, которые не только обнаруживают ошибку, но и указывают номер разряда, в котором произошла ошибка, а для двоичных кодов это означает ее исправление, называются кодами с исправлением ошибок.
Для иллюстрации сказанного продолжим рассмотренный ранее пример, введя в использованные в нем кодовые комбинации еще один дополнительны разряд. В результате образуется множество из N=23 = 8 кодовых комбинаций. Его следует разделить на два (по числу передаваемых сообщений А1 и А2) непересекающихся подмножества. Пусть, например, для передачи А11 используется комбинация 001. Одиночная ошибка в любом из разрядов этой комбинации приведет к комбинациям А12 = 000, А13 = 011 и А14 = 101. Эти четыре комбинации и образуют первое подмножество. При приеме любой из них будет принято решение о том, что передавалось А1, т.е. любая одиночная ошибка будет исправлена. Аналогично относительно А2, если положить, что А21 = 110, то А22 = 111, А23 = 100, А24 = 010. При приеме любой из этих комбинаций будет принято решение, что передавалось А2.
Введением дополнительных разрядов в кодовые комбинации устанавливается нужное кодовое расстояние между разрешенными комбинациями. Из рассмотренных примеров можно, пока не обобщая, сделать вывод о том, что для обнаружения одиночной ошибки разрешенные кодовые комбинации должны различаться не менее, чем в двух разрядах, а для исправления одиночной ошибки - не менее, чем в трех разрядах. Под кодовым расстоянием или расстоянием Хэмминга понимается минимальное число позиций, на которых символы одной комбинации данного кода отличаются от символов другой комбинации этого же кода.
В общем случае для двоичных кодов расстояние между i-ой и j-ой комбинациями кода определяется по формуле
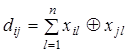
| (3.4) |
где xil – символ на l – ой позиции i – ой комбинации, xjl – символ на l – ой позиции j – ой комбинации, 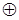 – символ суммирования по модулю два.
– символ суммирования по модулю два.
Формула (3.4) означает, что для определения расстояния между двумя кодовыми комбинациями необходимо просуммировать их по модулю два и подсчитать число единиц в полученной комбинации, оно и будет равно кодовому расстоянию между комбинациями.
Величина min dij = dmin , где минимум берется по всем комбинациям, входящим в данный код, называется кодовым расстоянием кода.
Множество n-разрядных кодовых комбинаций можно рассматривать как n-мерное векторное пространство, называемое кодовым пространством, а его элементы – кодовые комбинации, можно назвать кодовыми векторами. При таком подходе целесообразно ввести понятие вектора ошибки, который представляет собой n-разрядную комбинацию, в которой единица устанавливается в тех разрядах, номера которых соответствуют искаженным разрядам принятой кодовой комбинации.
Пусть, например, v1 = 11111 - переданный кодовый вектор, а v2 = 10111 - принятый кодовый вектор, тогда вектор ошибки е=01000.
| С этих позиций модель дискретного двоичного канала можно представить следующим образом. |

|
При теоретических исследованиях процесса возникновения ошибок в дискретном канале использую математические модели ошибок. Под математической моделью ошибки понимается распределение вероятностей по всем возможным векторам ошибок. Одной из наиболее часто встречающихся моделей ошибок является модель, основанная на следующей статистической гипотезе: «В каждом разряде вектора ошибки единица появляется с вероятностью p независимо от того, какие значения получили остальные разряды вектора ошибки».
Назовем величину, равную числу единиц в векторе ошибки, кратностью ошибки и обозначим ее символом q.
В теории вероятности доказано, что выдвинутой статистической гипотезе отвечает биномиальный закон распределения кратности ошибки. Таким образом, для рассматриваемого примера математической моделью ошибки может служить формула Бернулли
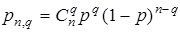
| (3.5) |
Здесь pn,q – вероятность того, что при передаче по дискретному каналу в кодовой комбинации двоичного кода с разрядностью n возникнет ошибка кратности q.
Используя (3.5) можно получить следующие выражения для вероятности ошибочного декодирования род при исправлении ошибок
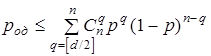
и для вероятности необнаруженной ошибки рно при обнаружении ошибок
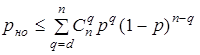 .
.
Здесь [d/2] означает целую часть d/2 . Знак неравенства в этих выражениях ставится потому, что код, вообще говоря, может исправлять некоторые ошибки кратности d/2 и выше и обнаруживать ошибки кратности d и выше.
Неравенства, приведенные выше, иллюстрируют важную роль кодового расстояния d как основного показателя исправляющих и обнаруживающих свойств кода - чем больше d, тем меньше род и рно.
Пример 3.1. Определить вероятность возникновения ошибок кратности q=0,1,2,3,4,5 в кодовой комбинации длины n=5 двоичного кода, если вероятность ошибочного приема разряда p=0,1. Определить вероятность ошибочного приема кодовой комбинации.
Решение. В качестве ответа на первый вопрос вероятности, вычисленные по формуле (3.5) сведем в таблицу
| q | 0 | 1 | 2 | 3 | 4 | 5 |
| p5,q | 0,56 | 0,33 | 0,07 | 0,008 | 0,0004 | 0,00001 |
Из таблицы видно, что вероятность появления ошибок большой кратности мала. Наиболее часто появляются однократные ошибки.
Для ответа на второй вопрос воспользуемся формулой 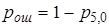 , где p5,0 - вероятность безошибочного приема. Тогда
, где p5,0 - вероятность безошибочного приема. Тогда 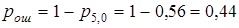 .
.
Следует учесть, что эффективность кода в смысле помехоустойчивости зависит от вида помех, действующих в канале. Код может быть очень хорошим при одной статистике помех и очень плохим - при другой. Поэтому при выборе помехоустойчивых кодов следует ориентироваться на определенный вид помех и в соответствии с ним выбирать определенную модель ошибок, которая может отличаться от рассмотренной в примере.
При выполнении статистической гипотезы о том, что ошибки меньшей кратности появляются чаще ошибок большей кратности, определяют максимальную кратность qmax ошибки, начиная с которой, исходя из требований к верности передачи, все ошибки меньшей кратности должны обнаруживаться помехоустойчивым кодом. По максимальной кратности ошибки qmax выбирают такое кодовое расстояние, при котором все разрешенные кодовые комбинации под действием ошибок кратностью не более qmax переходят в подмножество запрещенных и, следовательно, обнаруживаются.
Результатом действия ошибки кратностью qmax на разрешенную кодовую комбинацию будет новая кодовая комбинация, удаленная от первой на расстояние qmax. Отсюда ясно, что для обнаружения всех ошибок кратностью не превышающей qmax кодовое расстояние должно быть d> qmax, по крайней мере
| d = qmax + 1 . | (3.6) |
В теории кодирования доказывается, что для обеспечения возможности исправления ошибок кратности не более qmax кодовое расстояние должно быть больше 2qmax. Обычно оно выбирается по формуле
| d = 2qmax + 1 . | (3.7) |
Рассмотрим одну из возможных классификаций избыточных корректирующих кодов (рис. 3.1).
1. Так же как и неизбыточные, избыточные коды могут быть подразделены на равномерные и неравномерные. Признаком равномерности является то, что в каждой кодовой комбинации содержится n = const разрядов. Неравномерные коды получили существенно меньшее распространение.

|
| Рисунок 3.1. Классификаций избыточных корректирующих кодов |
2. Если каждый символ сообщения кодируется, т.е. превращается в кодовую комбинацию (блок) независимо от других символов сообщения, так, что закодированная последовательность символов представляет собой последовательность независимых кодовых комбинаций одинаковой длины, то такой код называют блоковым. Если кодирование каждого символа сообщения зависит от предшествующих или последующих символов, так, что закодированная последовательность представляет собой одно полубесконечное слово, то такой код называется непрерывным. Эти коды появились сравнительно недавно, но бурно развиваются.
3. Если в каждой кодовой комбинации длины n блокового кода можно выделить k разрядов, предназначенных собственно для передачи информации и называемых информационными, и n-k разрядов избыточно введенных для увеличения кодового расстояния кода с целью придания ему корректирующих свойств, то такой код называется разделимым. Эти n-k разрядов называются контрольными или проверочными. Если такого разделения разрядов кодовой комбинации по их функциональному назначению произвести нельзя, то такой код называется неразделимым.
4. Если в разделимом коде при кодировании информационные символы не изменяются, то такой код называется систематическим. В противном случае, т.е. когда при кодировании изменяются не только проверочные, но и информационные разряды, код называется несистематическим. Характерной особенностью большинства систематических кодов является то, что проверочные n-k разрядов кодовой комбинации представляют собой результаты определенных линейных операций над k информационными разрядами. Такие коды называются линейными. Линейные коды образуют векторное пространство и обладают следующим важным свойством: две кодовые комбинации можно сложить (для двоичных кодов - по модулю два), в результате чего получится третья кодовая комбинация этого же кода. Это свойство приводит к двум важным следствиям. Первое - каждая кодовая комбинация выражается в виде линейной комбинации небольшого числа выделенных кодовых комбинаций, называемых базисными векторами. Это существенно упрощает как описание кода (матричное описание), так и процедуры кодирования и декодирования. Второе - линейность существенно упрощает вычисление параметров кода, в частности, кодового расстояния. Расстояние Хэмминга между данной кодовой комбинацией и нулевой кодовой комбинацией равно числу ненулевых элементов в данной кодовой комбинации. Это число часто называют весом Хэмминга данной кодовой комбинации. Список, содержащий число кодовых комбинаций каждого веса, называют спектром кода.
5. Из класса систематических кодов можно выделить еще один подкласс кодов, называемых циклическими. Характерной особенностью циклических кодов, при сохранении всех свойств систематических кодов, является то, что если комбинация принадлежит циклическому коду, то комбинация, полученная из первой путем циклического сдвига, тоже будет принадлежать этому коду.
Все рассмотренные выше коды являются избыточными, т.е. такими, у которых d ³ 2. В зависимости от величины d коды подразделяются на коды, только обнаруживающие ошибки, и коды исправляющие ошибки.
Рассмотрим некоторые простейшие блоковые коды с обнаружением ошибок.
Дата добавления: 2020-10-14; просмотров: 660;











