Лекция 8. Методы импульсной и цифровой модуляции. Стандарты физического уровня

В качестве переносчика при импульсных видах модуляции используется периодическая (с периодом Т) последовательность импульсов с исходной амплитудой U и длительностью импульса t (рис. 2.18).

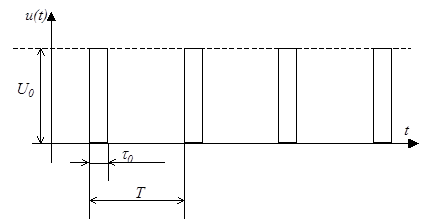
Рисунок 2.18. Импульсная несущая

При АИМ под воздействием модулирующего сигнала изменяется амплитуда переносчика. Если амплитуда импульса принимается равной мгновенному значению модулирующей функции в момент начала импульса и остается таковой в течение всей длительности импульса, то такую АИМ принято называть АИМ-2 (рис. 2.19).

Рисунок 2.19. Амплитудно-импульсная модуляция

При АИМ-1 происходит изменение прямоугольной формы импульсов несущей, выражающееся в том, что крыши импульсов повторяют закон изменения модулирующего сигнала в соответствующие интервалы времени.

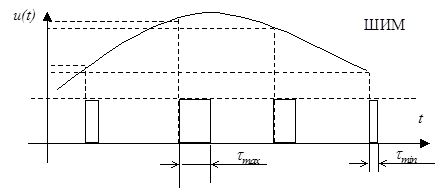
При использовании ШИМ под действием мгновенных значений модулирующего сигнала изменяется длительность (t) или другими словами, ширина импульса несущей, расширяясь при увеличении и сужаясь при уменьшении мгновенных значений модулирующего сигнала (рис. 2.20).

Рисунок 2.20. Широтно-импульсная модуляция

Существует несколько разновидностей ШИМ, отличающихся тем, что указанное изменение ширины импульса могут происходить за счет изменения положения заднего фронта импульса, или переднего фронта, или обоих фронтов.

При ФИМ изменяется положение импульсов несущей относительно т.н. тактовых точек в зависимости от мгновенного значения модулирующего сигнала (рис. 2.21).

Рисунок 2.21. Фазо-импульсная модуляция

При ЧИМ в зависимости от мгновенного значения модулирующего напряжения изменяется частота следования импульсов несущей

Рассмотрение спектров сигналов с импульсными видами модуляции начнем с того, что запишем выражение для спектра несущей

,

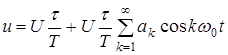где U – амплитуда импульса, t – длительность импульса, Т– период последовательности импульсов, 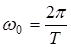– круговая частота импульсов, 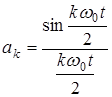– относительные амплитуды гармоник.

Предположим, что последовательность импульсов модулируется гармоническим первичным сигналом 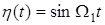по амплитуде, т.е. амплитуда импульсов изменяется по закону .

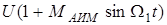Тогда после подстановок и преобразований получим

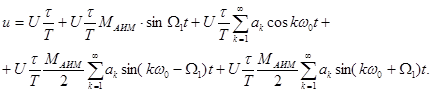
Таким образом, спектр АИМ – сигнала содержит (рис. 2.22):

1) постоянную составляющую;

2) составляющую с частотой модулирующего сигнала W₁;

3) бесконечное число составляющих с частотами, кратными основной частоте w₀, каждая из которых имеет;

4) верхнюю с частотой kw₀+W₁ и нижнюю с частотой kw₀- W₁ боковые составляющие.

Так как в спектре есть составляющая с частотой модулирующего сигнала W₁, то выделить модулирующий сигнал из АИМ – сигнала можно с помощью ФНЧ.

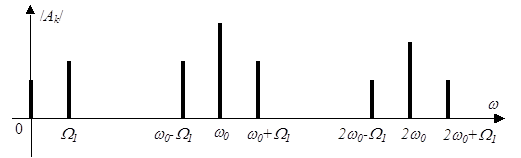
Рисунок 2.22. Спектр АИМ-сигнала

Если последовательность импульсов модулируется не простым гармоническим сигналом, а некоторым первичным сигналом, ширина спектра которого W_min - W_max, то в спектре частот АИМ – сигнала появятся не отдельные спектральные линии, а полосы частот.

В этом случае первичный сигнал можно выделить из АИМ – сигнала с помощью ФНЧ только в том случае, если полоса частот W_min - W_max не перекрывается полосой (w₀- W_max) – (w₀- W_min). А это возможно только в том случае, если частота следования импульсов w₀ по меньшей мере вдвое больше W_max.

Практически необходимая ширина спектра при АИМ мало зависит от модулирующего сигнала и полностью определяется параметрами несущей, т.е. длительностью t импульсов и скважностью Т/t импульсной последовательности.

Спектры сигналов при остальных видах импульсной модуляции будут отличаться от спектра АИМ- сигнала тем, что около составляющей с основной частотой 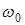и ее высших гармоник 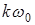появляется не по одной верхней и нижней боковой, а дискретные полосы боковых гармоник с частотами .

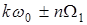Сравнивая рассмотренные методы импульсной модуляции по помехоустойчивости можно сделать следующие выводы. Наименьшей помехоустойчивостью обладает АИМ. Поэтому АИМ для передачи непосредственно не применяется, хотя и используется в качестве предварительной операции в системах в временным разделением каналов.

Сравнивая ФИМ и ШИМ, можно сказать, что при одинаковой полосе пропускания тракта помехоустойчивость ФИМ и ШИМ одинакова. Однако при ШИМ средняя мощность сигнала больше, чем при ФИМ, так как для обеспечения возможности модуляции ширины импульса среднюю длительность импульса при ШИМ приходится брать большей, чем при ФИМ. Следовательно, при сохранении средней мощности сигнала, переход к ФИМ дает возможность увеличить амплитуду импульса и тем самым увеличить отношение сигнал/помеха на входе приемника.

Кроме того, при ШИМ длительность импульсов по сравнению с исходной t может увеличиваться и уменьшаться. Если длительность импульса в процессе модуляции уменьшается значительно, т.е. имеет место большая глубина ШИМ, то соответственно расширяется практически необходимая полоса частот для передачи.

Таким образом, при ШИМ ширина полосы пропускания тракта передачи должна обеспечивать достаточно малые искажения наиболее короткого импульса, т.е. она оказывается более широкой, чем требуется для импульса средней длительности. При ФИМ длительности всех импульсов одинаковы, что позволяет выбрать оптимальную ширину полосы пропускания.

Таким образом, ФИМ характеризуется рядом преимуществ по сравнению с другими видами импульсной модуляции, благодаря чему она применяется в большинстве систем импульсной связи.

Наиболее известными методами цифровой модуляции являются:

1) импульсно- кодовая модуляция (ИКМ);

2) ИКМ с предсказанием, среди разновидностей которой чаще используется дифференциальная ИКМ (ДИКМ);

3) дельта-модуляция (ДМ).

ИКМ является наиболее простым методом цифровой модуляции. Суть ее состоит в том, что отсчеты сигнала, т.е. АИМ - импульсы квантуются по уровню, а затем кодируются с помощью того или иного кода. Кодирование состоит в замене по определенному правилу каждого из импульсов с квантованной амплитудой кодовой комбинацией из двоичных символов (рис. 2.23).

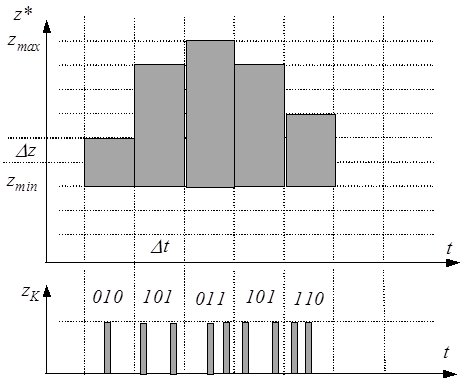
Рисунок 2.23. Принцип ИКМ

Одной из причин, приводящих к отличию принятого сообщения от переданного, в системе с ИКМ является шум квантования, другой – помехи в канале, которые воздействуют на передаваемую кодовую комбинацию и могут вызвать ошибки.

Ошибки в символах кодовых комбинаций при отсутствии в ней избыточности приводят к ошибочному декодированию всей кодовой комбинации. В результате ошибочного декодирования действительно переданное значение отсчета заменяется другим, причем не обязательно ближайшим, поскольку это зависит от того, какие символы кодовой комбинации приняты с ошибкой. Назовем эту составляющую шума шумом ложных импульсов. При оценке помехоустойчивости систем с ИКМ необходимо учитывать суммарный шум, состоящий из шума ложных импульсов и шума квантования. Однако в правильно спроектированной системе с ИКМ мощность сигнала превышает пороговую, при которой соотношение «сигнал/шум ложных импульсов» таково, что шумом ложных импульсов по сравнению с шумом квантования можно пренебречь.

Шум квантования не связан с помехами в канале и полностью определяется выбором числа уровней квантования. Его можно сделать сколь угодно малым, увеличивая число уровней квантования. Но при этом придется увеличивать число разрядов в кодовой комбинации, а, следовательно, сокращать длительность битового интервала, что приведет к расширению спектра сигнала.

Поскольку непосредственное измерение шума квантования затруднительно, то для его оценки используются расчетные методы, в соответствии с которыми, например, с переходом от 128 уровней квантования к 256 шум квантования уменьшается на 6 дБ. При этом вместо семи символов в кодовой комбинации будет восемь символов, так что длительность битового интервала уменьшиться в 8/7~1,14 раза, во столько же раз увеличиться ширина спектра сигнала. При этом необходимо учитывать еще одно обстоятельство. Величина шума ложных импульсов и связанная с ней вероятность ошибки зависят от энергии элемента сигнала, следовательно, при уменьшении его длительности придется увеличивать во столько же раз его мощность, чтобы она превышала пороговую.

Воздействие шума квантования можно заметно уменьшить, применяя неравномерное квантование, при котором входные сигналы с большим значением квантуются с большим шагом, а с малым значением – с меньшим шагом. Одним из способов получения неравномерного квантования является квантование с компандированием сигнала. Компандерная система представляет собой комплекс из двух нелинейных преобразователей с взаимно обратными амплитудными характеристиками (рис. 2.24).

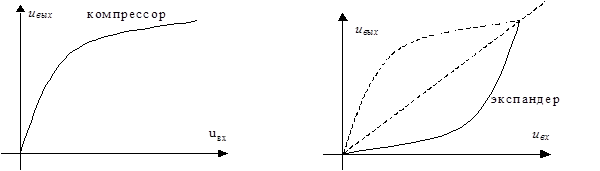
Рисунок 2.24. Амплитудные характеристики компрессора и экспандера

Преобразователь, устанавливаемый на передающей стороне, называется компрессором, а второй, устанавливаемый на приемной стороне, называется экспандером.

Компрессор слабые сигналы усиливает в большей степени, чем сильные, в результате чего происходит сжатие динамического диапазона сигнала, после чего такой сигнал равномерно квантуется и кодируется. Комбинация операций сжатия динамического диапазона и равномерного квантования эквивалентна нелинейному квантованию, причем закон изменения шага квантования определяется амплитудной характеристикой компрессора. Доказано, что требуемая форма амплитудной характеристики компрессора, при которой защищенность сигнала от шума квантования для всех значений сигнала остается постоянной, должна иметь вид:

,

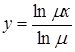где 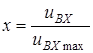, , 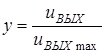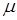– параметр компрессора, характеризующий кривизну его амплитудной характеристики. Реализовать такую характеристику при малых значениях 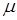невозможно. Поэтому используют близкие к ней амплитудные характеристики компандирования, отличающиеся начальным участком:

1) характеристика компандирования типа :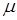

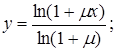
2) характеристика компандирования типа А:

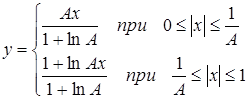
После кодирования и передачи на приемной стороне производится обратное преобразование, т.е. сначала восстанавливаются отсчеты с равномерным шагом квантования, а затем они подвергаются экспандированию, при котором восстанавливается исходный динамический диапазон сигнала.

Искажения, вызванные этими преобразованиями, будут отсутствовать только в том случае, если суммарная амплитудная характеристика системы «компрессор – экспандер» будет линейной.

Для иллюстрации влияния компандирования можно привести такой расчетный пример. При коэффициенте сжатия (коэффициентом сжатия называется отношение максимального шага квантования к минимальному), равном 100 и восьмиразрядном кодировании отношение «сигнал/шум квантования» составляет около 30дБ в динамическом диапазоне входных сигналов 40 дБ. Для получения такого же результата без компандирования пришлось бы перейти от восьмиразрядного к 12-разрядному кодированию, о последствиях чего говорилось ранее.

Рассмотренный метод аналогового компандирования использовался лишь в первом поколении ИКМ- систем (ИКМ-12). В последующих системах применялось цифровое компандирование, которое может быть реализовано двумя методами: 1) с равномерным квантованием и цифровым компрессором на выходе; 2) с цифровым устройством управления, которое обеспечивает выбор уровней квантования в соответствии с заданным законом компрессирования, т.е. непосредственно неравномерное квантование.

Из описанного принципа реализации ИКМ следует, что каждый отсчет сигнала кодируется отдельно и независимо от других и, соответственно, каждая кодовая комбинация несет информацию только об одном отсчете сигнала. Значения отсчетов берутся через интервал, определяемый теоремой Котельникова.

Суть теоремы Котельникова состоит в том, что функцию s(t) с финитным спектром можно точно восстановить по ее отсчетам s(kDt), взятым через интервалы времени Dt=1/2f_в, где f_в - верхняя частота спектра функции. Это осуществляется с помощью разложения функции в ряд Котельникова

.

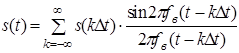Функции 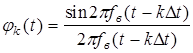, образующие базис Котельникова, называют функциями отсчета. Они отличаются друг от друга только сдвигом по оси времени (рис. 2.25) на интервалы, кратные Dt.

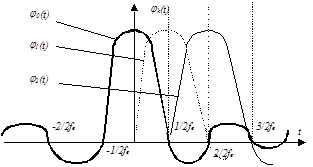
Рисунок 2.25. Функции отсчета

Они отличаются друг от друга только сдвигом по оси времени на интервалы, кратные Dt. При t=nDt, где n - любое целое число, все функции отсчета равны 0, кроме j_n, которая равна 1.

Фундаментальное значение теоремы Котельникова состоит в том, что она, во-первых, позволяет заменить исследование непрерывных процессов более простой задачей исследования дискретных процессов. Во-вторых, она позволяет наряду с частотным представлением процессов (разложение в гармонический ряд Фурье, спектральные функции) применять и временное представление - разложение во временной ряд Котельникова.

Однако применение этой теоремы встречает некоторые трудности. Строго говоря, функция с ограниченным спектром не ограничена (не финитна) во времени и, наоборот, финитная функция времени имеет неограниченный спектр.

На практике часто приходится иметь дело с сообщениями и сигналами конечной длительности, энергия или мощность которых почти полностью сосредоточена в интервале времени от Т₁ до Т₂ и в полосе частот DF = f_в - f_н. Слово «почти» оправдывает применение к этим объектам теоремы Котельникова и позволяет представлять их не бесконечным рядом, а конечной суммой. Естественно, такое представление уже не является точным и выполняется с некоторой погрешностью.

Будем полагать, что вся энергия сигнала содержится в полосе частот до f_в, а все отсчеты за пределами интервала (Т₁, Т₂) равны нулю. Тогда

.

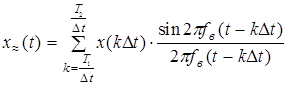Ограничение членов ряда конечным числом приводит к появлению ошибки, абсолютное значение которой равно

,

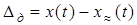а относительное

,

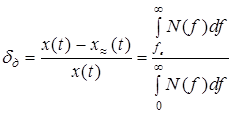где знаменатель представляет собой полную мощность сигнала x(t), а числитель – часть его мощности, отброшенную при введении ограничения по времени и ограничения по спектру.

Не смотря на наличие указанной погрешности, достоинство такого преобразования состоит в переходе от бесконечномерного пространства к конечномерному пространству сигналов, т.е. сигналов, финитных и по спектру и по времени. Размерность этого пространства определяется числом элементов суммы 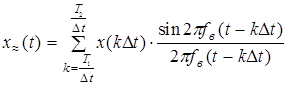, которое равно 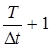или .

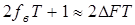Эту величину 2DFT называют базой сигнала. Физически она указывает на количество отсчетов, необходимых для описания сигнала.

Значения отсчетов, взятых через интервал, определяемый теоремой Котельникова, взаимно некоррелированы только в том случае, если спектр сообщения в занимаемой им полосе частот равномерен. На практике чаще передаются сообщения с неравномерным спектром, кроме того, частоту отсчетов по ряду соображений выбирают несколько больше, чем по теореме Котельникова. В связи с этим корреляция между отсчетами обычно не равна нулю.

При использовании классической ИКМ корреляционные связи, которые имеются в сигнале, никак не влияют на процесс кодирования и поэтому необходимое число уровней квантования при выбранном шаге квантования определяется только динамическим диапазоном сигнала. Ясно, что при наличии корреляции между значениями сигнала в моменты дискретизации можно уменьшить требуемое число уровней квантования и снизить при этом требуемую пропускную способность канала, не увеличивая мощность шума квантования, либо, сохраняя неизменным число уровней квантования, уменьшить мощность шума квантования.

Эта идея реализована в т.н. ИКМ с предсказанием.

Последовательность отсчетов a(i) подается на один вход вычитающего устройства, на второй вход которого подается сигнал предсказания 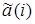, сформированный из предыдущих отсчетов по определенному правилу. Полученный таким образом разностный сигнал Da и подается в тракт передачи. Поскольку именно в разностном сигнале содержатся новые сведения, представляющие собой разность между истинным и предсказанным значениями, то такой способ получил название ИКМ с предсказанием. Поскольку на приемной стороне имеется такой же предсказатель, оперирующий с теми же предыдущими отсчетами, то и предсказанное им значение нового отсчета будет таким же, как на передающей стороне. Добавив к нему полученное из тракта передачи значение разностного сигнала, можно восстановить истинный отсчет.

Если разностный сигнал определяется по правилу Da(i)= a(i) - a(i-1), а затем квантуется и кодируется, то такой метод носит название дифференциальной ИКМ (ДИКМ).

Поскольку значения приращений сигнала Da значительно меньше значений самих отсчетов a, то шкала квантования разностного сигнала будет содержать меньшее число уровней и требуемая скорость передачи окажется ниже, чем в классической ИКМ.

Поскольку мощность шума квантования составляет вполне определенную долю мощности квантуемого процесса, а мощность разностного сигнала, как правило, меньше мощности отсчетов, шум квантования при ДИКМ меньше, чем при обычной ИКМ при том же числе уровней квантования.

Наибольшим искажениям от шума квантования подвергаются разностные сигналы малой величины. Для уменьшения этих искажений применяется неравномерное квантование, при котором шаг квантования возрастает по мере увеличения значения разностного сигнала. Такой метод называется адаптивной ДИКМ (АДИКМ), поскольку при этом происходит адаптация величины шага квантования к параметрам квантуемого сигнала.

При использовании ДИКМ возможно появление специфического вида искажений, называемых перегрузкой по крутизне. Если число уровней и шаг квантования выбраны таким образом, что максимальная разность, которая может быть закодирована, равна Da_max, а очередная полученная разность Da>Da_max, то эта разность передается с ошибкой, которая вызовет искажения формы восстановленного на приемной стороне сигнала. Этот вид искажений и называется перегрузкой по крутизне.

Анализ показывает, что в общем случае ДИКМ обеспечивает одинаковое с ИКМ качество передачи при меньшем числе символов в кодовой комбинации, соответствующей отсчету сигнала.

Существенным недостатком ДИКМ является то, что ошибки, возникающие в кодовых комбинациях при передаче, ухудшают верность приема в большей степени, чем при обычной ИКМ. Это объясняется тем, что ошибочный прием кодовой комбинации при ДИКМ ведет к ошибочному восстановлению не только одного отсчета, но и ряда последующих отсчетов, поскольку предсказанные значения на приемной стороне будут отличаться от предсказанных на передающей. Поэтому допустимая вероятность ошибки при ДИКМ меньше, чем при ИКМ.

Существуют различные методы уменьшения влияния указанного накопления ошибки при ДИКМ.

Разновидность способа с предсказанием, когда кодируется и передается информация только о знаке приращения разности за интервал дискретизации, называют дельта- модуляцией (ДМ).

Идея, положенная в основу ДМ, состоит в следующем. Величина разностного сигнала Da зависит от корреляции между значениями отсчетов, сдвинутых на интервал дискретизации. По мере уменьшения интервала дискретизации корреляция между отсчетами увеличивается, а величина Da уменьшается. Если выбрать интервал дискретизации настолько малым, что Da не будет превышать одного шага квантования d, то передачу разностного сигнала можно осуществить, используя одноразрядный код. Если, например, окажется, что Da>0, то кодирующее устройство формирует символ «1», а если Da<0, то символ «0». Получающаяся при этом двоичная последовательность называется дельта -кодом.

Для того, чтобы величина разностного сигнала не превышала шага квантования, частота дискретизации при ДМ должна выбираться значительно большей, чем при ДИКМ. Тем не менее, для ДМ, как и для ДИКМ, возможно возникновение перегрузки по крутизне, если величина разностного сигнала окажется больше шага квантования

Выбор величины шага квантования подчиняется противоречивым требованиям. С одной стороны, шаг квантования следует выбирать как можно меньшим, чтобы уменьшить шум квантования до допустимого значения. С другой стороны, при заданной частоте дискретизации шаг квантования следует выбирать достаточно большим, чтобы не возникло перегрузки по крутизне. Если оставлять шаг квантования постоянным, то удовлетворить этим требованиям удается только при частоте дискретизации в 2-3 раза превышающей частоту дискретизации ИКМ- сигнала при тех же шумах квантования. Снизить частоту дискретизации без увеличения шумов квантования возможно при использовании адаптивной ДМ, когда шаг квантования в процессе модуляции не остается постоянным, а изменяется в зависимости от параметров модулируемого сигнала.

При ДМ ошибки в линейном тракте вызывают ошибку в выходном сигнале, не превосходящую двух шагов квантования. При ИКМ ошибка в наихудшем случае составляет 2^m-1 уровней квантования, где m- число разрядов в кодовой комбинации. Этим определяется, что требования к линейному тракту по достоверности передачи при ДМ на несколько порядков ниже, чем при ИКМ.

При ИКМ для демодуляции сигнала требуется два вида синхронизации: тактовая (по битам) и по кодовым комбинациям. При ДМ принципиально отсутствуют кодовые комбинации, и требуется только синхронизация по тактам.

Рассмотренное описание цифровых методов модуляции показывает их глубокое единство. Наиболее общий метод – ИКМ с предсказанием. Частными случаями являются ДИКМ и ДМ. Метод ИКМ можно рассматривать как ИКМ с предсказанием, при которой предсказанное значение на каждом такте принимается равным нулю, а кодируются независимые отсчеты сигнала. В случае ИКМ перегрузка по крутизне имеет ту же природу и возникает, если отсчеты сигнала выходят за пределы шкалы квантования. Такое единство методов цифровой модуляции позволяет производить их анализ и сравнение с общих позиций.