Порог чувствительности.

Невозможно увеличивать чувствительность ИС до бесконечности (например, путем увеличения коэфф. усиления): идя по этому пути, мы столкнемся с порогом чувствительности—наименьшим входным сигналом, который все еще обнаруживается с заданной вероятностью правильного решения. Предельное значение порога чувствительности обусловлено шумами в ИС. В этом случае порог чувствительности определяется вероятностными методами: общепринятой мерой порога чувствительности является величина входного сигнала, для которого отношение сигнал/шум равно единице, т.е. 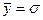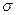выборочное значение сигнала , где -среднеквадратическое значение шума на выходе ИС. Тогда, в случае шума с нормальным распределением мгновенных значений, вероятность обнаружения оказывается равной примерно 70%.

Вероятность обнаружения при разных отношениях сигнал/шум

Сигнал 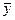Вероятность обнаружения сигнал/шум ( )

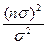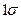69.15% 1

1.4 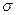76.11% 2

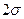84.13% 4

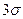93.32% 9

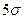99.38% 25

В этом случае выносится решение о наличии сигнала по одному выборочному измерению. Порог чувствительности улучшается, когда мы выносим решение на основании n выборок .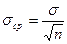

Отношение сигнал/шум в данном случае составляет .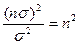

Порог чувствительности можно также улучшить , сужая ширину полосы 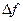измерительной системы. Полагая, что шум белый, получаем:

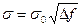, где 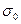-эквивалентный шум в полосе 1Гц.

В качестве альтернативы нахождения среднего от n отдельных последовательных выборок мы можем также измерять входной сигнал непрерывно в течении определенного интервала времени Т:

.

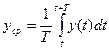Применим теорему Котельникова о выборках (если у сигнала y(t) нет составляющих на частотах выше, чем 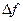Гц , то этот сигнал полностью определяется выборками, взятыми с интервалом 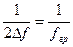на отрезке времени Т, много большем чем 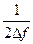). Число дискретных выборок, описывающих 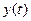на отрезке Т секунд, равно 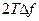. Возьмем среднее от этих 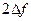выборок. Среднеквадратическое значение шума в сигнале будет равным .

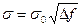В этом случае: ,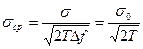

Т.обр. порог чувствительности снижается в 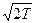раз.

Эти меры требуют затраты большего времени для получения результата; как следствие отклик измерительной системы становится более медленным (за все надо платить!)