Просторове та косе згинання

Згинання називають просторовим, якщо усі навантаження діють у декількох площинах, які перетинаються на поздовжній осі балки (рис. 1.4 а).

Згинання називають косим, якщо усі навантаження діють у одній (силовій) площині, яка перетинає вісь балки , але не включає жодної з головних центральних осей інерції перерізу.

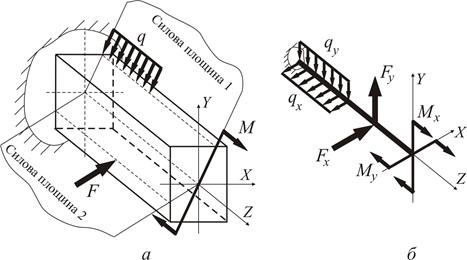
Рисунок 1.4

Розрахунки балок, які знаходяться в умовах косого або складного згинання, можна звести до сумісної дії двох плоских згинань у головних площинах. Для цього навантаження, що діють у довільних силових площинах треба проецирувати до головних площин 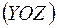, 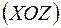(рис. 1.4 б). Таким чином, у будь-якому перерізі балки виникають чотири внутрішні силові фактори: .

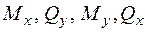Треба зазначити, що в даному методичному посібнику ми свідомо не торкаємося питань згинання тонкостінних відкритих профілів ( з однією віссю симетрії або без неї) , для яких поперечні сили, що проходять крізь центр ваги перерізу, породжують систему неврівноважених дотичних напружень. Останні утворюють крутний момент 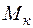, що зумовлює вільне або стиснуте кручення.

У практичних розрахунках на міцність для більшості перерізів малими дотичними напруженнями 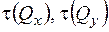, як правило нехтують. Таким чином, враховують лише нормальні напруження від дії згинальних моментів .

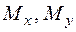Незважаючи на загальні підходи до рішення задач косого і складного згинання, є деякі відмінності у цих випадках складного опору:

а) при косому згинанні деформована вісь бруса є плоскою кривою, а при складному згинанні – просторовою;

б) згинальні моменти 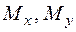у випадку косого згинання набувають максимальних значень в одному перерізі, а якщо згинання складне, − здебільшого в різних.

Розглянемо жорстко затиснуту консольну балку, навантажену на вільному кінці силою 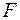, яка лежить у силовій площині, нахиленій під кутом 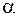до головної площини 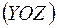(рис. 1.5 а).

Розкладемо зусилля 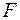по головних осях перерізу і, таким чином, зведемо задачу косого згинання до комбінації двох плоских згинань у головних площинах 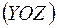та .

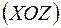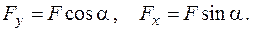
У довільному перерізі 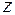згинальні моменти визначаються за співвідношеннями:

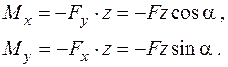(1.2.1)

Максимальні значення вони набувають у перерізі 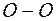, при 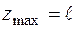, який є найбільш небезпечним.

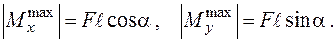
Обчислимо напруження в точці 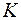довільного перерізу, яка знаходиться у першому його квадранті (рис. 1.5 б) [1]:

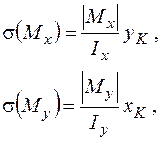
де 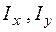− осьові моменти інерції перерізу.

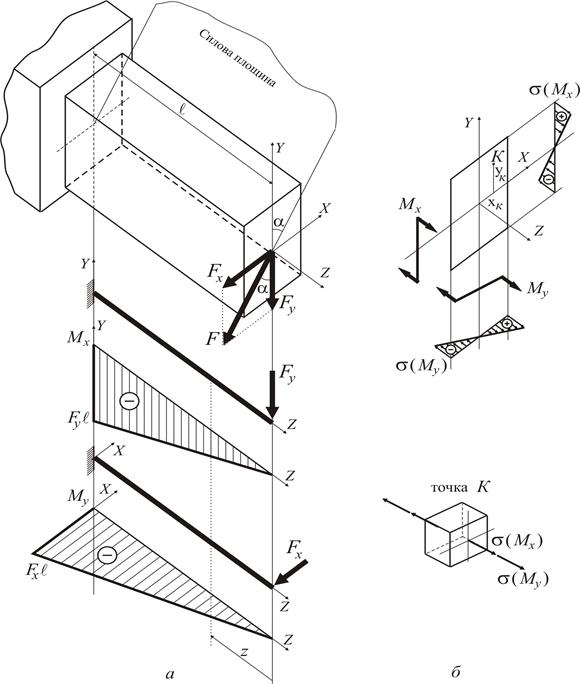
Рисунок 1.5

Оскільки тип напружень від дії згинальних моментів 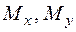однаковий (рис. 1.5 б) , їх можна алгебраїчно просумувати:

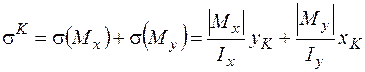. (1.2.2)

Усі складові співвідношень (1.2.2) (згинальні моменти та координати) будемо вважати додатними, а знак приписувати кожному сполучнику окремо, зважаючи на деформації у відповідному квадранті.

Аналізуючи розподіл нормальних напружень у перерізі (рис. 1.5 б), робимо висновок, що нульові напруження можуть знаходиться лише у точках другого та четвертого квадрантів.

Позначимо через 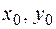(рис. 1.6) координати точки, яка належить нейтральній лінії (де нормальні напруження 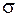дорівнюють нулю), тоді з формули (1.2.2) маємо:

.

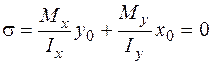Це рівняння є рівнянням прямої, що проходить крізь початок координат (центр ваги перерізу). Кутовий коефіцієнт цієї прямої:

.

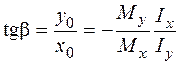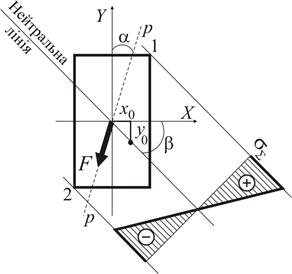
Рисунок 1.6

Якщо зважити, що з формул (1.2.1)

,

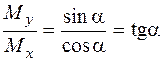то остаточно

.

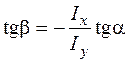Таким чином, нейтральна лінія завжди відхиляється від осі 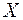на кут 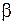в ту ж сторону, в яку слід силової площини відхиляється від осі 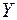на кут 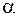(рис. 1.6). Різниця між цими кутами залежить від співвідношення осьових моментів інерції перерізу. Наприклад, якщо прийняти 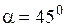, а співвідношення 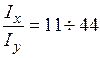(що відповідає двотавру), легко підрахувати кут 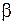, який коливається між 85÷89 градусами.

То ж у випадку косого або просторового згинання для перерізів при 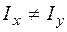нейтральна лінія не є ортогональною до сліду площини 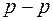дії згинального моменту. Ця обставина є характерною рисою косого згинання. І навпаки, якщо головні моменти інерції однакові ( 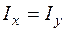), косе згинання унеможливлюється, бо кути 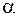і 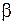стають рівними, тобто нейтральна лінія стає ортогональною до сліду силової площини, а це є ознакою прямого згинання. Так відбувається у разі, якщо переріз балки є кругом, кільцем, квадратом і т.п.

Для визначення найбільш небезпечних точок ( у розтягнутій та стислій зонах) у випадку довільного перерізу проведемо дві паралельні до нейтральної лінії прямі, які дотичні до контурних точок перерізу. У створі між цими прямими будується епюра сумарних нормальних напружень.

Точки 1 та 2 є найбільш віддаленими від нейтральної лінії і тому найбільш напруженими (рис. 1.6). У нашому прикладі в точці 1 діють максимальні розтягуючі, а у точці 2 – стискаючі напруження.

Таким чином, умови міцності для перерізу мають вигляд:

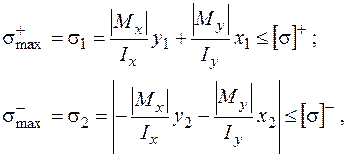(1.2.3)

де 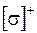та 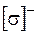– допустимі напруження розтягання та стискання відповідно.

Якщо переріз має дві вісі симетрії та кутові точки контуру, наприклад, прямокутник, то співвідношення (1.2.3) дещо скорочуються:

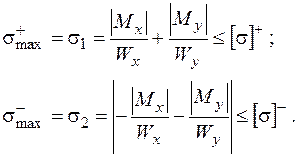(1.2.4)

В цих виразах

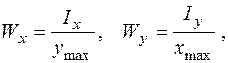(1.2.5)

− осьові моменти опору, а 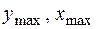– координати найбільш віддалених від нейтральної лінії точок.

У випадку, якщо матеріал стержня має однакову міцність на розтягання і стискання, тобто 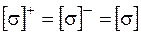, то умови (1.2.4) перетворюються:

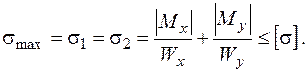(1.2.6)

Зрозуміло, що найбільші напруження будуть спостерігатись у найбільш небезпечних перерізах, де згинальні моменти набувають своїх максимальних значень.

Відносно складових напруження 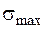у виразах (1.2.4) та (1.2.5) можна зробити наступні спостереження. У перерізах, де 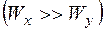, що опиняються в умовах косого або просторового згинання, можна говорити про наявність «сильної» 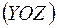та «слабкої» 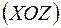площин перерізу. Тому дія малого згинального моменту у «слабкому» напрямку може привести до появи більших напружень, ніж при дії значного моменту у «сильній» площині.

Доречи, якщо переріз балки має виступаючі кути і може бути вписаний в прямокутник, то незалежно від положення нейтральної лінії найбільш віддаленими точками будуть відповідні кутові. У таких випадках, для розрахунків максимальних напружень у перерізі визначення положення нейтральної лінії втрачає сенс.

Добір перерізів при косому та просторовому згинанні – задача більш складна, ніж при прямому плоскому згинанні. При її розв’язанні треба задатися відношенням моментів опору:

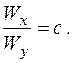(1.2.7)

Тоді, з урахуванням (1.2.7), умова міцності (1.2.4) буде мати вигляд:

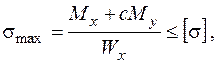
а моменти опору визначаються наступним чином:

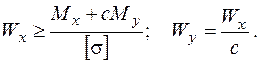
У випадку просторового згинання, якщо згинальні моменти набувають максимальних значень у двох різних перерізах, задача вирішується за допомогою метода спроб з послідуючою перевіркою. Перша спроба виконується у перерізі, де діє максимальний за абсолютною величиною момент. У іншому (другому) перерізі обов’язково виконується перевірка.