Представление синусоидальных функций с помощью векторов

<4 5 6 789 10 >

При гармоническом изменении синусоидальной величины постоянной остается амплитуда. Этим можно воспользоваться для определения мгновенного значения электрической величины, не рассматривая графика ее зависимости от времени.

►Синусоидальную функцию времени можно изобразить вектором, равным амплитуде данной функции, равномерно вращающимся с угловой скоростью 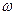. При этом начальное положение вектора определяется (для t = 0) его начальной фазой 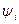. На рис. 25 показаны вращающийся вектор тока 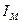(рис.25, а) и график изменения тока i во времени (рис.25, б).

ЗАПОМНИТЕ

При изображении синусоидальных эдс, напряжений и токов из начала координат

проводят векторы, равные амплитудным значениям этих величин, под углом |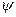

к горизонтальной оси. Положительные углы 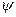откладываются против часовой стрелки. Если вращать вектор против часовой стрелки, то в любой момент времени он составит с горизонтальной осью угол, равный 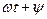.Проекция вращающегося вектора на ось ординат (ось мгновенных значений) равна мгновенному значению синусоидальной величины (эдс, напряжения, тока).

Совокупность векторов на плоскости, изображающих эдс, напряжения и токи одной частоты, называют векторной диаграммой.

При исследовании установившихся режимов векторы неподвижны, их длина равна действующим значениям электрических величин.

С помощью векторов можно производить геометрическое суммирование электрических величин. Так, на рис. 25, в показаны

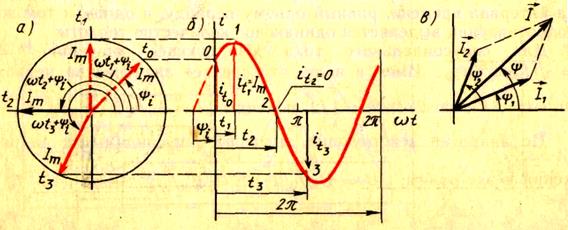
векторы токов 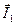и 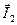, а также вектор их геометрической суммы 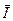= 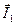+ 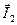_. Углы 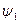, , 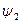и 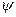обозначают начальные фазы токов.

Векторные диаграммы широко используют при анализе электрических цепей переменного тока.

<4 5 6 789 10 >

Дата добавления: 2020-10-14; просмотров: 344;