Устройство резистора

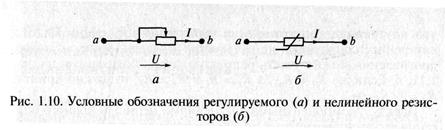
Условное обозначение резисторов на схеме (нерегулируемый и регулируемый);

Противодействие проводника направленному движению зарядов (электрическому току) называется сопротивлением проводника.

Устройство обладающее сопротивлением и используемое для ограничения силы тока в эл. цепи или приемнике эл. энергии называется резистором. Регулируемый резистор, включенный в электрическую цепь тока, называется реостатом.

Наряду с сопротивлением R резистор иногда характеризуют обратной величиной G = 1/R называемой проводимостью. Единицей прово­димости является сименс (1 См = 1 А/1 В). На схемах указывается одна из этих величин — сопротивление R или проводимость G. Введе­ние проводимости иногда упрощает преобра­зования уравнений цепи, содержащей не­сколько резисторов.

Сопротивлением R можно охарактеризовать любой проводник длиной l и площадью сечения S (рис. 1.3). Если ток распределен по сечению проводника равномерно,

то 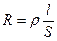,— , где 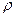— удельное электрическое сопротивление, характеризующее свойства мате­риала проводника.

Единицей удельного электрического сопротивления является Ом, умноженный на метр (Ом • м). В схеме замещения электричес­кой цепи резистивные элементы отражают не только резисторы, но и сопротивления проводов линий электропередачи, сопротив­ления проводников, из которых выполнены обмотки трансфор­маторов и электрических машин, и т.п.

Удельное электрическое сопротивление некоторых проводников при температуре 20 °С, мкОм • м, составляет:

Серебро.................................................................................... 0,016

Медь....................::................................................................... 0,0175

Алюминий ............................................................................... 0,029

Вольфрам................................................................................. 0,056

Сталь........................................................................................ 0,13...25

Константан, манганин .......................................................... 0,4...0,5

Нихром .................................................................................... 1,1

Конструктивно резисторы различных по номиналу и помощности а так же их назначения и могут сильно отличаться. Общим является использование в их конструкциях материалов с большим сопротивлением — константана, манганина и др.

Наряду с рассмотренными силовыми элементами в состав цепи могут входить также измерительные приборы, такие как амперметры (обозначаются буквой А в кру­жочке) для измерения токов и вольтметры (обозначаются бук­вой V в кружочке) для измерения напряжения. На рис. 1.11, а показана схема, содержащая один амперметр (для измерения тока i₁) и один вольтметр (для измерения напряжения u₂= u₃). При правильном включении этих приборов не происходит из­менения режима (т.е. не изменяются или почти не изменяются токи и напряжения элементов цепи). Это достигается за счет того, что внутреннее сопротивление амперметра R_А очень мало, а внутреннее сопротивление вольтметра очень велико. Если же R_А << R_ВН , а R_В >> R₃ , то можно принять R_А=0, R_В = ∞,

Законы Кирхгофа

Наряду с компонентными уравнениями цепи для полного опи­сания ее электромагнитных процессов применяют два закона Кирх­гофа.

Для любого узла справедлив первый закон Кирхгофа: алгебра­ическая сумма токов ветвей, соединенных с данным узлом, равна нулю. При этом ток, исходящий из узла, берется со знаком «плюс», а подходящий к узлу — со знаком «минус». Для узла I, изображен­ного на рис. 1.11, б, имеем

-I₁ + I ₂ + I ₃ + 1_V = 0.

Для любого контура (замкнутого пути, проходящего через не­сколько элементов) справедлив второй закон Кирхгофа: алгебраи­ческая сумма напряжений на всех элементах контура равна нулю. Для практического использования этого закона необходимо за­дать определенные направления обхода контура, тогда напряже­ния элементов, совпадающие с направлением обхода, берутся со знаком «плюс», не совпадающие — со знаком «минус». Для одно­контурной схемы, изображенной на рис. 1.6, б, при обходе конту­ра по часовой стрелке имеем -U+ U₁ + U_Н = 0.

В общем случае, если число ветвей цепи равно В, а число узлов — У, то число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно У - 1 , а по второ­му:

В - (У-1) = В -У+1. Таким образом, всего по законам Кир­хгофа можно составить В уравнений. Дополнив эти В уравнения В-компонентными уравнениями, получим 2В уравнений, необ­ходимых для определения В токов и В напряжений рассматривае­мой схемы. Эти 2В уравнений называют полной системой уравне­ний схемы электрической цепи. Они позволяют решить задачу расчета (анализа) цепи — по заданной схеме и значениям пара­метров рассчитать неизвестные токи и напряжения ветвей.

Для решения подобных сложных задач анализа разработаны спе­циальные методы, которые будут рассмотрены далее.