ЛАБОРАТОРНАЯ РАБОТА 8

БИНАРНОЕ УПОРЯДОЧЕННОЕ ДЕРЕВО

Введение

Дерево является нелинейной динамической структурой хранения данных. Дерево состоит из узлов или вершин, которые содержат поля данных и указатели на другие узлы или вершины.

Бинарное дерево

Узел или вершина бинарного дерева содержит поле данных и два поля с указателями. Поля указателей называются левым указателем (left) и правым указателем (right), поскольку они указывают на левое и правое поддерево, соответственно. Значение NULL указателя является признаком пустого поддерева.

Корневой узел определяет входную точку дерева, а поле указателя – узел следующего уровня. Листовой узел (лист) содержит NULL в поле правого и левого указателей.

Класс TreeNode

Объекты класса TreeNode являются узлами бинарного дерева (рис.8.1).

class TreeNode

{

private:

// указатели левого и правого дочерних узлов

TreeNode* left;

TreeNode* right;

public:

// открытый элемент

int data;

// конструктор

TreeNode(const int& item, TreeNode* lptr=NULL,

TreeNode* rptr=NULL);

// функции-элементы доступа к полям указателей

TreeNode* Left() const;

TreeNode* Right() const;

};

Конструктор инициализирует поля данных и указателей. С помощью пустого указателя NULL узлы инициализируются как листья. Имея указатель P объекта класса TreeNode в качестве параметра, конструктор присоединяет P как левого или правого потомка нового узла. Функции-элементы Left() и Right() возвращают значения полей левого и правого указателей. Благодаря этому клиент класса имеет доступ к левому и правому потомкам узла.

Примеры

// указатели целочисленных узлов дерева

TreeNode*root, *lp, *rp;

TreeNode*p;

// создать листья, содержащие 20 и 30 в качестве данных

lp=new TreeNode (20);

rp=new TreeNode (30);

// создать корень, содержащий число 10 и двух потомков

root= new TreeNode (10, lp, rp);

Рис.8.1 – бинарное дерево

root->data=50;// присвоить корню 50

Переопределение конструктора

// конструктор инициализирует поля данных и указателей

// значение NULL соответствует пустому поддереву

TreeNode:: TreeNode (const int& item, TreeNode*lp,

TreeNode*rp):data(item), left(lp), right(rp)

{}

Бинарное упорядоченное дерево ( дерево поиска)

Бинарное дерево поиска – это структура (рис.8.2), которая упорядочивает элементы посредством отношения “<”. Чтобы сравнить узлы дерева, подразумевают, что часть или все поле данных определено в качестве ключа и операция “<” сравнивает ключи при размещении элемента на дереве.

Бинарное дерево поиска строится по следующему правилу:

Для каждого узла значения данных в левом поддереве меньше, чем в этом узле, а в правом поддереве – больше.

Дерево называется поисковым потому, что в поисках некоторого элемента (ключа) можно идти лишь по совершенно конкретному пути. Начав с корня, сканируют левое поддерево, если значение ключа меньше текущего узла. В противном случае сканируют правое поддерево. Метод создания дерева позволяет осуществлять поиск по кратчайшему пути от корня. Бинарные деревья поиска предназначены для быстрого доступа к данным. В идеале дерево является сбалансированным и имеет высоту и эффективность поиска порядка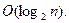

Рис.8.2 – бинарное упорядоченное дерево

Для обработки данных, размещенных в дереве, применяют следующие методы прохождения дерева:

левое поддерево-узел-правое поддерево, или симметричный метод;

левое поддерево-правое поддерево-узел, или обратный метод;

правое поддерево-узел- левое поддерево, или справа-налево;

узел-левое поддерево-правое поддерево, или сверху-вниз.

Для реализации методов используют рекурсивные алгоритмы.

Класс BinSTree

Объектом этого класса является бинарное упорядоченное дерево (пример - на рис.8.2).

// класс - бинарное дерево

class BinSTree

{

public:

// конструкторы и деструктор

BinSTree();

//конструктор копирования

BinSTree(const BinSTree& tree);

~BinSTree();

// оператор присваивания

BinSTree& operator=(const BinSTree& rhs);

// функции-элементы обработки данных

int Find(int& item); // есть или нет узла с item

void Insert(const int& item); // вставить узел с item

void Delete(const int& item); // удалить узел с item

void ClearTree(); // уничтожить дерево

TreeNode *CopyTree(TreeNode *t); // копировать дерево

int Depth(TreeNode *t); // получить глубину дерева

// получить количество листьев в дереве

void CountLeaf(TreeNode *t,int& count);

// получить корень дерева

TreeNode *GetRoot() const {return root;}

// получить количество узлов в дереве

int GetSize() const {return size;}

private:

// указатель на корень

TreeNode *root;

// количество узлов в дереве

int size;

// выделить память под узел дерева

TreeNode *GetTreeNode(const int& item,

TreeNode *lptr, TreeNode *rptr);

// удалить все узлы дерева

void DeleteTree(TreeNode* t);

// получить указатели - на узел с item и его родителя

TreeNode *FindNode(const int& item,

TreeNode* &parent)const;

};

Конструктор инициализирует данные-элементы. Конструктор копирования и перегруженный оператор присваивания с помощью функции-элемента CopyTree создают новое бинарное дерево для текущего объекта.

Алгоритм удаления узлов дерева реализован функцией-элементом DeleteTree и используется функцией-элементом ClearTree, вызываемой как деструктором, так и перегруженной операцией присваивания.

Функции-элементы Find и Insert начинают с корня и используют определение бинарного дерева поиска. Алгоритм идет по правому поддереву, когда ключ или новый элемент больше значения текущего узла. В противном случае прохождение продолжается по левому поддереву. Функция-элемент Find использует закрытую функцию-элемент FindNode, принимающую в качестве параметра ключ и осуществляющую прохождение вниз по дереву. Функция возвращает указатель на совпавший узел и указатель на его родителя. Если совпадение происходит в корне, родительский указатель равен NULL.

Функция-элемент Delete удаляет из дерева узел с заданным ключом. Сначала с помощью функции-элемента FindNode устанавливается место этого узла на дереве и определяется указатель на его родителя. Если искомый узел отсутствует, операция удаления завершается.

Удаление узла из дерева требует ряда проверок, чтобы определить, куда присоединить сыновей удаляемого узла. Поддеревья должны быть заново присоединены таким образом, чтобы сохранилась структура бинарного упорядоченного дерева.

Функция FindNode возвращает указатель DNodePtr на узел D, подлежащий удалению. Второй указатель, PNodePtr, идентифицирует узел P – родителя удаляемого узла. Функция Delete ”пытается” подыскать заменяющий узел R, который будет присоединен к родителю и, следовательно, займет место удаленного узла. Заменяющий узел R идентифицируется указателем RNodePtr.

Функция Delete реализует алгоритм поиска заменяющего узла из четырех случаев, зависящих от числа и расположения сыновей удаляемого узла. Отметим, что если указатель на родителя равен NULL, то удаляется и обновляется корень. Эта ситуация учитывается алгоритмом.

Чтобы функции-элементы класса BinSTree получили доступ к закрытым данным-элементам left и right класса TreeNode, класс BinSTree объявляется другом класса TreeNode. Это объявление предваряется формальным объявлением класса BinSTree.

Целью данной лабораторной работы является изучение алгоритмов и функций работы с бинарным упорядоченным деревом на примере дерева из целых чисел.