УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКОЙ ДУГИ ПОСТОЯННОГО ТОКА

Чтобы погаситьэлектрическую дугу постоянного тока, необходимо создать условия, при которых в дуговом промежутке процессы деионизации превосходили бы процессы ионизации при всех значениях тока.

Для цепи (рис. 3), содержащей сопротивление R, индуктивность L, дуговой промежуток с падением напряжения Uд, источник постоянного тока напряжением U, в переходном режиме ( ) справедливо уравнение Кирхгофа: 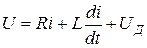, (1) где – падение напряжения на ин­дуктивности при изменении тока. При устойчиво горящей дуге (стационарное состояние 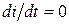) выражение (1) принимает вид: . (2) Для погасания дуги необходимо, чтобы ток в ней все время уменьшался. Это означает, что : 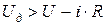. (3) Графическое решение уравнения (3) приведено на рис. 4. Прямая 1 – напряжение источника U, прямая 2 – падение напряжения в сопротивлении (реостатная характеристика), кри­вая 3 – ВАХ дугового промежутка Uд.

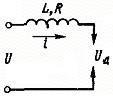Рис. 3 Рис. 4 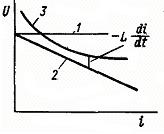Рис. 5

В точках а и б справедливо уравнение (2), значит 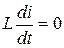. Здесь имеет место равновесное состояние. В точке а равновесие неустой­чивое, в точке б устойчивое.

При токах , напряжение 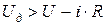, a , и если по какой-либо причине ток станет меньше I_{а ,} то он упадет до нуля – дуга погаснет.

Если же по какой-либо причине ток станет несколько больше I_а, то будет , в цепи как бы окажется «избыточное» напряжение, которое приведет к возрастанию тока до значения I_б. При любом значении I_а < i < I_б ток в дуге будет возрастать до значения I_б.

Между точками а и б величина 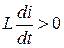. Рост тока в цепи сопровождается накоплением электромагнитной энергии.

При токе 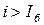снова оказывается 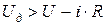, а , т. е. для поддержания такого значения тока напряжение U недоста­точно. Ток в цепи будет падать до значения I_б. Дуга в этой точке будет гореть устойчиво.

Для погасания дуги необходимо, чтобы при любом значении тока соблю­далось условие (3), то есть ВАХ дуги должна лежать выше характеристики (рис. 5) на всем своем протяжении и не иметь с этой характеристикой ни одной точки соприкосновения.