Определительные испытания

Определительным испытаниям могут подвергаться АСУ ТП в целом, их подсистемы, функции, технические средства и любые другие элементы АСУ ТП.

Планы испытаний.Планом испытаний называют правила, устанавли­вающие объем выборки, порядок проведения испытаний и критерии их пре­кращения. Рассмотрим наиболее распространенные планы определительных испытаний. Наименование плана принято обозначать тремя буквами (цифра­ми); первая из них обозначает число испытываемых систем, вторая – нали­чие R или отсутствие U восстановлений на время испытаний в случае отказа, третья – критерий прекращения испытаний.

План [N U 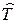] соответствует одновременному испытанию N систем. Эти сис­темы после отказа не восстанавливаются (или же восстанавливаются, но данные об их поведении после первого отказа в испытаниях не рассматрива­ются). Испытания прекращают по истечении наработки каждой отказавшей системы. На рис. 4.1,а знаком умножения обозначено наличие отказа; 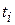– наработка до отказа 1-й системы. Этот план обычно применяют для опреде­ления вероятности безотказной работы системы за время .

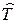План [N U r] соответствует испытаниям N таких же невосстанавливаемых систем, однако в отличие от плана [N U 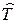] испытания прекращают, когда чис­ло отказавших систем достигает r. В примере плана, данного на рис. 4.1,б, r-й отказ имеет место у 1-й системы. Если r = N, то переходим к плану [N U N], когда испытания прекращают после отказов всех систем.

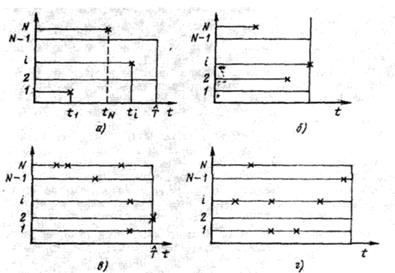
Рис. 4.1 Планы испытаний

План [N U r]обычно применяют для определения средней наработки на отказ и средней наработки до отказа в случае экспоненциального распределе­ния, а план [N U N] – в случае нормального распределения. Испытания по плану [N U N] требуют значительных времени и числа испытываемых систем, но дают возможность полностью определить эмпирическую функцию рас­пределения. Планы [N U r] и [N U 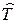] позволяют определить эмпирическую функцию распределения только для некоторого интервала времени, дают меньше информации, зато позволяют быстрее закончить испытания.

План [N R 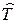] описывает испытания N систем, причем отказавшие во вре­мя испытаний системы заменяют новыми или восстанавливают. Испытания прекращают по истечении наработки Т каждой из N позиций (под позицией понимаем определенное место на стенде или объекте, применительно к кото­рому наработка исчисляется независимо от произошедших на данной пози­ции замен или восстановлений – рис. 4.1,в).

Последний из рассматриваемых планов [N R r] соответствует испытаниям N систем, когда отказавшие во время испытаний системы заменяют новыми или восстанавливают. Испытания прекращают, когда суммарное по всем по­зициям число отказавших систем достигает r (рис. 4.1,г).

Задачами планирования является определение минимального объема на­блюдений – выбор числа испытываемых систем N, а также продолжительно­сти наблюдений 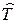для планов [N U 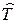] и [N R 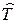] или числа отказов r для планов [N U r] и [N R r].

Результатами определительных испытаний должны являться точечные и интервальные оценки показателей надежности.

Точечные оценки.Понятие точечная оценка в математической статисти­ке вводится следующим образом. Пусть имеются результаты k наблюдений t₁, t₂ ,..., t_k над некоторой случайной величиной T (например, временем безот­казной работы) с функцией распределения F (t, ), причем параметр этого распределения неизвестен. Необходимо найти такую функцию =g(t₁,..., t_k)результатов наблюдений t₁,..., t_k, которую можно было бы рассматривать как оценку параметра . При таком выборе функции каждой совокупности (t₁,..., t_k)будет соответствовать точка на числовой оси, которую называют точечной оценкой параметра .

Точечная оценка 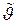, являющаяся функцией результатов наблюдений, – так же случайная величина со своим собственным законом распределения, зависящим от закона распределения случайной величины T, объема наблюдений k и вида функции . Для одного и того же неизвестного параметра обычно можно принять несколько функций , которые могут служить в качестве оценки. Выбор требований к таким оценкам (состоятельности, несмещенно­сти, эффективности) и методов нахождения оценки (максимального правдоподобия, моментов, квантилей, графические) описан в книгах по теории веро­ятностей и математической статистике.

Статистические определения показателей надежности, рассмотренные ранее являются их точечными оценками. При этом оценка средней наработки до отказа

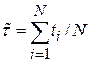(4.1)

соответствует плану [N U N], так как здесь рассматриваются завершенные (не прерванные в испытаниях) наработки до отказа каждой из испытываемых систем. Это соотношение имеет место при любых законах распределения наработки до отказа.

Для экспоненциального распределения при всех других рассмотренных в п. 4.1 планах испытаний, кроме плана [N U N], точечная оценка средней на­работки до отказа

,

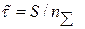где S – суммарная наработка всех систем за время испытаний;

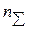– cуммарное числе отказов всех систем за время испытания. Например, при плане [N R ]

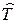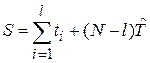, (4.2)

где l – число систем, отказавших в интервале (0, 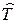); t_i – наработка до от­каза l-й системы из числа отказавших (i = 1, 1).

При плане испытаний [N U r]

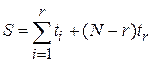. (4.3)

Для плана [N R 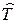]и простейшего потока, у которого время между отка­зами подчиняется экспоненциальному распределению, оценка 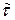средней наработки до отказа совпадает с оценкой 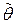средней наработки на отказ:

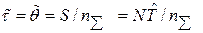. (4.4)

Оценка интенсивности отказов 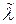при экспоненциальном распределении может быть определена через оценку средней наработки до отказа:

.

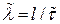Например, при плане [N U N]

.

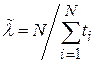Оценка параметра 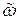простейшего потока совпадает с оценкой интенсивности отказов 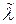. Например, при плане [N R ]:

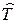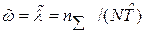. (4.5)

Оценка среднего времени восстановления, определяемая аналогично (4.1), также соответствует плану [N U N]. Оценки вероятности отказа 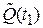и вероятности безотказной работы 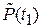до момента t₁, определяемые соотно­шениями (1.8) и (1.9), могут быть найдены за ограниченный интервал време­ни t₁= 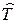и соответствуют плану испытаний [N U ].

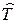ЛЕКЦИЯ 11