Интервальные оценки

Точечные оценки дают представление о значе­нии показателя надежности, но ничего не говорят о точности этой оценки. Для рассмотрения точности оценки вводится понятие доверительного ин­тервала.

Как выше, примем, что имеются результаты k наблюдений t₁,..., t_k над случайной величиной Т с функцией распределения F(t, ), где параметр неизвестен. Необходимо найти такую функцию 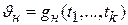результатов наблюдений, чтобы интервал ( _н, ∞) накрывал неизвестный параметр с заданной вероятностью :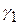

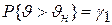. (4.6)

Величину _н называют нижней доверительной границей параметра при односторонней доверительной вероятности .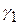

Для заданной вероятности 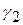по той же совокупности наблюдений может быть найдена функция 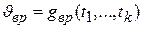такая, что интервал (0, _вр) накрывает параметр с вероятностью :

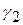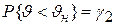. (4.7)

Величину _вр называют верхней доверительной границей параметра при односторонней доверительной вероятности .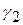

Нижняя и верхняя доверительные границы образуют доверительный ин­тервал, который с вероятностью 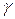накрывает на числовой оси неизвестное значение параметра . При 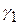>0,5 и 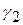>0,5(доверительные вероятност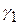и и 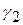обычно выбираются не менее 0,8) согласно (4.7) и (4.8):

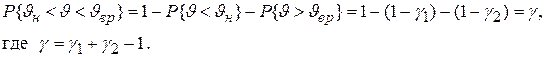
Обычно принимают, что 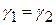, тогда .

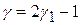Значение доверительного интервала тем меньше, чем больше число k на­блюдений (например, чем больше число отказов при испытаниях) и чем меньше значение 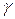доверительной вероятности.

Определение границ доверительного интервала заключается в следующем. Так как оценка 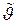неизвестного параметра является случайной величиной, то находим закон ее распределения. Затем определяем интервал 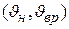,в который случайная величина 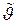попадает с вероятностью .

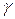С помощью (4.11) может быть получен приближенный способ построения доверительных интервалов средней наработки до отказа для плана [N U N] при произвольном распределении. Способ основывается на том, что незави­симо от исходного распределения уже при числе испытываемых изделий N >15 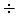20 среднее арифметическое, т.е. оценка 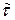, распределено приближенно нормально с математическим ожиданием 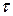, а неизвестное значение диспер­сии заменяется ее точечной оценкой такой же, как в соотношении (4.6):

.

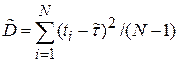Тогда, как в предыдущем случае, получим относительные значения границ доверительного интервала.