Синусоидальный ток в емкости
| Система из двух проводящих тел, разделенных диэлектриком, образует конденсатор. Эти проводящие тела называются обкладками. Если к ним подключить источник энергии, то на них будет накапливаться заряд q, пропорциональный напряжению на конденсаторе uC (рис. 2.21): |  Рис. 2.21. Обозначение конденсатора
Рис. 2.21. Обозначение конденсатора
|
q = CuC.. (2.19)
Коэффициент пропорциональности C между зарядом и напряжением называется емкостью конденсатора. Единица измерения емкости – фарад (Ф). Она имеет следующую размерность: 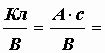
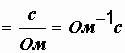 . Емкость зависит от формы, размеров конденсатора и от диэлектрической проницаемости диэлектрика между обкладками.
. Емкость зависит от формы, размеров конденсатора и от диэлектрической проницаемости диэлектрика между обкладками.
Пусть напряжение, подаваемое источником на конденсатор, изменяется по закону
uC = UCm sin (w t+y ). (2.20)
При его возрастании от нуля до максимального значения конденсатор заряжается, на его обкладки от источника поступает электрический заряд. При уменьшении напряжения от максимума до нуля, заряд стекает с конденсатора, он разряжается. Таким образом, в проводах, соединяющих конденсатор с остальной цепью, постоянно движется электрический заряд, т.е. протекает электрический ток. Вывод о наличии электрического тока мы делаем, совершенно не касаясь вопроса о том, какие процессы происходят между обкладками конденсатора. Величина тока определяется зарядом, прошедшим в единицу времени через поперечное сечение проводника:
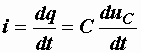 . (2.21)
. (2.21)
Она зависит от емкости и скорости изменения питающего напряжения, т.е. от частоты. От этих же факторов зависит и электрическая проводимость участка цепи с конденсатором. Ее называют емкостной проводимостью и определяют по формуле
BC = w C = 2p fC.
Величина, обратная емкостной проводимости, называется емкостным сопротивлением:
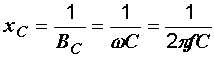 .
.
Подставляя в (2.21) приложенное к конденсатору напряжение из (2.20), получаем
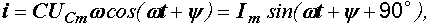 (2.22)
(2.22)
где Im = w CUCm = BcUCm.
Действующее значение тока
I = w CUC = BCUC,
Отсюда 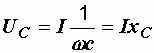 .
.
Последние три уравнения представляют разные формы записи закона Ома для конденсатора. Запишем их в символической форме. На основании (2.20) и (2.22):
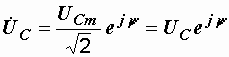 ,
,
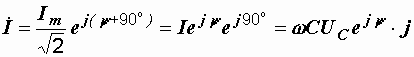 ,
,
или 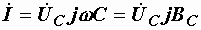 .
.
Отсюда 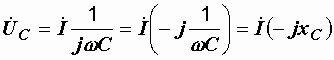 .
.
Векторная диаграмма, построенная по приведенным выше уравнениям, показана на рис. 2.22.
Угол наклона каждого вектора к положительному направлению вещественной оси определяется начальными фазами в выражениях (2.20) и (2.22). Так как при определении напряжения 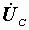 мы умножаем
мы умножаем 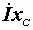 на –j, то вектор
на –j, то вектор 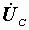 оказывается повернутым относительно вектора тока на угол 90° в отрицательном направлении, по часовой стрелке. Как отмечалось раньше, направление угла j на диаграмме показывается от вектора тока к вектору напряжения.
оказывается повернутым относительно вектора тока на угол 90° в отрицательном направлении, по часовой стрелке. Как отмечалось раньше, направление угла j на диаграмме показывается от вектора тока к вектору напряжения.
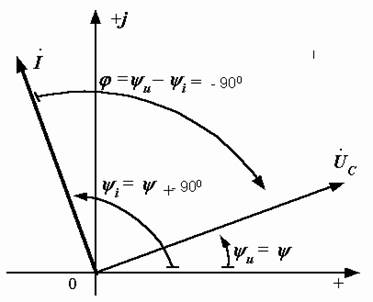
Рис. 2.22. Векторная диаграмма напряжения и тока в емкости
Пример 2.6. Напряжение на конденсаторе uC = 100sin (1000t –30° ). Написать выражение мгновенного значения тока через конденсатор. Каким станет ток, если частота питающего напряжения увеличится вдвое? Емкость конденсатора С = 50 мкФ.
Р е ш е н и е. Определяем емкостное сопротивление:
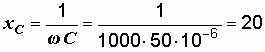 Ом.
Ом.
Амплитуда тока 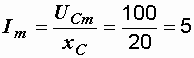 A.
A.
Так как 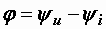 , а
, а 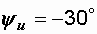 и
и 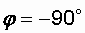 , то начальная фаза тока
, то начальная фаза тока
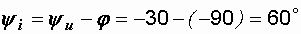 .
.
Таким образом, 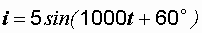 .
.
При возрастании частоты вдвое емкостное сопротивление уменьшается также вдвое: 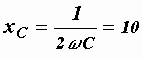 Ом.
Ом.
Амплитуда тока при этом увеличивается: 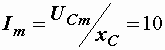 A.
A.
Так как угол сдвига фаз не меняется, то мгновенное значение тока будет равно
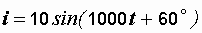 А.
А.
2.12. Последовательное соединение активного
сопротивления, индуктивности и емкости
В схеме, состоящей из последовательно соединенных активного сопротивления, индуктивности и емкости (рис. 2.23), заданы приложенное напряжение U, частота f и числовые значения параметров R, L и С. Требуется найти ток и напряжения на элементах
| При анализе электрических цепей синусоидального тока типична ситуация, когда метод решения незнакомой задачи неизвестен. Во многих случаях помогает следующий подход. По установленным ранее правилам строится векторная диаграмма, из анализа которой выводятся необходимые расчетные формулы. Так же поступим сейчас и мы. В последовательной цепи общим для всех элементов является протекающий по ним ток, поэтому именно с него начинаем построение векторной диаграммы. Проводим его изображение горизонтально (рис. 2.24). | 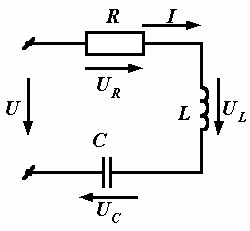 Рис. 2.23. Последовательная цепь переменного тока
Рис. 2.23. Последовательная цепь переменного тока
|
Вообще, направление первого вектора при построении диаграмм произвольно. Оно диктуется соображениями удобства. Дальше мы должны показать векторы напряжений на всех элементах и в соответствии со вторым законом Кирхгофа в векторной форме 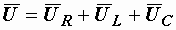 получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
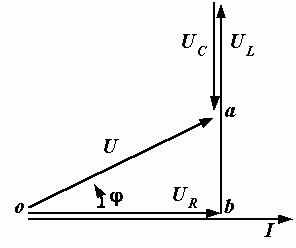
Рис. 2.24. Векторная диаграмма последовательной цепи
Нам известно, что напряжение на активном сопротивлении совпадает по фазе с током, поэтому вектор UR мы направляем по вектору I. К его концу пристраиваем вектор UL и направляем его вверх, так как напряжение на индуктивности опережает ток на 90° . Напряжение UС находится в противофазе с UL, т.е. отстает от тока на тот же угол 90° , поэтому вектор UС, пристроенный к концу вектора UL, направлен вниз. Векторная сумма UR, UL и UС дает вектор приложеного напряжения U.
Величины напряжений на отдельных элементах цепи нам известны:
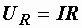 ,
, 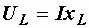 ,
, 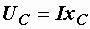 . (2.23)
. (2.23)
Из треугольника 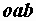 (рис. 2.24) по теореме Пифагора находим
(рис. 2.24) по теореме Пифагора находим
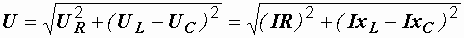 .
.
Вынося 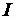 из под знака радикала, записываем последнее выражение в виде:
из под знака радикала, записываем последнее выражение в виде:
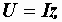 , (2.24)
, (2.24)
где z – полное сопротивление цепи, равное
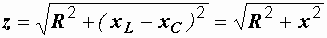 . (2.25)
. (2.25)
В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = хL – xC. Сами индуктивность и емкость называются реактивными элементами, и их сопротивления хL и xC тоже носят названия реактивных.
Выражение (2.24) называется законом Ома для всей цепи. Оно может быть записано и так:
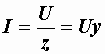 , (2.26)
, (2.26)
где 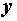 – полная проводимость цепи, представляющая величину, обратную полному сопротивлению:
– полная проводимость цепи, представляющая величину, обратную полному сопротивлению: 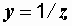 .
.
Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений 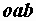 (рис. 2.24):
(рис. 2.24):
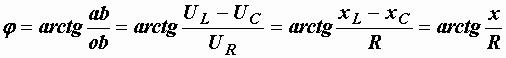 .
.
Векторная диаграмма на рис. 2.24 построена для случая, когда 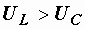 , что имеет место при
, что имеет место при 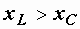 , когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.
, когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.
Возможны также режимы, когда 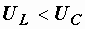 и
и 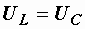 .
.
Пример 2.7. Параметры цепи на рис. 2.23, имеют следующие числовые значения: R = 60 Ом, xL = 40 Ом, xC = 120 Ом, U = 200 В.
Определить ток, напряжения на элементах и угол сдвига фаз между напряжением и током. Построить векторную диаграмму.
Р е ш е н и е. Определяем полное сопротивление цепи
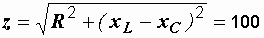 Ом.
Ом.
Действующее значение тока 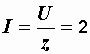 А.
А.
Напряжения на элементах:
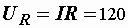 B,
B, 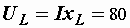 В,
В, 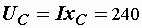 В.
В.
Угол сдвига фаз 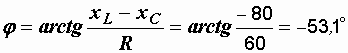
Векторная диаграмма показана на рис. 2.25. Так как 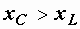 , цепь носит активно-емкостный характер, ток опережает напряжение, угол сдвига фаз j отрицателен и на диаграмме направлен от тока к напряжению в отрицательном направлении – по часовой стрелке.Типичным для цепей переменного тока является рассмотренный в задаче режим, когда напряжение на одном из реактивных элементов (в данном случае на емкости) превышает входное напряжение. При определенных соотношениях параметров цепи это превышение может быть довольно значительным – в десятки и сотни раз. , цепь носит активно-емкостный характер, ток опережает напряжение, угол сдвига фаз j отрицателен и на диаграмме направлен от тока к напряжению в отрицательном направлении – по часовой стрелке.Типичным для цепей переменного тока является рассмотренный в задаче режим, когда напряжение на одном из реактивных элементов (в данном случае на емкости) превышает входное напряжение. При определенных соотношениях параметров цепи это превышение может быть довольно значительным – в десятки и сотни раз.
| 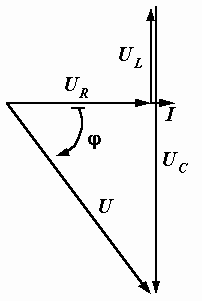 Рис. 2.25. Векторная диаграмма последовательной цепи
Рис. 2.25. Векторная диаграмма последовательной цепи
|
Обратим внимание также на то, что сумма падений напряжений на элементах в вольтах (120 + 80 + 240) не равна 200 – напряжению, приложенному к цепи. Еще раз повторяем, что для численных значений токов и напряжений законы Кирхгофа неприменимы. Они справедливы только для мгновенных значений, векторов и комплексных чисел. Показания приборов в цепях переменного тока складывать нельзя.
Пример 2.8. Определить величины сопротивления R и емкости С, если при частоте f = 50 Гц приборы в схеме на рис. 2.26, а имеют следующие показания: U = 125 В, UR = 100 В, I = 2,5 А.
Р е ш е н и е. По показаниям вольтметра и амперметра определяем величину активного сопротивления
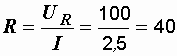 Ом.
Ом.
Для определения емкости конденсатора необходимо знать напряжение 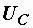 на его зажимах. Его можно найти из векторной диаграммы (рис. 2.26, б). При ее построении вектор
на его зажимах. Его можно найти из векторной диаграммы (рис. 2.26, б). При ее построении вектор 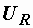 направляем по вектору тока – они совпадают по фазе, а вектор
направляем по вектору тока – они совпадают по фазе, а вектор 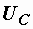 – под углом 90° к току в сторону отставания. Вектор входного напряжения
– под углом 90° к току в сторону отставания. Вектор входного напряжения 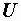 находим как сумму векторов
находим как сумму векторов 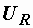 и
и 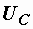 :
: 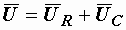 .
.
Из векторной диаграммы определяем напряжение на конденсаторе
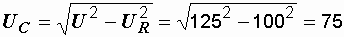 В.
В.
Теперь находим емкостное сопротивление:
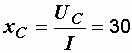 Ом.
Ом.
Из формулы 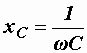 определяем емкость
определяем емкость
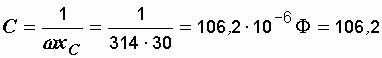 мкФ.
мкФ.
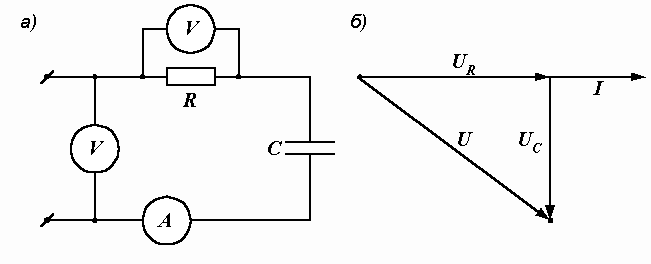
Рис. 2.26. Электрическая цепь и ее векторная диаграмма
Пример 2.9. К зажимам катушки с параметрами R = 30 Ом и L = 40 мГн приложено напряжение 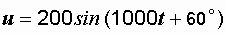 В. Записать выражение мгновенного значения тока. Каким оно станет, если частота питающего напряжения уменьшится вдвое?
В. Записать выражение мгновенного значения тока. Каким оно станет, если частота питающего напряжения уменьшится вдвое?
Р е ш е н и е. Вычисляем индуктивное и полное сопротивления:
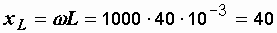 Ом,
Ом, 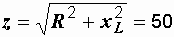 Ом.
Ом.
По закону Ома находим амплитуду тока
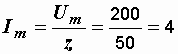 А.
А.
Определяем угол сдвига фаз
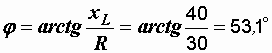 .
.
При отстающем токе (при активно-индуктивном характере цепи) этот угол положителен. Из (2.4) находим начальную фазу тока:
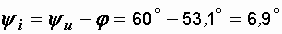 .
.
Итак 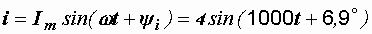 А.
А.
При уменьшении частоты, т.е. при 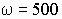 с-1:
с-1:
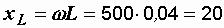 Ом,
Ом, 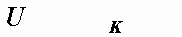 Ом,
Ом,
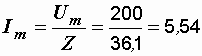 А,
А, 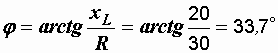 ,
,
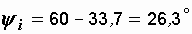 ,
, 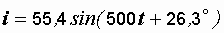 А.
А.
В схемах на рис. 2.27 предлагается определить показание вольтметра V на входе цепи, если во всех случаях показания вольтметров на отдельных элементах составляют V1 = 40 В, V2 = 30 В. Ответы на поставленный вопрос приводятся под каждой схемой.
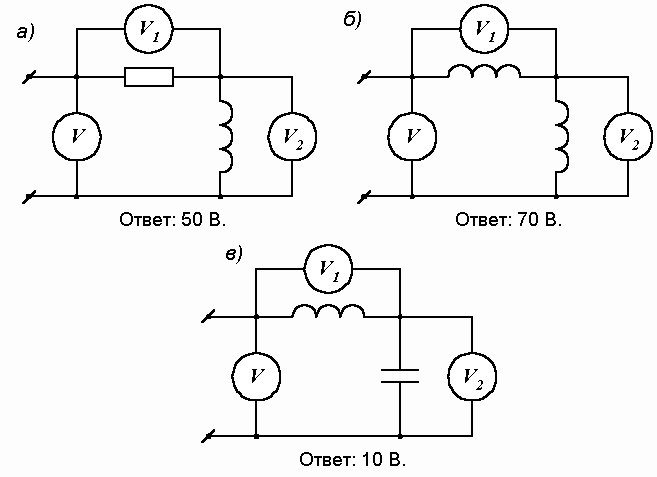
Рис. 2.27. Измерение напряжения в электрической цепи
Предлагаем учащемуся для каждого случая построить векторную диаграмму и проверить правильность приведенных ответов.
Вернемся к векторной диаграмме, представленной на рис. 2.24. Изобразим отдельно треугольник oab, являющийся ее частью (рис. 2.28, а). Этот треугольник называется треугольником напряжений.
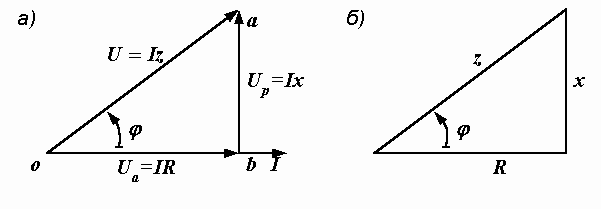
Рис. 2.28. Треугольники напряжений (а) и сопротивлений (б)
Проекция вектора напряжения на вектор тока называется активной составляющей напряжения. Она обозначается Uа и равна падению напряжения на активном сопротивлении 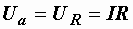 . Реактивная составляющая напряжения Ur – это проекция вектора напряжения на направление, перпендикулярное вектору тока. Она равна падению напряжения на суммарном реактивном сопротивлении цепи
. Реактивная составляющая напряжения Ur – это проекция вектора напряжения на направление, перпендикулярное вектору тока. Она равна падению напряжения на суммарном реактивном сопротивлении цепи 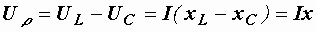 . Как видно из рис. 2.28, если все стороны треугольника напряжений разделить на ток, то получится подобный ему треугольник сопротивлений (рис. 2.28, б). Ему соответствуют следующие формулы:
. Как видно из рис. 2.28, если все стороны треугольника напряжений разделить на ток, то получится подобный ему треугольник сопротивлений (рис. 2.28, б). Ему соответствуют следующие формулы:
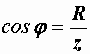 ,
, 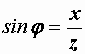 ,
, 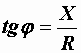 ,
, 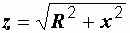 . (2.27)
. (2.27)
Решим задачу, поставленную в начале подразд. 2.12, символическим методом.
Запишем для цепи, изображенной на рис. 2.23, второй закон Кирхгофа в символической форме:
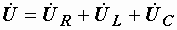 .
.
Подставляя в него напряжения на элементах, записанные ранее в комплексных числах 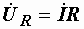 ,
, 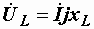 и
и 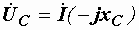 , получим:
, получим:
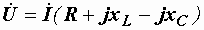 или
или 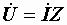 , (2.28)
, (2.28)
где 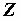 – комплексное сопротивление цепи, равное
– комплексное сопротивление цепи, равное
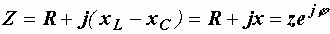 .
.
Выражение (2.28) представляет собой закон Ома в символической форме.
Пример 2.10. Определить показание амперметра в цепи, состоящей из последовательно соединенных сопротивлений – активного R = 60 Ом и индуктивного xL = 80 Ом, если напряжение на входе цепи U = 220 В.
Р е ш е н и е. Комплексное сопротивление цепи равно
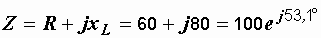 Ом.
Ом.
Для применения формулы (2.28) входное напряжениенеобходимо записать в символической форме, в виде комплексного числа 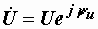 . Так как нам задано только его численное значение, начальную фазу (аргумент комплексного числа
. Так как нам задано только его численное значение, начальную фазу (аргумент комплексного числа 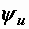 ) мы выбираем по своему усмотрению.
) мы выбираем по своему усмотрению.
Примем 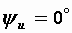 , тогда
, тогда 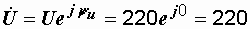 В.
В.
Комплекс действующего значения тока
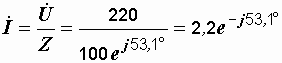 A.
A.
Показание амперметра равно модулю комплексного числа 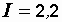 A.
A.
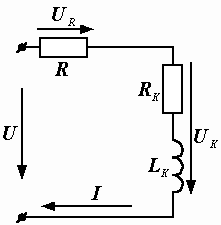
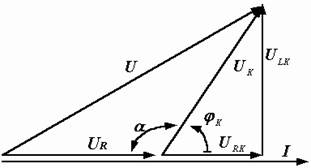
Пример 2.11. В цепи, состоящей из последовательно соединенных активного сопротивления R и катушки с параметрами RK = 34 Ом и хК = w LK = 48 Ом (рис. 2.29, а), известны UR = 100 B и UK = 120 В. Требуется найти напряжение на входе цепи U.
а)
| б)
|
Рис. 2.29. Электрическая цепь и её векторная диаграмма
Р е ш е н и е начинаем с построения векторной диаграммы (рис. 2.29, б). Вектор напряжения U равен векторной сумме напряжений 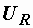 и
и 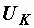 :
: 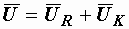 . Напряжение на катушке
. Напряжение на катушке 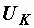 представляем как сумму напряжений на ее активном и реактивном сопротивлениях
представляем как сумму напряжений на ее активном и реактивном сопротивлениях 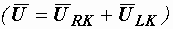 . Векторы
. Векторы 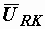 и
и 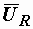 направляем по току, а
направляем по току, а 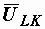 проводим перпендикулярно вверх.
проводим перпендикулярно вверх.
Величину входного напряжения, равную длине вектора U, можно найти одним из трех способов:
а) графически, построив векторную диаграмму в масштабе, для чего предварительно нужно рассчитать следующие величины:
– полное сопротивление катушки
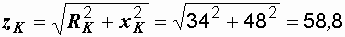 Ом;
Ом;
– ток в цепи
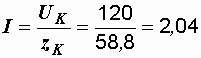 А;
А;
– составляющие напряжения на катушке
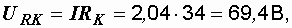
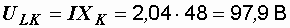 .
.
Измерив длину вектора U и умножив ее на масштаб, получим нужное нам значение;
б) решением треугольников, применяя известную из тригонометрии теорему косинусов: 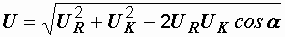 .
.
Угол a определяем из векторной диаграммы: 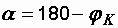 , где
, где
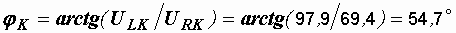 ,
, 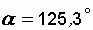 .
.
Вычисляем напряжение:
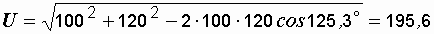 В;
В;
в) символическим методом, записав 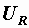 и и 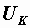 в комплексном виде и использовав уравнение второго закона Кирхгофа в символической форме в комплексном виде и использовав уравнение второго закона Кирхгофа в символической форме 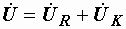 . Комплексные выражения . Комплексные выражения 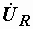 и и 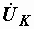 мы получим, изобразив векторы этих напряжений в комплексной плоскости, направив их из одного начала (рис. 2.30): мы получим, изобразив векторы этих напряжений в комплексной плоскости, направив их из одного начала (рис. 2.30):
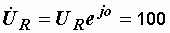 В; В; 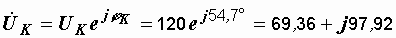 В. В.
| 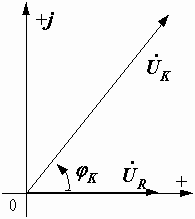 Рис. 2.30. Векторы в комплексной плоскости
Рис. 2.30. Векторы в комплексной плоскости
|
Находим 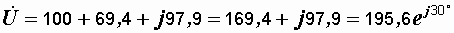 В.
В.
Величина напряжения 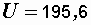 В.
В.
2.13. Параллельное соединение активного сопротивления,
индуктивности и емкости
Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а).
Требуется по известным G, ВL, ВC, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.
1. М е т о д в е к т о р н ы х д и а г р а м м.
Токи ветвей находятся сразу: 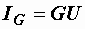 ,
, 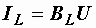 ,
, 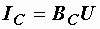 .
.
Для определения общего тока 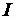 необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем
необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем
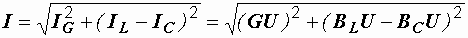
или 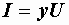 ,
,
где 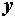 – полная проводимость цепи, равная
– полная проводимость цепи, равная
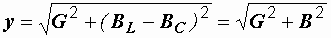 .
.
Разность индуктивной и емкостной проводимостей представляет собой общую реактивную проводимость цепи 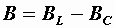 .
.
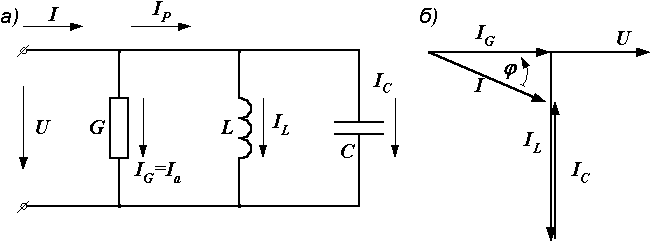
Рис. 2.31. Электрическая цепь и ее векторная диаграмма
Векторы токов на диаграмме образуют треугольник токов. Его горизонтальный катет, представляющий проекцию вектора тока на вектор напряжения, называется активной составляющей тока и равен току в активном элементе цепи: 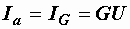 (рис. 2.32, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов
(рис. 2.32, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов 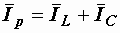 и определяется как разность длин векторов:
и определяется как разность длин векторов:
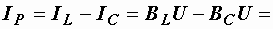
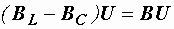 (см. рис. 2.31, б и 2.32, а).
(см. рис. 2.31, б и 2.32, а).
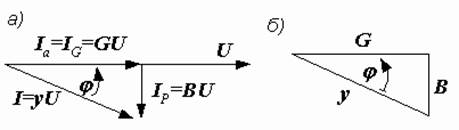
Рис. 2.32. Треугольники токов и проводимостей
Разделив все стороны треугольника токов на 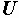 , получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:
, получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:
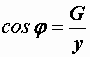 ,
, 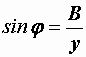 ,
, 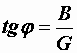 ,
, 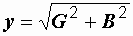 . (2.29)
. (2.29)
2. С и м в о л и ч е с к и й м е т о д.
Раньше были получены следующие формулы:
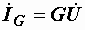 ,
, 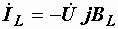 ,
, 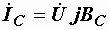 .
.
Подставляя их в уравнение первого закона Кирхгофа, получаем:
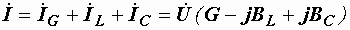 или
или 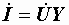 ,
,
где 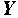 – комплексная проводимость цепи, равная
– комплексная проводимость цепи, равная
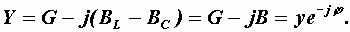
Пример 2.12. Для цепи, показанной на рис. 2.33, а, рассчитать токи, угол сдвига фаз между током и напряжением на входе цепи, построить векторную диаграмму. Числовые значения параметров цепи: 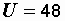 В,
В, 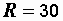 Ом,
Ом, 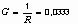 мкФ,
мкФ, 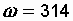 с-1.
с-1.
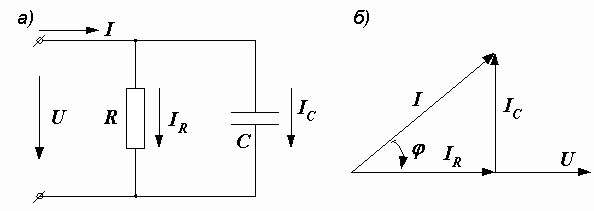
Рис. 2.33. Электрическая цепь и ее векторная диаграмма
Р е ш е н и е.
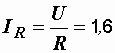 А,
А,  Ом,
Ом,
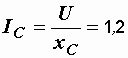 А,
А, 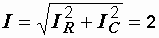 А.
А.
Векторная диаграмма приведена на рис. 2.33, б.
Угол сдвига фаз 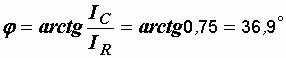 .
.
Величину общего тока можно найти иначе:
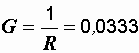 См,
См, 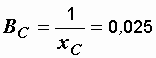 См,
См,
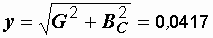 См,
См, 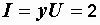 А.
А.
Пример 2.13. Начертить цепь, векторная диаграмма которой изображена на рис. 2.34, а.
Р е ш е н и е задачи показано на рис. 2.34, б.
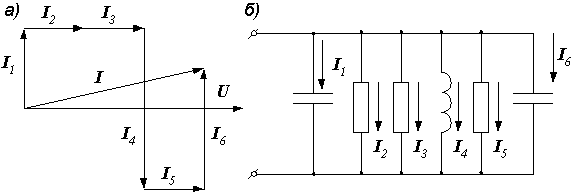
Рис. 2.34. Векторная диаграмма и соответствующая ей электрическая цепь
Пример 2.14. Чему равно показание амперметра А на входе цепи в схемах рис. 2.35, если амперметры А1 и А2 во всех случаях показывают соответственно 4 и 3 А?
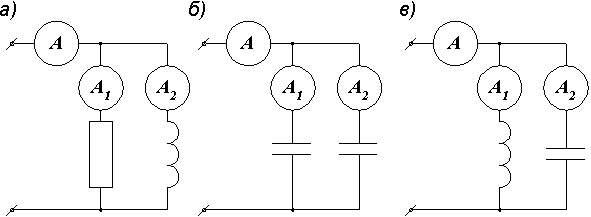
Рис. 2.35. Измерение тока в электрической цепи
Предлагаем для каждого случая самостоятельно построить векторную диаграмму и убедиться в правильности приведенных ответов: а) 5А, б) 7А, в) 1А.
2.14. Пассивный двухполюсник в цепи синусоидального тока.
Эквивалентные сопротивления и проводимости
На рис. 2.36 показан пассивный двухполюсник, состоящий из активных и реактивных элементов. Действующие значения напряжения 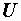 , тока
, тока 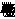 и угол сдвига фаз между ними
и угол сдвига фаз между ними 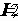 известны.
известны.
Построим по этим значениям векторную диаграмму и, спроектировав вектор напряжения на вектор тока и перпендикулярное к нему направление, получим треугольник напряжений, образованный сторонами 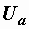 , , 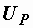 и и 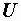 (рис. 2.37, а).
Как и раньше, (рис. 2.37, а).
Как и раньше, 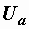 и и 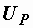 будем называть активной и реактивной составляющими напряжения. Изображенная в таком виде диаграмма соответствует схеме, показанной на рис. 2.37, б. Действительно, для нее будем называть активной и реактивной составляющими напряжения. Изображенная в таком виде диаграмма соответствует схеме, показанной на рис. 2.37, б. Действительно, для нее 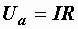 , , 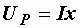 и и 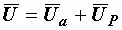 . .
| 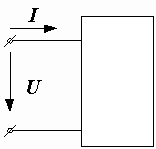 Рис. 2.36. Пассивный двухполюсник
Рис. 2.36. Пассивный двухполюсник
|
Схема называется последовательной схемой замещения или последовательной эквивалентной схемой пассивного двухполюсника, а ее параметры 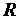 ,
, 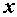 и
и 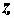 – эквивалентными сопротивлениями двухполюсника.
– эквивалентными сопротивлениями двухполюсника.
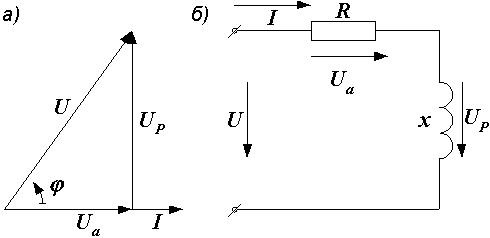
Рис. 2.37. Векторная диаграмма и соответствующая ей последовательная эквивалентная схема
Треугольник, образованный сторонами 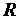 ,
, 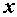 и
и 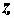 и подобный треугольнику напряжений, представляет собой треугольник сопротивлений (рис. 2.28, б), для которого справедливы формулы (2.27).
и подобный треугольнику напряжений, представляет собой треугольник сопротивлений (рис. 2.28, б), для которого справедливы формулы (2.27).
Теперь разложим в е к т о р т о к а на две составляющие – активную 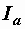 , направленную по вектору напряжения, и реактивную
, направленную по вектору напряжения, и реактивную 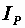 , перпендикулярную к нему (рис. 2.38, а). Такой векторной диаграмме соответствует параллельная схема замещения двухполюсника (рис. 2.38, б). Ее параметры
, перпендикулярную к нему (рис. 2.38, а). Такой векторной диаграмме соответствует параллельная схема замещения двухполюсника (рис. 2.38, б). Ее параметры 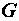 ,
, 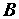 и
и 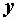 называются эквивалентными проводимостями. Токи в элементах
называются эквивалентными проводимостями. Токи в элементах 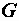 и
и 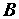 мы и представляем как активную и реактивную составляющие общего тока:
мы и представляем как активную и реактивную составляющие общего тока: 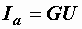 ,
, 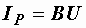 . Из треугольника токов (рис. 2.38, а) получается треугольник проводимостей
. Из треугольника токов (рис. 2.38, а) получается треугольник проводимостей
(рис. 2.32, б), стороны которого связаны между собой формулами (2.29).
а) б)
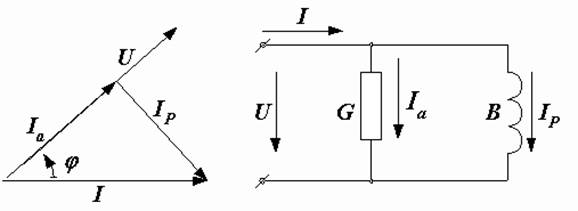
Рис. 2.38. Параллельная эквивалентная схема и ее векторная диаграмма
Получим условия эквивалентности приведенных схем.
Для последовательной цепи 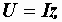 , для параллельной
, для параллельной 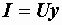 , а так как токи и напряжения в обеих схемах одинаковы, то
, а так как токи и напряжения в обеих схемах одинаковы, то
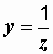 и
и 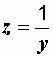 , (2.30)
, (2.30)
т.е. в любой электрической цепи полная проводимость есть величина, обратная полному сопротивлению.
Из сопоставления формул (2.27) и (2.29) можно записать:
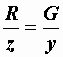 и
и 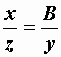 .
.
Рассматривая последние выражения совместно с (2.30), можно получить две группы формул:
| Формулы перехода от последовательной эквивалентной схемы к параллельной: | Формулы перехода от параллельной эквивалентной схемы к последовательной: |
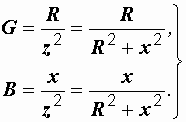 (2.31) (2.31)
| 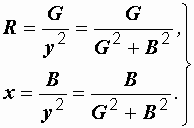 (2.32) (2.32)
|
Обращаем внимание на то, что каждая из проводимостей G и B зависит от обоих сопротивлений – активного и реактивного.
В свою очередь, каждое из сопротивлений определяется обеими проводимостями. Соотношения G = 1/R и B = 1/x справедливы только в частном случае, первое – при х = 0, второе – при R = 0.
Следует отметить, что активная и реактивная составляющие напряжения и тока физически не существуют, измерить их нельзя. Они относятся только к соответствующим эквивалентным схемам замещения и находятся расчетом. Более того, проектируя, например, вектор тока на различные напряжения, мы получим для него разные составляющие.
Пример 2.15. Найти общее сопротивление цепи, состоящей из параллельно соединенных активного R = 30Ом и индуктивного х = 40 Ом сопротивлений (рис. 2.39, а).
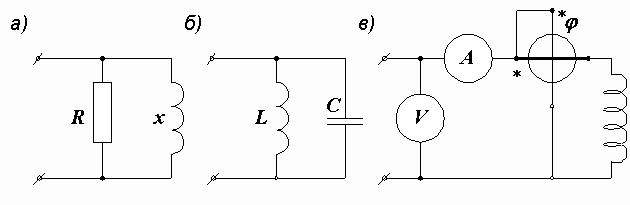
Рис. 2.39. Схемы к примерам 2.15–2.17
Р е ш е н и е. Так как в левой ветви реактивного сопротивления нет, то ее проводимость в соответствии с (2.31) равна G = 1/R. Аналогично, во второй ветви B = 1/x. Полная проводимость цепи 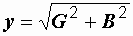 . В соответствии с (2.30) полное сопротивление цепи
. В соответствии с (2.30) полное сопротивление цепи
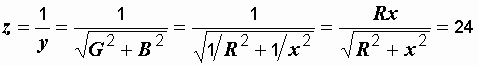 Ом.
Ом.
Пример 2.16. Рассчитать общее сопротивление цепи, состоящей из параллельно соединенных индуктивности L = 0,478 Гн и емкости С = 31,85 мкФ (рис. 2.39, б). Частота питающего напряжения f = 50 Гц.
Р е ш е н и е. Определяем сопротивления ветвей:
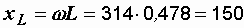 Ом,
Ом,
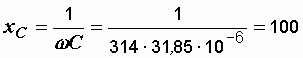 Ом.
Ом.
Так как в ветвях отсутствуют активные сопротивления, то их проводимости соответственно равны BL = 1/xL и BC = 1/xС. Полная эквивалентная проводимость цепи не содержит активной составляющей и равна
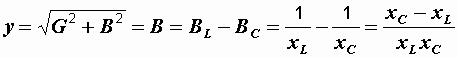 .
.
Полное эквивалентное сопротивление
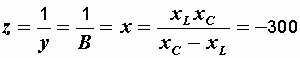 Ом.
Ом.
В рассматриваемой цепи активных элементов нет, она носит чисто реактивный характер. Он может быть индуктивным или емкостным. Знак минус в ответе свидетельствует о последнем, т.е. вся цепь может быть заменена конденсатором емкостью
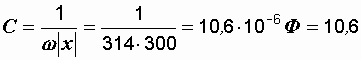 мкФ.
мкФ.
Пример 2.17. Амперметр А, вольтметр V и фазометр j , включенные в цепь катушки (рис. 2.39, в), дали следующие показания: U = 220 В, I = 4,4 А, cos j = 0,8. Частота питающего напряжения 50 Гц. Определить параметры последовательной и параллельной схем замещения катушки.
Р е ш е н и е. Находим параметры последовательной эквивалентной схемы:
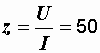 Ом,
Ом, 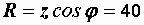 Ом,
Ом,
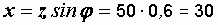 Ом.
Ом.
Рассчитываем элементы параллельной эквивалентной схемы:
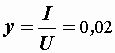 См,
См, 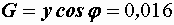 См,
См,
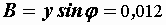 См.
См.
После определения эквивалентных сопротивлений эквивалентные проводимости можно было найти иначе, по формулам (2.31):
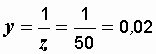 См,
См, 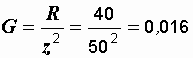 См,
См,
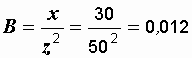 См.
См.
Пример 2.18. Рассчитать токи в схеме, приведенной на рис. 2.40.
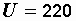 В, В,
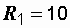 Ом, Ом,
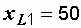 Ом, Ом,
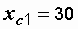 Ом, Ом,
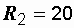 Ом, Ом,
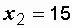 Ом, Ом,
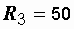 Ом, Ом,
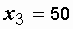 Ом. Ом.
| 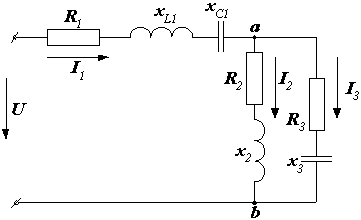 Рис. 2.40. Расчетная схема
Рис. 2.40. Расчетная схема
|
Р е ш е н и е. Определяем полные сопротивления второй и третьей ветвей:
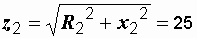 Ом,
Ом, 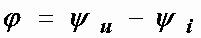 Ом.
Ом.
Преобразуем эти ветви в эквивалентные параллельные (рис. 2.41, а).
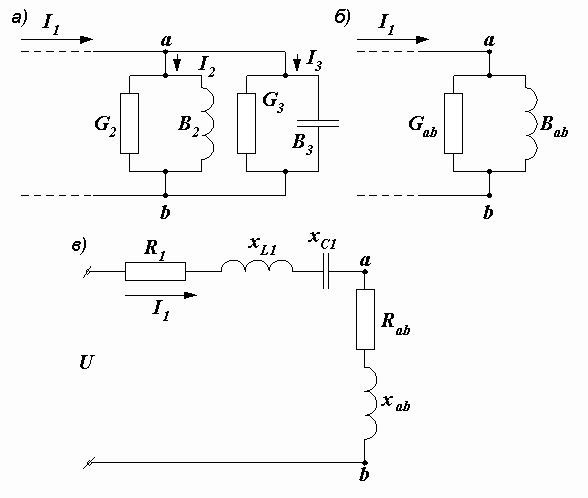
Рис. 2.41. Преобразования электрической цепи
Их проводимости:
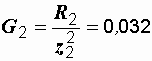 См,
См, 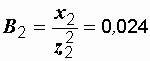 См,
См,
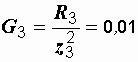 См,
См, 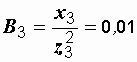 См.
См.
Суммируем активные и реактивные проводимости параллельных ветвей:
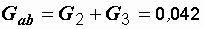 См,
См, 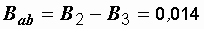 См (см. рис. 2.41, б).
См (см. рис. 2.41, б).
Определяем эквивалентные сопротивления участка 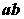 (рис. 2.41, в):
(рис. 2.41, в):
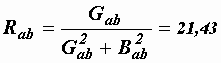 Ом,
Ом, 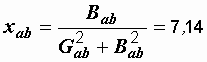 Ом,
Ом,
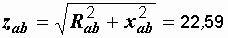 Ом,
Ом,
и полное сопротивление цепи:
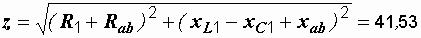 Ом.
Ом.
Ток на входе цепи I1 = U/z = 220/41,53 = 5,297 A.
Напряжение на участке 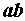 Uab= I1zab= 119,7 В.
Uab= I1zab= 119,7 В.
Токи второй и третьей ветвей:
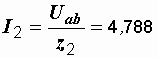 А,
А, 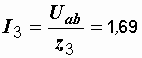 А.
А.
Еще раз напоминаем, что для численных значений токов и напряжений законы Кирхгофа неприменимы: 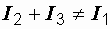 .
.
Дата добавления: 2020-10-14; просмотров: 616;











