Энергия и мощность в цепи синусоидального тока
Пусть на некотором участке цепи, напряжение на зажимах которого равно u, током i за время dt переносится электрический заряд dq = idt. Затрачиваемая источником энергия равна при этом dw = udq = uidt, а развиваемая мощность
p = dw/dt = ui. Эта величина называется мгновенной мощностью и определяет скорость и направление движения энергии на рассматриваемом участке. Если энергия поступает в цепь и накапливается в ней, функция w(t) возрастает, и мгновенная мощность положительна как производная возрастающей функции. Напряжение u и ток i в эти моменты времени имеют одинаковые знаки. Процесс накопления энергии в цепи наблюдается, например, при заряде конденсатора. В те моменты времени, когда u и i имеют разные знаки, мгновенная мощность отрицательна, функция w(t), определяющая энергию, поступающую в цепь, убывает, так как только убывающая функция имеет отрицательную производную. Убыль энергии в электрической цепи означает возврат ее источнику. Такая ситуация возникает при разряде конденсатора.
Энергия, поступающая в цепь, может не возвращаться к источнику, а необратимо преобразовываться в тепло или механическую работу. Количество этой энергии определяется законом Джоуля–Ленца и за время, равное периоду синусоидального тока, равно
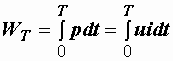 .
.
Эта величина, отнесенная ко времени Т, определяет среднее значение мгновенной мощности за период и называется активной мощностью
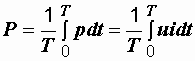 . (2.35)
. (2.35)
Физически активная мощность представляет собой энергию, выделяющуюся в виде тепла или механической работы в единицу времени.
Пусть ток и напряжение на входе произвольного пассивного двухполюсника описываются выражениями
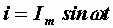 ,
, 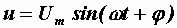 . (2.36)
. (2.36)
Подставляя их в (2.35) и интегрируя, получаем
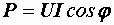 .
.
Используя соотношения между сторонами в треугольниках напряжений и токов, сопротивлений и проводимостей, можно написать цепочку формул для вычисления активной мощности:
 .
.
Рассмотрим теперь энергетические процессы, происходящие в отдельно взятых элементах.
В активном сопротивлении напряжение и ток совпадают по фазе (j = 0); в любой момент времени их знаки одинаковы, мгновенная мощность положительна, т.е. в него постоянно поступает энергия электрического тока, преобразуясь в тепловую или механическую. Активная мощность равна:
P = UI = I2R = U2G.
В реактивных элементах угол сдвига фаз по величине равен 90° . В индуктивности, при отстающем токе, он положителен, в емкости, при опережающем токе, – отрицателен. Подставляя j = ± 90° в выражение напряжения на входе цепи (2.36), получим u = Um sin (w t ± 90° ) =± Um cos w t. При таком напряжении мгновенная мощность колеблется с двойной частотой, изменяясь по синусоидальному закону
р = ± U I sin 2w t,
т.е. дважды за полпериода меняет знак. Подстановка этого выражения в (2.35) приводит к результату: P = 0. Равенство нулю активной мощности означает, что в реактивных элементах не происходит необратимого преобразования электромагнитной энергии в тепловую и механическую.
Можно показать, что в индуктивности в течение первой четверти периода, при возрастании тока от нуля до Im, в магнитном поле индуктивности накапливается энергия 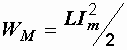 . В течение следующей четверти периода, когда ток уменьшается до нуля, эта энергия из магнитного поля возвращается во внешнюю цепь.
. В течение следующей четверти периода, когда ток уменьшается до нуля, эта энергия из магнитного поля возвращается во внешнюю цепь.
В емкости – аналогично: в течение одной четверти периода, когда напряжение на обкладках конденсатора возрастает от нуля до Um, конденсатор заряжается, в его электрическом поле накапливается энергия: 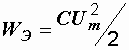 . В следующую четверть периода конденсатор разряжается, его напряжение уменьшается до нуля, и накопленная в электрическом поле энергия возвращается в цепь. Энергию, которой электрическое поле конденсатора и магнитное поле катушки обмениваются с цепью, будем называть энергией обмена.
. В следующую четверть периода конденсатор разряжается, его напряжение уменьшается до нуля, и накопленная в электрическом поле энергия возвращается в цепь. Энергию, которой электрическое поле конденсатора и магнитное поле катушки обмениваются с цепью, будем называть энергией обмена.
Для энергии магнитного поля WM и электрического поля WЭ можно записать следующие формулы:
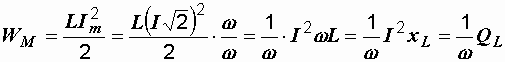 ,
,
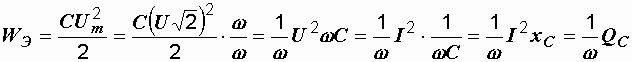 .
.
Величины 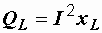 и
и 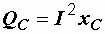 имеющие размерность мощности, называются соответственно реактивной мощностью индуктивности и реактивной мощностью емкости. К работе, совершаемой переменным током, они отношения не имеют, а являются величинами, пропорциональными энергии магнитного и электрического полей:
имеющие размерность мощности, называются соответственно реактивной мощностью индуктивности и реактивной мощностью емкости. К работе, совершаемой переменным током, они отношения не имеют, а являются величинами, пропорциональными энергии магнитного и электрического полей: 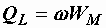 ,
, 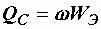 .
.
В цепи, содержащей одновременно и индуктивность и емкость, колебания энергии происходят таким образом, что в те моменты времени, когда магнитное поле индуктивности накапливает энергию, электрическое поле емкости энергию отдает, и наоборот. Т.е., когда энергия магнитного поля положительна, энергия электрического поля отрицательна. Суммарная энергия электрического и магнитного полей за четверть периода равна
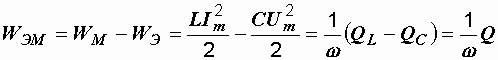 ,
,
где 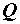 – реактивная мощность цепи, она пропорциональна суммарной энергии электрического и магнитного полей и может быть определена через реактивные сопротивления:
– реактивная мощность цепи, она пропорциональна суммарной энергии электрического и магнитного полей и может быть определена через реактивные сопротивления:
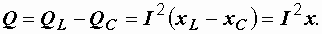
При резонансе, когда 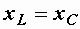 , равны реактивные мощности
, равны реактивные мощности 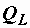 и
и 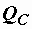 и энергии
и энергии 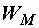 и
и 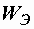 , накапливаемые в магнитном и электрическом полях. В этом случае обмен энергией между индуктивностью и емкостью происходит без участия источника.
, накапливаемые в магнитном и электрическом полях. В этом случае обмен энергией между индуктивностью и емкостью происходит без участия источника.
Для вычисления реактивной мощности можно написать цепочку формул, аналогичную (2.36):
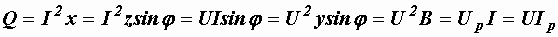 .
.
При анализе электрических цепей часто используется треугольник мощностей, который можно получить, умножив стороны треугольника сопротивлений на квадрат тока (рис. 2.47). Для него справедливы следующие соотношения:
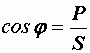 ,
, 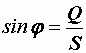 ,
, 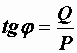 .
.
Буквой 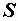 , стоящей рядом с гипотенузой треугольника, обозначается полная мощность. Ее можно вычислить по одной из следующих формул:
, стоящей рядом с гипотенузой треугольника, обозначается полная мощность. Ее можно вычислить по одной из следующих формул:
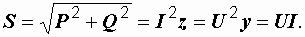
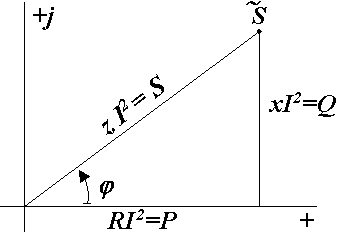
Рис. 2.47. Треугольник мощностей
Полная мощность определяется той электрической энергией, которая вырабатывается генератором и отдается в цепь. Она характеризует габариты электрических машин и аппаратов. Величина напряжения определяет уровень изоляции – ее толщину и расстояние между токоведущими частотами, а ток – поперечное сечение проводника, условия охлаждения машины.
При 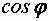 = 1 полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных напряжении и токе.
= 1 полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных напряжении и токе.
Единицы измерения мощности, имея одну и ту же размерность, называются по-разному. Единица активной мощности – ватт (Вт), реактивной – вольт-ампер реактивный (вар), полной – вольт-ампер (ВА).
Комплексная мощность определяется произведением комплекса напряжения и сопряженного комплекса тока:
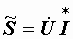 .
.
Пример 2.24. Рассчитать активную, реактивную и полную мощности цепи, если напряжение и ток на ее зажимах определяются выражениями: 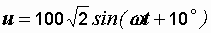 ,
, 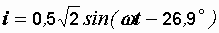 .
.
Р е ш е н и е. 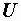 = 100 В,
= 100 В, 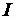 = 0,5 А,
= 0,5 А, 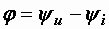 = 36,9° ,
= 36,9° , 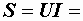 50 ВА,
50 ВА, 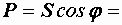 40 Вт,
40 Вт, 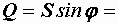 30 вар.
30 вар.
Или 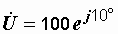 В,
В, 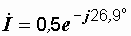 А,
А,
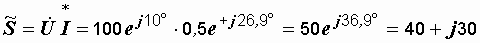 ВА.
ВА.
Дата добавления: 2020-10-14; просмотров: 549;











