Умови існування кривошипа в плоских чотириланкових механізмах

При проектуванні різних механізмів виникає потреба забезпечення неперервного обертання одних ланок відносно інших. Найчастіше такий рух є необхідним для вхідних ланок – кривошипів при використанні їх в як привода обертових двигунів. Таким чином важливою кінематичною характеристикою при синтезі механізму є прокручування ланок, тобто, наявність у нього одного чи двох кривошипів. Ця властивість залежить від співвідношення довжин ланок механізму і може бути наведена математично у вигляді деяких нерівностей.

Плоский шарнірний чотириланковик. Нехай задані довжини ланок l₁, l₂, l₃ та l₄ шарнірного чотириланковика АВСD (рис. 5.1, а). Потрібно з’ясувати, за яких умов ланка АВ буде кривошипом, тобто зможе провертатись на кут 360⁰ . Очевидно, що для цього вона повинна при обертанні послідовно пройти через крайнє ліве АВ₁ і крайнє праве АВ₂ положення. Іншими словами, необхідно, щоб існували трикутники В₁С₁D та В₂С₂ D. На основі властивості, що в будь-якому трикутнику довжина кожної сторони менша за суму довжин двох інших сторін, для ΔВ₁С₁D₁ та ΔВ₂С₂D ₂ можна записати такі нерівності

l₄+l₁ <l₂+l₃, (5.1)

l₄ - l₁<l₂+l₃ (5.2)

Нехай l₁ - довжина найкоротшої ланки, а l₄ - довжина найдовшої ланки. Тоді, незалежно від співвідношення між довжинами l₂ та l₃, нерівність (5.1) завжди забезпечить виконання нерівності (5.2). Якщо ж найдовшою є ланка ВС або СD (l₂>l₃>l₄ або l₃>l₂>l₄), то нерівність (5.1) тільки підсилюється.

Нерівність (5.1) дозволяє сформулювати умову існування кривошипа шарнірного чотириланковика, так зване правило Грасгофа: найкоротша ланка може бути кривошипом, якщо сума довжин найкоротшої та найдовшої ланок менша за суму довжин інших двох ланок.

Сформульована умова дозволяє поділити шарнірні чотириланковики на три групи механізмів: кривошипно - коромислові, якщо розміри ланок механізму задовольняють вказане правило та за стояк прийнято ланку, що розташована поруч з найкоротшою; двокривошипні, якщо розміри ланок задовольняють правило та за стояк прийнято найкоротшу ланку; двокоромислові, якщо розміри ланок не задовольняють правило, а також якщо задовольняють, але найкоротша його ланка є шатуном.

Кривошипно-повзунний механізм (рис. 5.1, б). Для цього механізму умова існування кривошипа визначається очевидною нерівністю

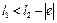, (5.3)

де е – зміщення механізму.

Якщо умова (5.3) не виконується, то ланка 1 є коромислом. У цьому разі механізм правильніше називати коромислово-повзунним.

На практиці, переважно застосовуються центральні кривошипно-повзунні механізми (е=0), для яких умова (5.3) приймає вид l₁<l₂.

Кулісний механізм. У кулісному механізмі ланка 1, незалежно від співвідношення між розмірами ланок завжди є кривошипом (рис.5.1, в). Щодо куліси 3, то вона буде кривошипом, якщо виконується умова

l₁>l₄ +e. (5.4)

В іншому випадку куліса не зможе здійснювати повний оберт, тобто буде коромислом. У першому випадку отримується так званий механізм з обертовою кулісою; в другому – механізм з коливною кулісою. В частковому випадку, якщо точку С віддалити у нескінченість, то коливна куліса перетвориться в кулісу, що рухається поступально. Зазначимо, що в техніці найрозповсюдженіші схеми кулісних механізмів, у яких зміщення е=0.

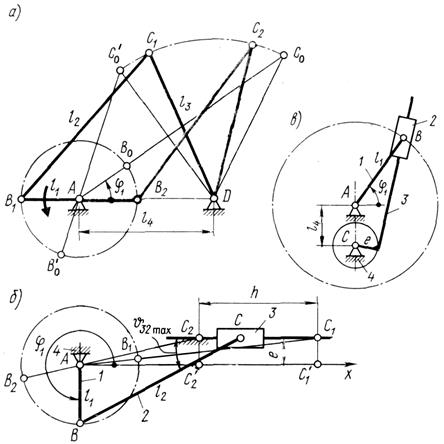
Рис. 5.1