Устойчивость динамической системы станка при резании.

С точки зрения устойчивости динамической системы станка при резании следует различать характер обработки: без повторного про­хода инструмента по ранее обработанной поверхности (обработка «по чистому») или с проходом режущей кромки по этой поверхности спустя некоторое время (обработка «по следу»).

Примером резания «по чистому» является нарезание винтовой ка­навки резцом, когда режущая кромка инструмента не попадает вторич­но в одно и то же место канавки. Обработка «по следу» более расп­ространена и встречается практически на всех станках. К ней отно­сятся фрезерование, сверление, зенкерование, большинство токарных, шлифовальных, расточных и других работ, в которых режущая кромка инструмента проходит по следу от предыдущего прохода (например, при обточке цилиндра на токарном станке след обработки вновь при­ходит к резцу через один оборот детали) или от впереди идущей ре­жущей кромки при работе многолезвийным инструментом (например, при фрезеровании зуб фрезы работает по следу от предыдущего зуба).

Рассмотрим методику определения устойчивости станка при резании «по чистому».

Динамическая система станка по связи с процессом резания ПР представляет собой замк­нутую систему с главными связями элементов ЭУС и ПР в виде упругой деформации станка у и силы резания Р. Условно разомкнув одну из главных связей замкнутой системы (рис. 10, а), получим разомкнутую систему (рис. 10, б), для ко­торой выражение передаточной функции W_paз(p) представляется произ­ведением передаточных функций УС и ПР (1.6):

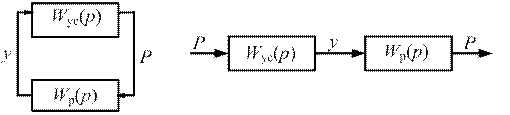
а) б)

Рис. 10. Замкнутая и условно разомкнутая динамическая система станка

Комплексную частотную характеристику разомкнутой системы, по которой с использованием критерия Найквиста можно судить об устой­чивости замкнутой системы, получаем из выражения передаточной функции

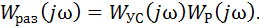
Выделив в этом выражении вещественную и мнимую составляющие, строим ее на комплексной плоскости в пределах рабочего диапазона частот

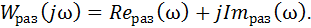
Эту же характеристику можно получить с использованием ха­рактеристик W_ус(jω) и W_р(jω) по правилам комплексных чисел (ампли­туды перемножаются, фазы складываются).

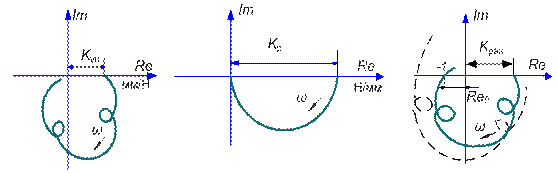
На рис. 11 показаны АФЧХ упругой системы (а), процесса ре­зания (б) и разомкнутой системы станка (в). Если W_paз(jω) не охва­тывает точку (-1; j0), как это показано сплошной линией, замкнутая система является устойчивой; если характеристика охватывает эту точку (пунктирная линия) – система неустойчива и обработка детали будет происходить с вибрациями. Чем больше отрезок Re₀, отсекаемый характеристикой на отрицательной части вещественной оси, тем ниже виброустойчивость системы.

а) б) в)

Рис. 11. Амлитудно-фазовые частотные характеристики (АФЧХ):

а) – упругой системы станка, б) – процесса резания, в) – разомкнутой динамической системы станка

Оценка виброустойчивости станка при обработке «по следу» осу­ществляется подобным способом, однако исходная модель динамической системы иная (рис. 12,а).

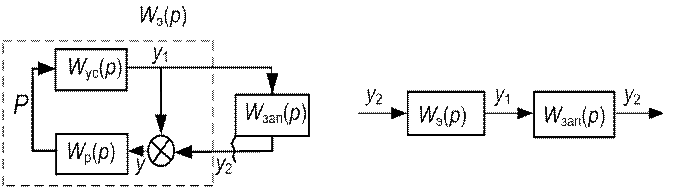
а) б)

Рис. 12. Динамическая система станка с учетом звена запаздывания:

а) – замкнутая; б) – условно разомкнутая.

При точении, растачивании или работе многолезвийным инструментом наличие следов создает дополнительную обратную связь с запаздыванием. Передаточная функция звена запаз­дывания W_зап(р) имеет вид

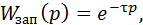
где τ – время запаздывания, с, равное времени одного оборота де­тали (при точении) или времени между проходом двух последующих ре­жущих кромок (при фрезеровании, зенкеровании и т.п.). Это время определяется частотой вращения шпинделя n, мин^-1, и числом режу­щих кромок инструмента z:

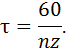
Заменяя замкнутый контур связи «ЭУС – ПР» эквивалентным эле­ментом с передаточной функцией W_э(р) и размыкая систему по связи с запаздыванием, получаем условно разомкнутую систему о двумя после­довательно соединенными элементами (рис. 12, б). Передаточная функция такой системы равна произведению передаточных функций этих элементов

где значение передаточной функции эквивалентного элемента определяется зависимостью (1.8) с учетом выражения (1.12)

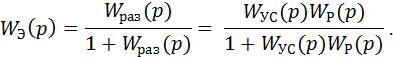
Комплексная частотная характеристика разомкнутой системы с учетом эвена запаздывания W_paз(jω) определяется из выражения пе­редаточной функции заменой оператора р на его значение jω

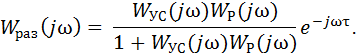
Построение характеристики разомкнутой системы с запаздыванием сводится к тому, что каждая точка характеристики эквивалентного элемента W_э( 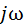) смещается вдоль окружности на угол φ, равный фазе звена запаздывания:

φ = – ωτ.

Оценка виброустойчивости станка с учетом влияния следов обра­ботки производится так. же, как и при обработке «по чистому», по положению характеристики W_paз ( 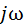) относительно точки (-1; j0). При этом возможны три варианта (рис 13):

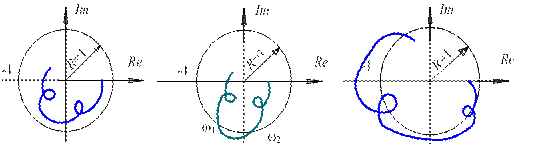
а) б) в)

Рис. 13. Варианты расположения АФЧХ разомкнутой системы

с учетом звена запаздывания

1. Система устойчива при любом значении τ, т.е. при любой частоте вращения шпинделя. В этом случае характеристика эквива­лентного элемента не выходит за пределы единичной окружности с центром в начале координат (рис. 13, а).

Для этого должно выпол­няться условие

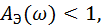
где A_э(ω) – значение амплитуды частотной характеристики эквива­лентного элемента в пределах рабочего диапазона частот ω.

2. Система устойчива в некоторых диапазонах изменения частоты вращения шпинделя. В этом случае характеристика эквивалентного элемента частично лежит за пределами единичной окружности (рис.13, б). Из условия

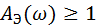
определяется диапазон частот ω₁…ω₂, в котором система может по­терять устойчивость.

Во многих случаях наблюдается несколько диапазонов частот вращения шпинделя с неустойчивой работой станка, т.е. характеристика экви­валентного элемента выходит за пределы единичной окружности неод­нократно. Методика определения этих диапазонов аналогична изложен­ной выше.

3. Система неустойчива при любом значении τ в пределах воз­можного сочетания nz. В этом случае при любой частоте вращения шпинделя характеристика эквивалентного элемента (рис. 13, в) ох­ватывает точку на комплексной плоскости с координатами (-1; j0). Достижение устойчивой работы станка возможно только изменением па­раметров упругой системы или процесса резания уменьшением их статических характеристик K_усили К_P.

Аналогично оценке виброустойчивости станка в процессе резания проводятся исследования динамики привода станка (рис.2а) по связи ЭУС с процессами в двигателе ПД, а также плавности перемещения рабочего органа станка на направляющих (рис. 2б) по связи ЭУС с процессом трения ПТ. Как видно из примеров на рис.2 расчетные схемы в этих случаях имеют своё специфическое изображение.

Список литературы

1. Кудинов В.А. Динамика станков. М.: Машиностроение, 1967. 359 с.

2. Дурко Е. М., Фецак С. И., Идрисова Ю. В. Динамика станков: учеб. пособие / Уфимск. гос. авиац. техн. ун-т. – Уфа: УГАТУ, 2014. – 132 с.

3. Линейные непрерывные САР: лабораторный практикум по дисциплине "Теория автоматического управления": ч.1/ Уфимск. гос. авиац. техн. ун-т; сост. Ю.В.Идрисова, С.И.Фецак.–Уфа:РИК УГАТУ, 2016.–68 с.

4. Чикуров Н. Г. Моделирование систем и процессов: Учеб. пособие. – М.: РИОР: ИНФРА-М, 2013. – 398 с.

5. Перевертайло Ю. В., Кудояров Р. Г., Фецак С. И. Влияние сил трения, действующих в приводе станка, на характер исполнительного движения // Вестник УГАТУ, 2009. Т.13, №1. С. 128 – 134.