ВРАЩАЮЩЕЙСЯ КОМПЛЕКСНОЙ ПЛОСКОСТИ

Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:

а) В цепи с активным сопротивлением ток и напряжение совпадают по фазе.

б) В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов

в) В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе на­пряжение на угол +90 градусов.

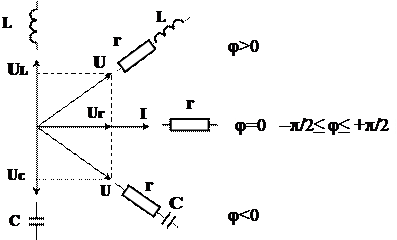
Рис.2.1.Мнемоническая схема, поясняющая возможные повороты

радиусов-векторов при различном включении r-L-C элементов.

При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включение элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи. Возможные сдвиги фаз векторов напряжения в электрических цепях, состоящих из различных комбинаций r-L-C элементов, приведены на мнемонической схеме (см. рис.2.1.).

Радиус-вектора на схеме и ниже выделяются жирным шрифтом или точками (черточками) над ними.

РЕЗОНАНС НАПРЯЖЕНИЙ В ЦЕПИ, СОСТОЯЩЕЙ ИЗ

ПОСЛЕДОВАТЕЛЬНО ВКЛЮЧЕНЫХ КАТУШКИ ИНДУКТИВНОСТИ

И КОНДЕНСАТОРА

Рассмотрим примеры такого анализа в предположении, что величины сопротивления, емкости и индуктивности не изменяются во времени и не зависят от приложенного напряжения и токов (см. рис.2.2).

Рис.2.2.Электрическая схема последовательно включенных r-L-C - элементов.

Процессы, происходящие в исследуемой цепи (в соответствии со вторым законом Кирхгофа) описываются (при постоянстве величин элементов во времени и независимости их от величины протекающего тока) линейным интегрально-дифференциальным уравнением:

u(t)=ri(t)+Ldi(t)/dt+1/C ∫i(t)dt, (2.31)

где u(t) – переменное напряжение, подаваемое от источника на колебательный контур,

i(t) – переменный ток, протекающий в цепи,

L – индуктивность,

r – активное сопротивление катушки индуктивности,

С – емкость конденсатора.

Сопротивление (r), индуктивность (L) и емкость (C) образуют колебательный контур, в котором возможен резонанс напряжений. Термин «резонанс напряжения» подразумевает, что при равенстве Х_l=Хc, переменные напряжения на элементах контура L и C увеличивается в Q раз по сравнению с напряжением подаваемым от источника на контур. Под величиной Q понимается добротность контура, равная Q=Хс/r.

Процессы, происходящие в исследуемой цепи (в соответствии со вторым законом Кирхгофа) описываются ( при постоянстве величин элементов во времени и независимости их от величины протекающего тока) линейным интегрально-дифференциальным уравнением.

При принятых предположениях уравнение (2.31) может быть представлено в следующем виде:

u(t)=i(t)*{r+j[X_l+Xc]}. (2.32)

Откуда следует выражение для комплексного сопротивления контура

Z=r+j{X_l–Xc}.

При резонансе напряжений, когда Х_l=Хс, Z=r, то есть сопротивление контура оказывается активным, а ток, протекающий через контур, достигает максимальной величины, равной i(t)макс=u(t)/r.

В данном случае построение векторной диаграммы надо начинать с общего для цепи вектора тока (Ỉ), затем строятся векторы напряжений. При последовательном соединении катушки индуктивности и емкости общее реактивное сопротивление цепи X равно алгебраической разности ин­дуктивного и емкостного сопротивлений Xl и Хc. Приложенное к такой цепи напряжение можно представить в виде векторной суммы вектора падения напряжения на активном сопротивлении (U r), совпадающего по фазе с вектором тока; вектора падения напряжения на индуктивности (U_l), опережающего ток по фазе на угол 90° и вектора падения напряжения на емкости (Uc), отстающего по фазе от вектора тока на угол 90°.При этом возможны следующие случаи:

а) Индуктивное сопротивление больше емкостного (Х_l >Х_С). В этом случае входное напряжение будет опережать ток по фазе на угол φ (см. рис. 2.3.).

б) Емкостное сопротивление больше индуктивного (Х_l<Х_с). При этом ток опережает напряжение на угол φ. Векторная диаграмма тока и напряжений показана на рис. 2.4.

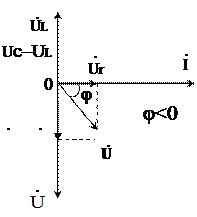Рис. 2.3 Рис. 2.4

в). Индуктивное сопротивление равно емкостному (Х_l=Xс). Соответственно полное реактивное сопротивление цепи (Х) равно нулю, а полное сопротивление цепи Z=r, т.е. достигает своего минимального значения. При этом ток будет по фазе совпадать с напряжением, т.е. угол φ=0.Векторная диаграмма токов и напряжений для этого случая приведена на рис. 2.5.

Явление резонанса напряжений происходит также в кварцевых резонаторах, которые широко используются в автогенераторах колебаний.