ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ЭДС, НАПРЯЖЕНИЙ И ТОКОВ ГАРМОНИЧЕСКИМИ ФУНКЦИЯМИ СО СЛУЧАЙНЫМИ, МЕДЛЕННО МЕНЯЮЩИМИСЯ АМПЛИТУДАМИ И ФАЗАМИ

Как уже отмечалось, параметры электромагнитного поля – случайные величины и при их описании необходимо использовать математический аппарат теории случайных процессов. Особенно удобно использовать математический аппарат случайных процессов в тех случаях, когда электродвижущие силы и напряжения носят колебательный характер и могут быть представлены случайными функциями времени. Такое представление хорошо согласуется с экспериментальными данными и может использоваться для описания электромагнитных полей, создаваемых как оптическими квантовыми генераторами (ОКГ), так и генераторами электромагнитных излучений всех типов, работающих на более низких частотах вплоть до долей Герца.

В системах электроснабжения предприятий случайный характер изменения напряжений и тока определяется прежде всего непрерывными изменениями величины тока нагрузки. Кроме того величина напряжения, вырабатываемого каждым из генераторов, изменяется случайным образом вследствие изменения во времени магнитного потока, параметров цепей возбуждения и нестабильности скорости вращения ротора генератора. Случайные флуктуации мощности возникают в линиях передачи электроэнергии также из-за нелинейности характеристик нагрузок электрической сети.

Из-за случайного характера колебаний напряжения в электрической сети ширина энергетического спектра на уровне -3 дБ, оказывается обычно равной 1..2 Гц; а на уровне - 80 дБ, равным -40 Гц . Центральная частота спектра часто не совпадает с номинальной частотой, равной 50 Гц. Как показывают измерения, в некоторых энергетических системах центральная частота спектра отличается на 1-2 Гц от номинальной.

АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ Э.Д.С.,

НАПРЯЖЕНИЙ И ТОКОВ

Таким образом, при достаточно общих предположениях, хорошо выполняющихся на практике, электродвижущую силу (э.д.с.), переменное напряжение и ток, можно представить в виде произведения случайной амплитуды Um(t) и гармонической функции случайной фазы Ψ (t).

Как известно, такое представление электрических величин требует наложения определенных ограничений на сомножители, которые в общем случае нельзя выбирать произвольно. Для устранения неоднозначности наиболее целесообразно использовать представление переменного напряжения в электрической цепи в комплексном аналитическом виде:

; (2.4)

где 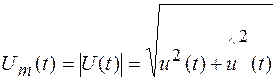; (2.5)

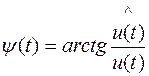, (2.6)

u(t) ‑ реальное напряжение в электрической цепи;

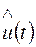-дополняющая компонента, связанная с u(t) преобразованием Гильберта:

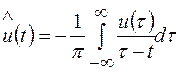(2.7)

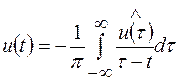(2.8)

При этом выражение для реального напряжения может быть представлено в виде:

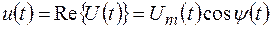(2.9)

Такое представление переменного (в общем случае случайного) напряжения u(t) имеет следующие преимущества:

а) амплитуда и фаза напряжения связаны между собой единственным образом, что исключает неоднозначность;

б) комплексный спектр напряжения U(w)отличен от нуля только при положительных w, причем спектры напряжений u(t) и 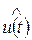совпадают по форме и отличаются только масштабным множителем, т.е. спектр комплексного напряжения в этом случае имеет ту же структуру, что и спектр исходного реального напряжения u(t);

в) представление переменного напряжения в комплексном виде (2.9) может быть применимо как к быстро, так и к медленно изменяющимся напряжениям в электрических и электронных цепях,

В тех случаях, когда зависимость напряжения от времени u(t) характеризуется быстрым изменением со средней круговой частотой wср=2pfср, можно считать, что за время, равное по крайней мере нескольким периодам, амплитуда и фаза остаются практически неизменными.

Выражение для комплексного аналитического представления переменного флуктуирующего напряжения может быть записано в виде:

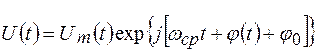(2.10)

или 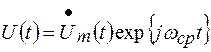(2.11)

где 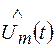- комплексная огибающая узкополосного случайного процесса:

(2.12)

- средняя круговая частота, определяемая выражением:

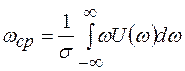(2.13)

где 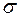-дисперсия флуктуаций напряжения, квадрат которой определяется из выражения:

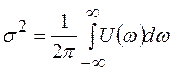(2.14)

– энергетический спектр напряжения 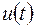, определяющийся выра­жением:

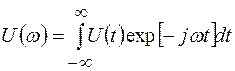(2.15)