ИЗУЧЕНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ И КОМБИНАЦИОННЫХ УСТРОЙСТВ
В ЭВМ, цифровых измерительных приборах и других цифровых устройствах широко применяются логические элементы (ЛЭ). Каждый ЛЭ выполняет вполне определенную логическую операцию над цифровой информацией. ЛЭ создают на базе электронных устройств, работающих в ключевом режиме. Ключевой режим характеризуется двумя состояниями ключа: включено — отключено. Поэтому любую информацию необходимо преобразовать в цифровой двоичный код, при котором цифра каждого разряда принимает только два значения: 0 (логический нуль) и 1 (логическая единица). Это соответствует двум состояниям ключа.
Для описания логических операций используется математический аппарат, получивший название алгебры логики, или булевой алгебры в честь его создателя — ирландского ученого Джорджа Буля. Алгебра логики изучает взаимосвязь между простыми высказываниями, образующими сложные высказывания. Исходя из булевой алгебры простое высказывание может иметь только два значения — истинное (true) или ложное (false). Одно из этих значений принимается за единицу, второе — за нуль. Уровень выходного напряжения ЛЭ зависит от уровня входного (или нескольких входных) напряжения. Эта связь отображается формулой и таблицей состояний, или таблицей истинности.
Логические операции преобразуют по определенным правилам входную информацию, обозначаемую символами Х1, Х2, Х3, ..., Хn, в выходную, которую обозначим буквой F. Условные обозначения основных логических элементов показаны на рисунке 10.1, таблица истинности приведена в таблице 10.1 для двух значений входных сигналов — Х1 и Х2.
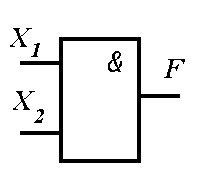
| 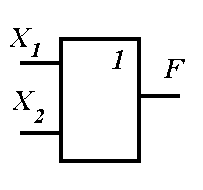
| 
|
| а) | б) | в) |
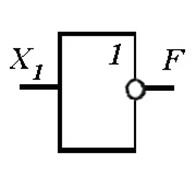
Рисунок 10.1 — Графические обозначения основных логических элементов (операций):
а — элемент «И», б — элемент «ИЛИ», в — элемент «НЕ»
Рассмотрим основные логические операции.
1. Логическое умножение (конъюнкция), или операция «И», обозначается в формулах булевой алгебры знаками «*» или «^». Символически операция записывается выражениями:
F = Х1 * Х2 * Х3 * … * Хn или F = Х1 ^ Х2 ^ Х3 ^… ^ Хn.
Логика срабатывания этой операции состоит в том, что на выходе ЛЭ будет сигнал «1» только в том случае, если на и X1,и Х2,и Х3, и т.д.входы поступят, т.е. если на входах будут все сигналы, предусмотренные в данной операции (все true), то и на выходе будет сигнал (truе). При этом ложное высказывание будет истинным, если истинны все простые высказывания.
Графическое обозначение операции — рисунок 10.1, а.
2. Логическое сложение (дизъюнкция), она же операция «ИЛИ», обозначается знаками «+», « 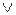 ». Символически операция записывается следующими выражениями:
». Символически операция записывается следующими выражениями:
F = Х1 + Х2 + Х3 + … + Хn; F = Х1 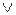 Х2
Х2 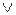 Х3
Х3 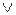 …
… 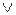 Хn.
Хn.
Логика срабатывания этой операции состоит в том, что на выходе ЛЭ «ИЛИ» будет сигнал «1» в том случае, если на его входы или Х1, или Х2, или Х3 и т.д.поступит хотя бы один сигнал «1» из всех предусмотренных. Другими словами, сложное высказывание будет истинным (truе), если истинно хотя бы одно из простых высказываний, и ложным (false), если ложны (false) все простые высказывания. Графическое обозначение операции — рисунок 10.1, б.
3. Логическое отрицание (инверсия), или «НЕ», обозначается чертой над входной (входными) переменной. Символически записывается:
 .
.
На схемах условное обозначение этой логической операции — кружочек на выходе прямоугольника (рисунок 10.1, в). Смысл этой операции состоит в том, что на выходе этого ЛЭ сигнал будет лишь в том случае, если на входе сигнала нет. Если на входе есть сигнал, то на выходе он отсутствует. Это простое отрицание, которое используется сравнительно редко.
Гораздо чаще используется операция «НЕ» в сочетании с операциями «И» или «ИЛИ». Рассмотрим такие составные операции.
4. Отрицание логического умножения, или операция «И-НЕ». Графическое обозначение операции — рисунок 10.2, а. Символически операция записывается выражениями:
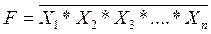 или
или 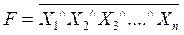 .
.
Логика срабатывания операции «И-НЕ» заключается в том, что сигнал на выходе этого ЛЭ будет в том случае, если отсутствует сигнал хотя бы на одном входе. Эта операция известна также под названием «штрих Шеффера», образует сложное высказывание из простых по следующему правилу: сложное высказывание истинно, если ложно хотя бы одно из простых высказываний, и ложно, если все простые высказывания истинны (см. таблицу 10.1).
На входы ЛЭ при любой логической операции подается вполне определенное количество входных сигналов, поэтому и в символике записи это находит отражение. Например, если на входы подаются два сигнала, то получим «2И-НЕ», если три сигнала, то «3И-НЕ», или символьно:
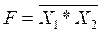 ,
,  соответственно и так далее.
соответственно и так далее.
5. Отрицание логического сложения, или операция «ИЛИ-НЕ». Графическое обозначение операции — рисунок 10.2, б. Символически операция записывается выражениями:
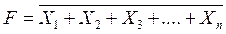 или
или 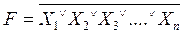
Смысл этой операции состоит в том, что на выходе этого устройства сигнал будет лишь в том случае, если нет сигналов на его входах. Если появится сигнал хотя бы на одном входе ЛЭ, реализующего операцию «ИЛИ-НЕ», то на выходе сигнала не будет. Операция «ИЛИ-НЕ» называется также «стрелкой Пирса», образует сложное высказывание из простых в соответствии со следующим правилом: сложное высказывание истинно лишь в том случае, когда ложны все образующие его простые высказывания, и ложно, если истинно хотя бы одно из простых высказываний (см. таблицу 10.1).
На входы ЛЭ при любой логической операции подается вполне определенное количество входных сигналов, поэтому и в символике записи это находит отражение. Например, если на входы подаются два сигнала, то получим: «2ИЛИ-НЕ», если три сигнала, то «3ИЛИ-НЕ», или символьно
 ,
, 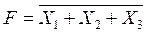 соответственно и так далее.
соответственно и так далее.
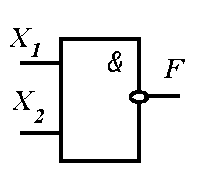
| 
|
| а) | б) |
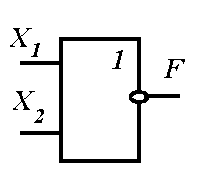
Рисунок 10.2 — Графические обозначения составных логических элементов (операций):
а — элемент «И-НЕ»; б — элемент «ИЛИ-НЕ»
Таблица 10.1
| X1 | X2 | F | |||
| «И» | «ИЛИ» | «2И-НЕ» | «2ИЛИ-НЕ» | ||
В зависимости от вида используемых сигналов ЛЭ подразделяют на потенциальные, в которых «0» (false) или «1» (true) задаются двумя различными уровнями постоянного напряжения. Низкий уровень напряжения соответствует «0», высокий — «1». Также ЛЭ бывают импульсными, в которых «0» означает отсутствие импульса, а «1» соответствует наличию импульса. Наибольшее распространение получили потенциальные ЛЭ.
ЛЭ выполняются чаще всего на основе интегральных микросхем (ИМС) определенной серии, например К155.
В данной лабораторной работе исследуются логические элементы
«2И-НЕ»(К155ЛАЗ) и «2ИЛИ-НЕ» (К155ЛЕI), условные обозначения которых показаны на рисунке 10.2, а и б соответственно.
На основе этих базовых ЛЭ могут быть созданы комбинационные логические устройства, выполняющие операции любой сложности. В комбинационных устройствах сигнал на выходе F определяется комбинацией входных сигналов Х1, Х2, Х3, … .
Пусть требуется создать комбинационную схему с тремя входами Х1, Х2, Х3 и одним выходом F. Высокий уровень напряжения на выходе должен появляться только при высоких уровнях на входах Х1 и Х2, т.е. F = 1 при Х1 = Х2 = 1 и Х3 = 0.
Любую комбинационную схему можно составить путем подбора элементов. В данном случае, если использовать ЛЭ с двумя входами, а именно «2И-НЕ» и «2ИЛИ-НЕ», то она будет содержать не менее четырех входов. Три входа необходимы для входных величин Х1, Х2, Х3 и один вход можно использовать для связи между ЛЭ.
Так как схема должна реагировать на появление одинаковых высоких уровней (или импульсов) Х1 и Х2, то эти входы следует объединить ЛЭ «2И-НЕ». На его выходе получим низкий уровень при наличии Х1 = Х2 = 1.
Следовательно, второй ЛЭ должен давать на выходе высокий потенциал F = 1 только при поступлении на его входы двух низких уровней, т.е. при отсутствии сигналов на его двух входах. Поэтому таким вторым элементом схемы является ЛЭ «2ИЛИ-НЕ» (рисунок 10.3).
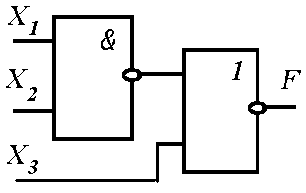
Рисунок 10.3 — Простейшее комбинационное устройство на основе логических элементов
При большом числе входов такой метод подбора трудоёмок. Более рационально составление уравнения логической функции и последующая ее декомпозиция и оптимизация по правилам булевой алгебры, или алгебры логики. Для данного случая представление операции выразится формулой:
 .
.
Чтобы разобраться, какие ЛЭ здесь необходимо взять, надо его
преобразовать, используя тождество  . Оно означает, что двойное «НЕ» может означать «ДА». Кроме того, здесь надо применить формулы Моргана:
. Оно означает, что двойное «НЕ» может означать «ДА». Кроме того, здесь надо применить формулы Моргана:
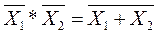 и
и 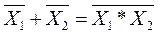
Смысл первой формулы заключается в том, что если отсутствуют первый Х1 и второй Х2 сигналы (операция логического умножения отсутствующих сигналов), то операция переходит в логическое «2ИЛИ-НЕ», т.е. на выходе отсутствует сигнал, так как нет Х1 или Х2 (по сути дела, их нет обоих).
Смысл второй формулы состоит в том, что если нет сигнала Х1 или Х2 (операция логического сложения отсутствующих сигналов), то операция переходит в «2И-НЕ», т.е. на выходе нет сигнала, так как нет Х1 и нет Х2.
Исходя из этого, формулу рассматриваемой операции можно преобразовать следующим образом:
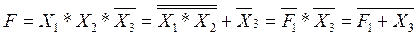 ,
,
где 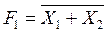 — введенное обозначение.
— введенное обозначение.
Полученное выражение показывает, что, во-первых, нужен ЛЭ
«2ИЛИ-НЕ», чтобы выполнить операцию 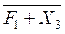 , во-вторых, нужен ЛЭ
, во-вторых, нужен ЛЭ
«2И-НЕ», осуществляющий операцию в соответствии с 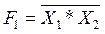 .
.
Многие комбинационные устройства, встречающиеся в цифровой вычислительной технике (шифраторы, дешифраторы, сумматоры), представляют собой готовые ИМС. В данной работе используется четырехразрядный сумматор, выполненный на микросхеме К155ИМЗ, структурная схема которого показана на рисунке 10.4. Состоит он из четырех одноразрядных сумматоров SМ. Каждый одноразрядный сумматор имеет три входа: два входа А и В для ввода двух суммируемых чисел одного разряда и вход Р-перенос, на который поступает сигнал с выхода предыдущего разряда как результат сложения в нем чисел. На выходе S появляется сигнал, соответствующей сумме двух чисел двоичного кода, а на выходе Р— сигнал переноса, если в результате сложения получается двухзначное число. Например, необходимо сложить два двоичных четырехразрядных числа — А = 0101 (десятичное число 5) и В = 1001 (9). На входы сумматора поступят А0 = 1 и В0 = 1, в результате получится в двоичном коде 1 + 1 = 10 (в десятичном коде 2). Поэтому на выходе S0 =0, а Р = 1. На входы второго сумматора поступят А1 = 0, В1 = 0, Р = 1. На выходе получится единица в этом разряде S1 = 1 и Р = 0, т.е. в следующий разряд нуль переносится. На третьем сумматоре А2 = 1, В2 = 0 и Р = 0. В результате получится S2 = 1, Р = 0 (см. таблицу 10.2).

Рисунок 10.3 — Схема четырехбитного сумматора
Таблица 10.2
| Числа | Двоичный код | Десятичный код |
| A | 0 1 0 1 | |
| B | 1 0 0 1 | |
| A+B | 1 1 1 0 |
Сумматор с большим числом разрядов объединяет несколько простых.
ЛИТЕРАТУРА
1. Касаткин, А.С. Электротехника / А.С. Касаткин, М.В. Немцов. — Москва: Энергоатомиздат, 1983.— 427 с.
2. Посудевский, А.А. Электропитание радиоэлектронных средств / А.А. Посудевский. — Москва: Воениздат, 1980. — 248 с.
3. Кiтуновiч, Ф.Г. Электратэхнiка / Ф.Г. Кiтуновiч. — Мiнск: Вышэйшая школа, 1998. — 429 с.
4. Автомобиль. Основы конструкции / Н.Н. Вишняков [и др.]. — Москва: Машиностроение, 1986.
5. Электротехника / Б.А. Волынский, В.Н. Зейн, В.Е. Шатерников. — Москва: Энергоатомиздат, 1987.
6. Асинхронные машины / под ред. И.П. Копылова. — Москва: Высшая школа, 1977. 328 с.
7. Осин, И.Л. Электрические машины. Синхронные машины / И.Л. Осин, Ю.Г. Шакарян; под ред. И.П. Копылова. — Москва: Высшая школа, 1990. 304 с.
8. Хвостов, В.С. Электрические машины. Машины постоянного тока / В.С. Хвостов; под ред. И.П. Копылова. — Москва: Высшая школа, 1989. — 335 с.
9. Морозов, А.Г. Электротехника, электроника и импульсная техника / А.Г. Морозов. — Москва: Высшая школа, 1987.
10. Галкин, В.И. Промышленная электроника / В.И. Галкин. — Минск: Вышэйшая школа, 1989.
11. Лабораторные работы (практикум) по курсу «Электротехника и электроника» для студентов неэлектрических специальностей: Ч. 3. Электроника / Розум Т.Т. [и др.]. — Минск: БГПА, 1988.
Дата добавления: 2020-10-14; просмотров: 521;











