В РАЗЛИЧНЫХ РЕЖИМАХ РАБОТЫ
Процесс измерения любой физической величины любым измерительным прибором требует некоторых временных затрат. Минимально допустимое время измерения определяется постоянной прибора, т. е. его инерционными свойствами.
С другой стороны, измеряемая величина может изменяться во времени с различной скоростью. Соотношение между скоростью изменения измеряемой величины и постоянной измерительного прибора определяет режим его работы. Различают два режима работы: статический и динамический.
Режим работы измерительного прибора называется статическим, если измеряемую величину (параметр) на интервале измерения можно считать постоянной. Когда измеряемый параметр изменяется в процессе измерения, измерительный прибор переходит в динамический режим. В последнем случае для определения результата измерения необходимо учитывать динамические свойства прибора. Погрешности измерений увеличиваются.
Таким оборазом, свойства средств измерений, прежде всего точность, во многом зависят от режимов работы. В лекции рассматриваются погрешности средств в различных режимах.
1. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ
ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
Для упрощения анализа свойств средств измерений, вводятся понятия: звено и структурная схема. Определим эти понятия.
В средствах измерений сигнал претерпевает сложное функциональное преобразование, которое всегда можно разложить на ряд элементарных. Можно считать, что каждое элементарное преобразование происходит в отдельном функциональном узле. Функциональный узел, осуществляющий элементарное преобразование измеряемого сигнала, получил название «звено». Соединение звеньев в цепь преобразований называется структурной схемой.
В зависимости от соединения звеньев различают два вида структурных схем: прямого преобразования (действия) и уравновешивающего (компенсационного).
1.1. Средства измерений прямого преобразования.
Структурная схема этих средств приведена на рисунке 12.1.

В приведенной схеме индексами 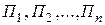 обозначены звенья; индексами
обозначены звенья; индексами 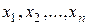 - информативные параметры сигналов измерительной информации. Для краткости будем называть их сигналами.
- информативные параметры сигналов измерительной информации. Для краткости будем называть их сигналами.
Схему прямого преобразования имеют электромеханические приборы, например, амперметр. Для амперметра входным сигналом х является измеряемый ток I. Посредством шунта (звено П1) ток I преобразуется в малый ток I1, соответствующий на схеме сигналу х1. Следующее звено схемы – П2 представляет узлы измерительного механизма, преобразующие электрическую величину I1 в значение вращающего момента М, т. е. в сигнал х2. Звено П3 преобразует вращающий момент в угол поворота указателя α, что соответствует сигналу х3.
Чувствительность прибора по рис. 12.1 определим выражением
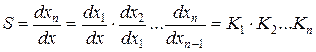 , (12.1)
, (12.1)
где 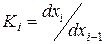 – коэффициент преобразования i-го звена.
– коэффициент преобразования i-го звена.
Под действием внешних факторов коэффициенты 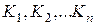 могут
могут
меняться на величину 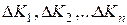 . Изменение коэффициентов преобразования означает изменение чувствительности. Если эти изменения коэффициентов Кi достаточно малы, то членами второго и большего порядка малости можно пренебречь. Тогда относительное изменение чувствительности можно определить выражением
. Изменение коэффициентов преобразования означает изменение чувствительности. Если эти изменения коэффициентов Кi достаточно малы, то членами второго и большего порядка малости можно пренебречь. Тогда относительное изменение чувствительности можно определить выражением
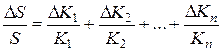 . (12.2)
. (12.2)
Изменение чувствительности приводит к изменению выходного сигнала на величину
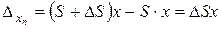 .
.
Это означает, что значение входной величины х, определяемое по значению выходной хn, будет измерено с погрешностью. Абсолютная величина погрешности измерения – ∆х определяется отношением:
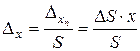 . (12.3)
. (12.3)
Очевидно, что погрешность (12.3), вызванная изменением чувствительности, является мультипликативной.
Аддитивная погрешность средств по схеме рис. 12.1 вызывается дрейфом нуля звеньев, а также наложением помех на полезный сигнал. Эти воздействия приводят к смещению графика характеристики преобразования i-го звена (см. рис. 12.2) на величину 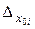 . Чтобы найти аддитивную погрешность, в схему рис. 12.1 вводят дополнительные, внешние сигналы –
. Чтобы найти аддитивную погрешность, в схему рис. 12.1 вводят дополнительные, внешние сигналы – 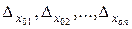 . Результирующее действие этих сигналов равно действию одного дополнительного сигнала
. Результирующее действие этих сигналов равно действию одного дополнительного сигнала 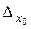 на входе схемы, причем
на входе схемы, причем
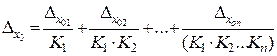 . (12.4)
. (12.4)

Значение 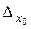 определяет результирующую аддитивную погрешность. Таким образом, в средствах измерений, имеющих структурную схему прямого преобразования, происходит суммирование погрешностей всех звеньев. Это затрудняет изготовление средств прямого преобразования с высокой точностью.
определяет результирующую аддитивную погрешность. Таким образом, в средствах измерений, имеющих структурную схему прямого преобразования, происходит суммирование погрешностей всех звеньев. Это затрудняет изготовление средств прямого преобразования с высокой точностью.
1.2 Средства измерений уравновешивающего
преобразования.
Структурная схема средства уравновешивающего преобразования приведена на рис. 12.3. На этом рисунке ПОС1,2…,m – звенья цепи обратной связи (ЦОС) с коэффициентами преобразования 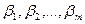 . Поэтому
. Поэтому
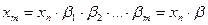 . (12.5)
. (12.5)
На входе цепи прямого преобразования, в сравнивающем узле (СУ), происходит сравнение (компенсация) входного сигнала х и сигнала ЦОС –
хm. На выходе СУ получаем разностный сигнал
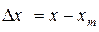 .
.
Средства измерений уравновешивающего преобразования могут работать как с полной компенсацией, так и с неполной.
При полной компенсации в установившемся режиме
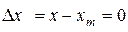 . (12.6)
. (12.6)
Это возможно в тех устройствах, у которых в цепи прямого преобразования есть интегрирующее звено с характеристикой
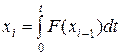 .
.
Такую характеристику имеет следящий двигатель. Угол поворота вала такого двигателя пропорционален напряжению и времени. Тогда, учитывая (12.5) и (12.6), можно записать
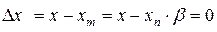 ,
,
а
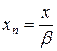 . (12.7)
. (12.7)
Выражение (12.7) показывает, что сигнал на выходе средства измерения хn пропорционален входному и не зависит от коэффициентов цепи прямого преобразования.
Поэтому чувствительность средства определится выражением:
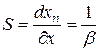 . (12.8)
. (12.8)
Мультипликативная относительная погрешность, обусловленная нестабильностью коэффициентов преобразования звеньев, равна отношению отрицательного приращения ∆β к значению β:
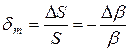 (12.9)
(12.9)
и имеет только отрицательный знак.
Аддитивная погрешность схемы рис. 12.3 обуславливается порогом чувствительности звеньев (наименьшим изменением входного сигнала, которое способно вызвать появление сигнала на выходе). Характеристика преобразования такого звена приведена на рис. 12.4.
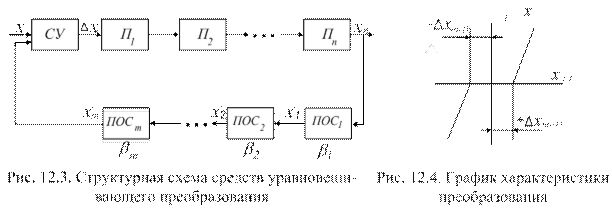
При наличии порога чувствительности состояние компенсации наступает, когда
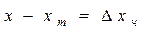 ,
,
причем
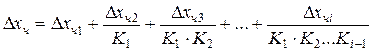 .
.
Таким образом, изменение входного сигнала в пределах 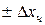 не вызывает изменений выходного сигнала, т.е. появляется абсолютная аддитивная погрешность.
не вызывает изменений выходного сигнала, т.е. появляется абсолютная аддитивная погрешность.
При неполной компенсации выходной сигнал
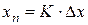 . (12.10)
. (12.10)
В этом случае установившийся режим наступает при некоторой разности
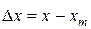 . (12.11)
. (12.11)
Зависимость между выходным и входным сигналами можно найти, применяя к (12.10) выражения (12.5), и (12.11). Тогда (12.10) принимает вид
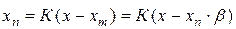 .
.
Решая последнее выражение относительно хn , получим
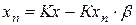
или
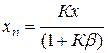 . (12.12)
. (12.12)
Отсюда следует, что чувствительность средства измерения уравновешивающего преобразования при неполной компенсации определяется выражением
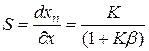 . (12.13)
. (12.13)
Относительное изменение чувствительности, или мультипликативная погрешность, имеет вид
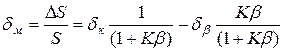 , (12.14)
, (12.14)
где: 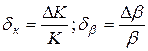 .
.
Если 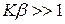 , то выражение (12.14) приходит к виду
, то выражение (12.14) приходит к виду
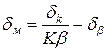 ,
,
т.е. и при неполной компенсации мультипликативная погрешность существенно ослабляются.
Аддитивная помеха может быть найдена введением в структурную схему дополнительных сигналов 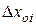 , определяющих смещение характеристик
, определяющих смещение характеристик
преобразования соответствующих звеньев.
2. СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ
РЕЖИМЕ
В динамическом режиме точность измерений зависит от динамических свойств средств и от характера изменения измеряемой величины. Реальные средства измерений обладают динамическими (инерционными) свойствами из-за наличия элементов запасающих энергию, например, емкостей, индуктивностей, упругих элементов в электромеханических приборах.
Для описания динамических свойств измерительных приборов и оценки их погрешностей в динамическом режиме применяются различные способы. Наиболее полно эти свойства могут быть описаны дифференциальными уравнениями, переходными и импульсными переходными характеристиками, частотными характеристиками и передаточными функциями. Рассмотрим применение для этих целей частотных характеристик.
Спектральная форма представления наглядно показывает, что спектр реальных сигналов занимает некоторую полосу частот. Средства измерений характеризуются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками.
Под АЧХ понимают зависимость от частоты модуля коэффициента передачи измерителя, а под ФЧХ – зависимость от частоты аргумента 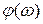 (разность фаз выходного и входного сигналов).
(разность фаз выходного и входного сигналов).
Обозначим коэффициент передачи измерителя отношением
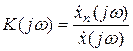 .
.
Тогда АЧХ идеального средства измерения определяется отношением номинальных значений этих величин и постоянна на всей оси частот
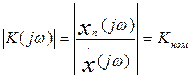 ,
,
а ФЧХ равна нулю
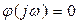 ,
,
где Кном – номинальный коэффициент преобразования.
Для реального звена первого порядка
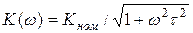 , (12.15)
, (12.15)
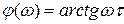 , (12.16)
, (12.16)
где 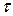 - постоянная времени звена, причем
- постоянная времени звена, причем 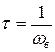 ,
, 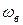 - верхняя граничная частота АЧХ.
- верхняя граничная частота АЧХ.
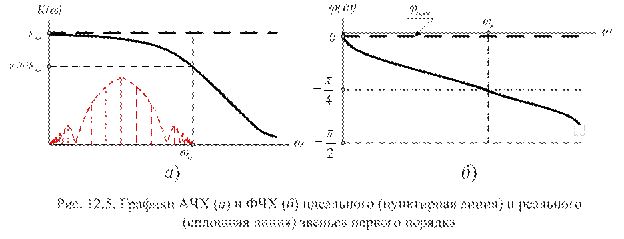
Графики АЧХ и ФЧХ, построенные по (12.15) и (12.16) приведены на рис. 12.5 (сплошная линия). Пунктирной линией показаны графики идеальных средств. График АЧХ совмещен со спектром измеряемого сигнала.
Рассмотрим возможность оценки динамических погрешностей по известным АЧХ и ФЧХ средств измерений. Пусть оценке подлежит сигнал 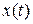 . Пусть также амплитуда сигнала изменяется в диапазоне от
. Пусть также амплитуда сигнала изменяется в диапазоне от 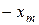 до
до 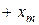 , а частота – в диапазоне от 0 до ωв. Предположим, что средство измерений имеет АЧХ и ФЧХ первого порядка (рис. 12.5).
, а частота – в диапазоне от 0 до ωв. Предположим, что средство измерений имеет АЧХ и ФЧХ первого порядка (рис. 12.5).
Сначала оценим влияние на динамическую погрешность только АЧХ.
Условно примем 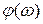 = 0. Реальная АЧХ в пределах полосы пропускания изменяется от КНОМ до 0,707КНОМ. Поэтому каждая i-я спектральная составляющая сигнала передается с
= 0. Реальная АЧХ в пределах полосы пропускания изменяется от КНОМ до 0,707КНОМ. Поэтому каждая i-я спектральная составляющая сигнала передается с 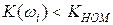 . Это приводит к искажению
. Это приводит к искажению 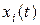 , а значит, к появлению погрешности. Для каждой гармонической составляющей
, а значит, к появлению погрешности. Для каждой гармонической составляющей 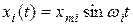 относительная погрешность определится выражением
относительная погрешность определится выражением
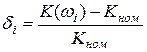 . (12.17)
. (12.17)
Теперь рассмотрим влияние ФЧХ. Примем условно 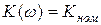 во всем диапазоне рассматриваемых частот. Пусть на входе звена действует сигнал
во всем диапазоне рассматриваемых частот. Пусть на входе звена действует сигнал 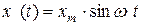 . Если звено идеальное, то его реакция имеет вид:
. Если звено идеальное, то его реакция имеет вид:
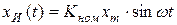 .
.
Реакция реального звена имеет вид:
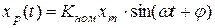 .
.
Погрешность определим как разность реакций:
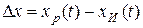 .
.
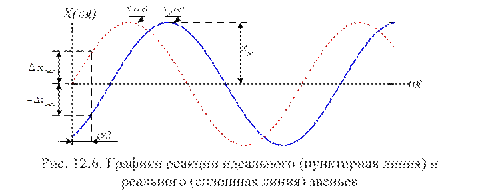
Очевидно, что величина погрешности определяется фазовым сдвигом.
Это наглядно иллюстрируют графики рис. 12.6. Как видно по рис. 12.6 реакция отстает от воздействия. При 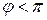 погрешность максимальна для значения
погрешность максимальна для значения 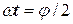 . Поэтому выражение для оценки максимальной погрешности примет вид:
. Поэтому выражение для оценки максимальной погрешности примет вид:
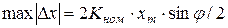 .
.
Если 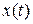 представляет собой сумму N гармонических составляющих
представляет собой сумму N гармонических составляющих 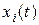 , то максимально возможная погрешность также определится суммой
, то максимально возможная погрешность также определится суммой
погрешностей гармоник:
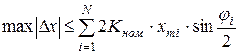 . (12.18)
. (12.18)
В общем случае на динамическую погрешность влияет как АЧХ, так и ФЧХ каждого звена. Точное определение суммарной погрешности – сложная задача. В качестве оценки сверху принимают сумму двух составляющих. Но нужно помнить, что это достаточно грубая оценка.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
12.1. Почему значение погрешности средств измерений зависит от режима их работы?
12.2. Сформулируйте условия, при которых средства измерений работают в статическом режиме.
12.3. Приведите примеры известных вам измерительных приборов, имеющих структурную схему прямого преобразования.
12.4. Приведите определение мультипликативной погрешности средств прямого преобразования.
12.5. При измерении постоянного напряжения 40 В магнитоэлектрическим измерительным прибором, имеющим нормированное значение шкалы 50 В и цену деления 0,5 В / дел, была обнаружена абсолютная погрешность прибора 0,6 В. Определите абсолютное значение приращения чувствительности ∆S за счет дестабилизирующих факторов, а также значение мультипликативной погрешности.
12.6. Перечислите основные причины аддитивных погрешностей средств прямого преобразования.
12.7. При каком значении коэффициента передачи средств прямого преобразования К вклад в аддитивную погрешность звеньев тем меньше, чем больше их номер?
12.8. При каких условиях средства измерения уравновешивающего преобразования могут работать с полной компенсацией?
12.9. Сравните чувствительность средств уравновешивающего преобразования с полной и неполной компенсацией. Определите условия, при которых чувствительность средств становится практически одинаковой.
12.10. Сформулируйте условия, при которых средства измерений переходят в динамический режим работы.
12.11. Какие свойства сигналов и средств измерений позволяют оценить динамические погрешности по частотным характеристикам средств?
Дата добавления: 2020-10-14; просмотров: 812;











