Предельная ошибка выборки

Полученные показатели генеральной совокупности по средством выше указанных формул, можно гарантировать лишь с определенной доле вероятности. В математической статистике доказано, что пределы значений генеральной совокупности отличаются от показателей выборочной совокупности на величину средней ошибки выборки лишь с вероятностью 0,683. Это значит, что в 683 случаях из 1000 значения генеральной совокупности будут находиться в установленных пределах, а в остальных 317 они могут выйти за эти пределы. Но вероятность можно повысить, если расширить пределы отклонений. Для этого средняя ошибка выборки увеличивается в t раз. Коэффициент t называется коэффициентом доверия. Он определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного обследования.

Установлено, что при t = 1, вероятность равна 0,683 (68,3 %);

при t = 2, вероятность равна 0,954 (95,4 %); при t = 3, вероятность равна 0,997 (99,7 %).

Средняя ошибка выборки, умноженная на коэффициент доверия, называется предельной ошибкой выборки.

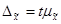(6.9.)

Зная выборочную среднюю величину признака ( 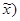и предельную ошибку выборки ( 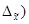, можно определить границы (пределы), в которых заключена генеральная средняя:

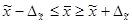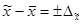или (6.10.)

Зная выборочную долю признака (w) и предельную ошибку выборки ( 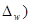, можно определить границы, в которых заключена генеральная доля (р):

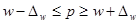(6.11.)